高一数学第一学期期中质量调研
高一数学（必修1） 试题
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 1-10 | 11-16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得分 | |||||||||
| 得分 | 评卷人 |
一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将你认为正确的答案填在下面的表格中．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
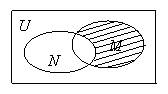1．右图中矩形表示全集
，两个椭圆分别表示集合
、
，则阴影部分所表示的集合为
．
．
．
．
2．设
，
，
，则
，
，
的大小关系为
．
．
．
．
3．设集合
，若
：
是集合到集合的映射，则集合可以是
.
.
.
. 
4．对于定义在
上的函数
，下列结论正确的是
．若
，则函数是偶函数；
．若
，则函数不是偶函数；
．若，则函数不是奇函数；
．若
，则函数在上是单调增函数
5．设函数
，
，则这两个函数图象之间的关系是
．关于
轴对称
．关于
轴对称
．关于直线
对称
．关于原点对称
6．某市出租车收费标准如下：在
以内（含）路程按起步价5元收费，超过以外的路程按2元
收费（注：超过以外的路程按1
为单位计算路程，不足1的部分按1计算）．若某人乘坐一次出租车付费15元，则出租车行驶的路程（）所在的区间是
．
．
．
．
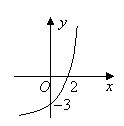7．已知函数
（
且
）的图象如图所示，则，的值分别是
．
，
．， 
．
，
．，
8．函数
，
的值域是
．
．
．
．
9．设函数
的两个零点为
，
，且
，则，所在的区间是
．
，
． 
，
．，
．
，
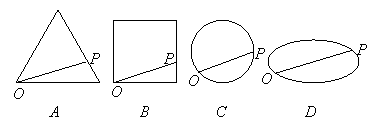
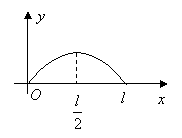10．点
从点
出发，按逆时针方向沿周长为
的图形运动一周，、两点连线的长与点走过的路程的函数关系如右图，那么点所走的图形是
 |
| 得分 | 评卷人 |
二、填空题：本大题共6小题，每小题4分，共24分．把答案直接填在题中横线上．
11．
；
12．函数
的定义域是
；
13．已知集合
，
，若
，则的取值范围是
；
14．已知函数和
的定值域都是集合，其中
，
，
；
，
．则方程
的解集为
；
15．如果在函数
的图象上任取不同的两点、，线段
（端点除外）总在图象的下方，那么函数的图象给我们向上凸起的印象，我们称函数为上凸函数；反之，如果在函数的图象上任取不同的两点、，线段（端点除外）总在图象的上方，那么我们称函数为下凸函数．例如：
就是一个上凸函数．请写出两个不同类型的下凸函数的解析式：
；
16．期中考试，某班数学优秀率为
，语文优秀率为
，英语优秀率为
，则上述三门学科都优秀的百分率至少为
．
| |
| 得分 | 评卷人 |
17．（本小题满分10分）
根据下列条件求值：
（Ⅰ）已知
，
，求
的值；
（Ⅱ）已知
，求
的值．
| 得分 | 评卷人 |
18．（本小题满分10分）
解下列方程：
（Ⅰ）
；
（Ⅱ）
．
| 得分 | 评卷人 |
19．（本小题满分10分）
已知函数
，
．
（Ⅰ）用函数单调性的定义证明：在其定义域上是单调增函数；
（Ⅱ）若
，求的取值范围．
| 得分 | 评卷人 |
20．（本小题满分11分）
已知函数
，
（，且）．
（Ⅰ）求函数
的定义域；
（Ⅱ）求使函数的值为正数的的取值范围．
| 得分 | 评卷人 |
21．（本小题满分12分）
设为实数，函数
，
．
（Ⅰ）若是偶函数，试求的值；
（Ⅱ）在（Ⅰ）的条件下，求的最小值；
（Ⅲ）王强同学认为：无论取何实数，函数都不可能是奇函数．
你同意他的观点吗？请说明理由．
| 得分 | 评卷人 |
22．（本小题满分13分）
在经济学中，函数的边际函数
定义为
．某公司每月最多生产100台报警系统装置，生产台（
）的收入函数为
（单位：元），其成本函数为
（单位：元），利润是收入与成本之差．
（Ⅰ）求利润函数
及边际利润函数
的解析式，并指出它们的定义域；
（Ⅱ）利润函数与边际利润函数是否具有相同的最大值？说明理由；
（Ⅲ）解释边际利润函数的实际意义．
江苏省溧阳市2007~2008学年度第一学期期中质量调研
高一数学（必修1）参考答案（07.11）
一、选择题：（共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | D | B | A | C | B | D | C | C |
二、填空题：（共24分）
11.
1
12. 
13.
14. 
15.
，
16. 25
三、解答题：（共66分）
17. 解：（Ⅰ）∵
，
，
∴
……………2分
；
……………4分
……………5分
（Ⅱ）（法一）
由 
，得 
，
……………6分
∴ 
，
……………8分
∴ 
．
……………10分
（法一）
∵，∴
，
……………8分
∴
．
……………10分
18. 解：（Ⅰ）原方程可化为 
，
即
，
……………3分
∴ 
，
即 
，
解得
．
……………5分
（Ⅱ）原方程可化为 ，
，
……………7分
即 
，
解得 
，
，
……………9分
经检验，原方程的解为
．
……………10分
19. 证明：（Ⅰ）设
，则
……………1分
，
……………3分
∵
，
∴
，
，
……………4分
∴
，即
，
……………5分
所以，在
上是单调增函数．
……………6分
或 由 
∵
，
∴ ，，
∴
，
∴，即，
……………5分
所以，在上是单调增函数．
……………6分
（Ⅱ）∵在其定义域上是单调增函数，
∴由
得 
，
……………8分
即
，
∵
是增函数，∴
，
……………9分
解得
，即的取值范围是
．
……………10分
20. 解：（Ⅰ）由题意可知，
，
……………1分
由
， 解得 
，
……………3分
∴
，
……………4分
∴函数的定义域是
．
……………5分
（Ⅱ）由
，得 
，
即 
， ①
……………6分
当
时，由①可得 
，解得
，
又，∴
； ……………8分
当
时，由①可得 
，解得
，
又，∴
．
……………10分
综上所述：当时，的取值范围是
；
当时，的取值范围是
． ……………11分
21.解：（Ⅰ）∵是偶函数，∴
在上恒成立，
即
，
……………1分
化简整理，得 
在上恒成立，
……………3分
∴
．
……………4分
或由是偶函数知，
即 
整理得
，解得 ……………2分
再证明
是偶函数，所以 ……………4分
（Ⅱ）由（Ⅰ）知，∴，
……………5分
∵
，
，∴
，当且仅当
时，
，…………7分
∴当时，的最小值为1．
……………8分
（Ⅲ）王强同学的观点是正确的． ……………9分
若是奇函数，则
在上恒成立，
∴
，∴
，
……………10分
但无论取何实数，
，
∴不可能是奇函数．
……………12分
22. 解（Ⅰ）由题意知：
，
……………2分
其定义域为
，且；
……………3分
，
……………5分
其定义域为，且．
……………6分
（Ⅱ）
，
∴当
或
时，的最大值为
元．
……………8分
∵
是减函数，
∴当
时，的最大值为
元．
……………10分
∴利润函数与边际利润函数不具有相同的最大值． …………11分
（Ⅲ）边际利润函数的实际意义是：生产第
台报警系统装置的利润是（
）元．
…………13分