高一数学第一学期期末考试
高一数学《必修1》与《选修2-2》学分认定考试试题
命题人: 高一数学备课小组 审阅人:梁金星
一、选择题:(本大题共8小题,每题4分,每小题均只有一个正确答案,满分32分)
1.二次函数![]() ,的顶点坐标为( B )
,的顶点坐标为( B )
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.已知函数![]() ,
,![]() ,则
,则![]() 的值域为( D )
的值域为( D )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]()
3. 下列图象是函数![]() 的导函数
的导函数![]() 的图象,满足
的图象,满足![]() 是函数f(x)的极小值的是( B )
是函数f(x)的极小值的是( B )
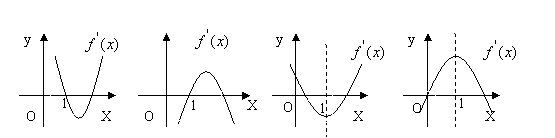
A B C D
4. 已知函数![]() 的图象是连续不断的,有如下的
的图象是连续不断的,有如下的![]() ,
,![]() 对应值表:
对应值表:
|
| 1 | 2 | 3 | 4 | 5 | 6 |
|
| 123.56 | 21.45 | -7.82 | 11.57 | -53.76 | -126.49 |
函数在区间[1,6]上的零点至少有( C )个
![]()
![]()
![]()
![]()
5.函数y=log2x+1的图象是( C )
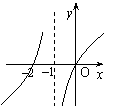
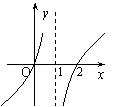 | 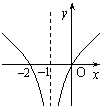 | ||||
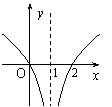 | |||||
A. B. C. D.
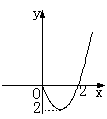
6.已知f(x)为偶函数,当x>0时的图象为抛物线的一部分(如图),则当x<0时f(x)= (A)
A.2x2+4x B. x2+2x C. 2x2–4x D. x2–2x
7.![]() ,
,![]() ,
,![]() 三个数的大小关系是( A )
三个数的大小关系是( A )
A.![]() <
<![]() <
<![]() B.
B.![]() <
<![]() <
<![]()
C.![]() <
<![]() <
< ![]() D.
D.![]() <
<![]() <
<![]()
8.函数f(x)的定义域为R,对于任意的x∈R,恒有![]() ,
,![]() ,则在[0,10]内方程
,则在[0,10]内方程![]() 的解至少有(B)
的解至少有(B)
A.4个 B.5个 C.6 个 D.7个
二、填空题:(本大题共5小题,每题4分,共20分)
9.曲线![]() 在
在![]() 处的切线斜率是
2
处的切线斜率是
2
10.已知直线![]() 经过点
经过点![]() 且在
且在![]() 轴上的截距为1,则直线
轴上的截距为1,则直线![]() 的方程为:
的方程为:![]()
11.一次函数y=2x+4的图象与两坐标轴围成的三角形的面积为 (平方单位) 4
12.如果函数![]() 在区间D上是凸函数,则对区间D上的任意
在区间D上是凸函数,则对区间D上的任意![]() ,都有
,都有![]() .下面函数中:
.下面函数中:
1![]() ,;2
,;2![]() , 3
, 3![]() 4
4![]()
在其定义域内是凸函数的有 (填入序号)2 4
13.定义在R上的函数y=f(x)为奇函数,在![]() 上是减函数且
上是减函数且![]() ,则
,则![]() 的解集为
. 答案:
的解集为
. 答案:![]() ;
;
三、解答题:(本大题共6小题,共48分,解答应写出文字说明、证明过程或演算步骤)
14.(本小题满分7分)
求解关于x的不等式的解集:
![]()
解: ![]()
15.(本小题满分7分)
已知函数![]() ,
,
(Ⅰ)求函数![]() 的定义域、单调递增区间;
的定义域、单调递增区间;
(Ⅱ)求函数![]() 的值域.
的值域.
答案: (Ⅰ)定义域![]() ;递增区间为
;递增区间为![]()
(Ⅱ)值域为![]()
16.(本小题满分8分)
已知![]() 是R上的单调函数,且对任意的实数
是R上的单调函数,且对任意的实数![]() ,有
,有![]() 恒成立,若
恒成立,若![]()
(Ⅰ)求![]()
(Ⅱ)判断![]() 是R上的增函数还是减函数(只要写出结果,不必证明),并解关于
是R上的增函数还是减函数(只要写出结果,不必证明),并解关于![]() 的不等式:
的不等式:![]()
证明:(1)令![]()
(2)由![]() 是R上的奇函数,
是R上的奇函数,![]() ,又因
,又因![]() 是R上的单调函数,
是R上的单调函数,
由![]() ,所以
,所以![]() 为R上的减函数.
为R上的减函数.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
当![]() 时,
时,![]() .
.
17.(本小题满分8分)
已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且方程
,且方程![]() 的两个实根为
的两个实根为![]()
(Ⅰ)若![]() ,求
,求![]() 的解析式;
的解析式;
(Ⅱ)若函数![]() 无极值,求实数
无极值,求实数![]() 的取值范围
的取值范围![]()
解:⑴设![]()
![]() ,又
,又![]()
![]() …………(2分)
…………(2分)
故![]() 的解析式
的解析式![]() ……………3分
……………3分
⑵∴![]() ……… ①
……… ① ![]() ……… ②
……… ②
由①②得![]() ,∴
,∴![]() ,
,
![]() …………………………………………(5分)
…………………………………………(5分)
∵![]() 无极值,∴方程
无极值,∴方程![]() …………(6分)
…………(6分)
则
![]() ,解得
,解得![]() ………………(7分)
………………(7分)
故实数![]() 的取值范围为
的取值范围为![]() ………………………………………………(8分)
………………………………………………(8分)
18.(本题满分8分)
某工厂有216名工人接受了生产1000台W型高科技产品的总任务,已知每台W型产品由4个W-1型装置和3个W-2型装置装配组成,每名工人每小时能加工6个人W-1型装置或3个W-2型装置,现将工人分成两组同时开始加工,每组分别加工一种装置.设加工W-1型装置的工人有![]() 人,他们加工完成W-1型装置所需时间为
人,他们加工完成W-1型装置所需时间为![]() ,其余工人加工完成W-2型装置所需时间为
,其余工人加工完成W-2型装置所需时间为![]() (单位:小时)
(单位:小时)
(Ⅰ)写出![]() 、
、![]() 的解析式;
的解析式;
(Ⅱ)比较![]() 与
与![]() 的大小,并写出这216名工人完成总任务的时间
的大小,并写出这216名工人完成总任务的时间![]() 的解析式;
的解析式;
(Ⅲ)问应怎样分组,才能使完成总任务的用时最少?
解:(1)由题意可知,需加工W-1型装置4000个,加工W-2型装置3000个,所用工人分别为![]() 人,216
人,216![]() 人
人
所以![]() ,
,![]() (
(![]() )
)
(2)![]()
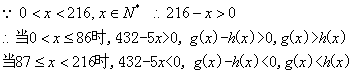
所以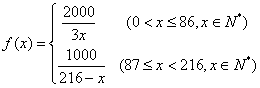
(3)完成总任务时间最少,即求![]() 的最小值
的最小值
![]() ,
,![]() 递增
递增
所以![]() ,
,![]() ,这时
,这时![]()
![]() ,
,![]() 递减
递减
所以![]() ,
,![]() ,这时
,这时![]()
所以加工W-1型装置和加工W-2型装置的人数分别为86和130,87和129.
19.(本小题满分10分)
设![]() 是定义在
是定义在![]() 上的奇函数,且当
上的奇函数,且当![]() 时,
时, ![]()
![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ) 当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值
上的最大值![]() ;
;
(Ⅲ)如果对满足![]() 的一切实数
的一切实数![]() ,函数
,函数![]() 在
在![]() 上恒有
上恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解: (Ⅰ)当![]() 时,
时, ![]() ,则
,则
![]()
![]() .
……………………………1分
.
……………………………1分
当![]() 时,
时, ![]()
![]() .
.
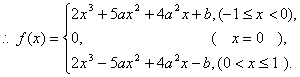 …………………………2分
…………………………2分
(Ⅱ)当![]() 时
时
![]()
![]()
![]() .
………3分
.
………3分
(1)当![]() ,即
,即![]() 时
时
当![]() 时,
时,![]() , 当
, 当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减,
上单调递减,
![]() .
……………………………4分
.
……………………………4分
(2)当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增.
单调递增.
![]() ,
……………………………5分
,
……………………………5分
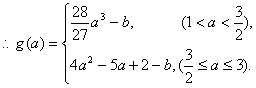 ……………………………6分
……………………………6分
(Ⅲ) 要使函数![]() 在
在![]() 上恒有
上恒有![]() ,必须使
,必须使![]() 在
在![]() 上的最大值
上的最大值![]() .
.
也即是对满足![]() 的实数
的实数![]() ,
,![]() 的最大值要小于或等于
的最大值要小于或等于![]() .
.
(1)当![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上是增函数,
上是增函数,
则![]()
![]()
![]() .
.
![]() ,解得
,解得![]() . ………①
……………………………7分
. ………①
……………………………7分
(2)当![]() 时,
时,![]()
此时,![]() 在
在![]() 上是增函数,
上是增函数, ![]() 的最大值是
的最大值是![]() .
.
![]() ,解得
,解得![]() .………②
……………………………8分
.………②
……………………………8分
由①、②得实数![]() 的取值范围是
的取值范围是![]() .
……………………………9分
.
……………………………9分