高一数学第一学期期末联考试题
(考试时间:120分钟 总分160分)
命题人:丁荣康( 江苏省黄桥中学) 张圣官( 江苏省姜堰中学) 韦 伟( 江苏省兴化中学)
审题人:窦如强(姜堰市教研室) 石志群(泰州教研室) 蔡德华(泰兴第二高级中学)
参考公式:S球=4![]() V锥体=
V锥体=![]() V台体=
V台体=
![]()
注意事项:
所有试题的答案均填写在答题纸上,答案写在试卷上的无效.
一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)
1.如果全集![]() ,A={2,5,8},
,A={2,5,8},![]() ,那么(
,那么(![]() )
)![]() 等
等
于 ▲ .
2.过点(-1,3)且垂直于直线x - 2y + 3=0的直线方程为 ▲ .
3.已知:两个函数f(x)和g(x)的定义域和值域都是{1,2,3},其定义如下表:
| x | 1 | 2 | 3 | x | 1 | 2 | 3 | |
| f(x) | 2 | 3 | 1 | g(x) | 1 | 3 | 2 |
则g[f(1)],g[f(2)],g[f(3)]的值依次为. ▲ .
4.边长为2的正方体的内切球的表面积为 ▲ .
5.设![]() {-1,1,
{-1,1,![]() ,3},则使幂函数
,3},则使幂函数![]() 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有![]() 的值为
的值为
▲ .
6.已知函数f(x)为偶函数,当![]() 时,f(x)=x-1,则满足f(x)<0的实数x的取值范围是 ▲ .
时,f(x)=x-1,则满足f(x)<0的实数x的取值范围是 ▲ .
7.AB、CD是两条异面直线,则直线AC、BD的位置关系一定是__▲_(填“平行”、“相交”或“异面”).
8.直线ax+y-a=0与圆x2+y2=4的位置关系是 ▲ .
9.一个几何体的俯视图是两个半径分别为2和4的同心圆,主视图是一个上底为4,下底为8,腰为![]() 的等腰梯形,则它的体积为 ▲ .
的等腰梯形,则它的体积为 ▲ .
10.已知点A(1,-2,1),B(2,2,2),点P在Z轴上,且PA=PB,则点P的坐标为 ▲ .
11.设m、n是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④若![]() ,则
,则![]() ;
;
其中正确命题的序号是 ▲ .
12.计算![]() ▲
.
▲
.
13.某同学在借助计算器求“方程lgx=2-x的近似解(精确到0.1)”时,设f(x)=lgx+x-2, 算得f(1)<0,f(2)>0;在以下过程中,他用“二分法”又取了x的4个不同值,计算了其函数值的正负,并得出判断:方程的近似解是x≈1.8.那么他又取的x的4个不同值中的前两个值依次为 ▲ .
14.过点(-4,0)作直线l与圆x2+y2+2x-4y-20=0交于A、B两点,如果AB=8,则直线l的方程为 ▲ .
二、解答题:(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分14分)
设A={x2x2+ax+2=0}, 2![]() A.
A.
(1) 求a的值,并写出集合A的所有子集;
(2) 已知B={2,-5},设全集![]() A
A![]() B,求
B,求![]() .
.
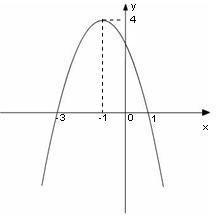
16.(本小题满分15 分)
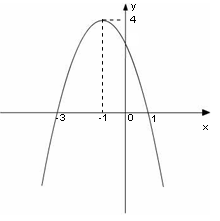
右图是一个二次函数y=f(x)的图象.
(1)写出这个二次函数的零点;
(2)求这个二次函数的解析式;
(3)当实数k在何范围内变化时,
g(x)=f(x)-kx在区间 [-2,2]上是单调函数.
17.(本小题满分14 分)
在直角坐标系中,已知射线OA:x-y=0(x![]() 0),OB:x+
0),OB:x+![]() y=0(x
y=0(x![]() 0),过点P(1,0)作直线分别交射线OA,OB于A,B点.
0),过点P(1,0)作直线分别交射线OA,OB于A,B点.
(1)当AB中点为P时,求直线AB的方程;
(2)在(1)的条件下,若A、B两点到直线l:y=mx+2的距离相等,求实数m的值.
18.(本小题满分 14 分)
我市有甲,乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同.甲俱乐部每张球台每小时5元;乙俱乐部按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.小张准备下个月从这两家俱乐部中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.
(1)设在甲俱乐部租一张球台开展活动x小时的收费为f(x)元(15![]() 40),在乙俱乐部租一张球台开展活动x小时的收费为g(x)元(15
40),在乙俱乐部租一张球台开展活动x小时的收费为g(x)元(15![]() 40),试求f(x)和g(x);
40),试求f(x)和g(x);
(2)你认为小张选择哪家俱乐部比较合算?请说明理由.
19.(本小题满分16 分)
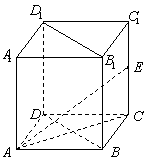
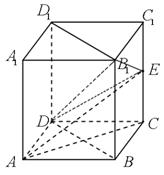 在正方体ABCD-A1B1C1D1中, AA1=2,E为棱CC1的中点.
在正方体ABCD-A1B1C1D1中, AA1=2,E为棱CC1的中点.
(1) 求三棱锥E-ABD的体积;
(2) 求证:B1D1![]() AE;
AE;
(3) 求证:AC//平面B1DE.
20.(本小题满分 17 分)
已知圆![]() 过原点
过原点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]()
![]() .
.
(1) 求圆![]() 的方程;
的方程;
(2) 过原点![]() 作射线交圆
作射线交圆![]() 于另一点
于另一点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①![]() 是否存在最小值?若存在,求出最小值;若不存在,请说明理由;
是否存在最小值?若存在,求出最小值;若不存在,请说明理由;
②若射线![]() 上一点
上一点![]() 满足
满足![]() ,求证:
,求证:
![]() .
.
 |
|
|

| 题号 | 一 | 二 | 总分 | 初计分 | 复计分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | |||||
| 得分 | ||||||||||

| 得分 | 初评卷人 | 复评卷人 |
一、填空题(本大题共14小题,每小题5分,共70分,
把答案填在下面的横线上。)
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. 11. 12.
13. 14.
二、解答题(本大题共6小题,合计90分,解答应写出文字说明,证明过程或演算
步骤)
| 得分 | 初评卷人 | 复评卷人 |
15、 (本大题共14分)
 请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效

| 得分 | 初评卷人 | 复评卷人 |
16、 (本大题共15分)
 请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效

| 得分 | 初评卷人 | 复评卷人 |
17、 (本大题共14分)
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效

| 得分 | 初评卷人 | 复评卷人 |
18、 (本大题共14分)

请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效

| 得分 | 初评卷人 | 复评卷人 |
 19、 (本大题共16分)
19、 (本大题共16分)

请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效

| 得分 | 初评卷人 | 复评卷人 |
20、 (本大题共17分)
高一数学试题参考答案
一、填空题:(本大题共14小题,每小题5分,共70分.)
1.{1,3,7} 2.2x+y-1=0 3.3、2、1 (不按顺序依次填写算错)
4.4![]() 5.1、3
6.(-1,1)
5.1、3
6.(-1,1)
7.异面
8.相交
9.14![]()
10.(0,0,3) 11.①②③ 12.![]()
13.1.5、1.75 14.x= - 4或5x+12y+20=0
二、解答题:(本大题共6小题,共90分.)
15.(本小题满分14分)
解:(1)![]()
![]()
![]() ---------------4’
---------------4’
![]() ,解得
,解得![]()
A={2,![]() }
}
A的子集为![]() ,{2},{
,{2},{![]() },{2,
},{2,![]() }
---------------8’
}
---------------8’
(2) ![]() ={2,
={2,![]() ,-5}
---------------11’
,-5}
---------------11’
![]() ={
={![]() ,-5}
---------------14’
,-5}
---------------14’
16.(本小题满分15分)
解:(1)由图可知二次函数的零点为-3,1 ---------------4’
(2)设二次函数为y=a(x+3)(x-1),点(-1,4)在函数上,解得a=-1
y=-(x+3)(x-1)= -x2-2x+3. ---------------9’
(3)g(x)=-x2-2x+3-kx=
-x2-(k+2)x+3,开口向下,对称轴为x= -![]()
当-![]() ,即k
,即k![]() 2时,g(x)在[-2,2]上递减--------------12’
2时,g(x)在[-2,2]上递减--------------12’
当-![]() , 即k
, 即k![]() -6时,g(x)在[-2,2]上递增
-6时,g(x)在[-2,2]上递增
综上所述k![]() -6或 k
-6或 k![]() 2
---------------15’
2
---------------15’
注:第(1)小题中若零点写为(-3,0)、(1,0),扣2分。
17.(本小题满分14分)
解:(1)设A(a,a), ![]() A、B的中点为P,
A、B的中点为P,![]() B(2-a,-a)
B(2-a,-a)
![]() (2-a)+3(-a)=0,解得a=
(2-a)+3(-a)=0,解得a=![]() ,
,
A(![]() ,
,![]() ),B(
),B(![]() )
)
直线AB为y=(-1-![]() )(x-1) ---------------7’
)(x-1) ---------------7’
(2)解法一:若A、B两点到直线l:y=mx+2的距离相等,
![]() 直线l与直线AB平行或过A、B中点 ---------------11’
直线l与直线AB平行或过A、B中点 ---------------11’
![]() m=-1-
m=-1-![]() 或m=-2
--------------14’
或m=-2
--------------14’
解法二:由A、B两点到l:mx-y+2=0距离相等
得![]() =
=![]() -----------11’
-----------11’
![]() m=-1-
m=-1-![]() 或m=-2
--------------14’
或m=-2
--------------14’
18.(本小题满分14分)
解:(1)![]() ,
,![]() --------------3’
--------------3’
![]() -----------7’
-----------7’
(2)①若15≤x≤30,当5x=90时,x=18
即当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
当18<x≤30时,![]() 。
-------------10’
。
-------------10’
②若30<x≤40,5x>30+2x恒成立,即![]() 恒成立 ------------12’
恒成立 ------------12’
综上所述:当![]() 时,小张选甲俱乐部比较合算,
时,小张选甲俱乐部比较合算,
当![]() 时,两家一样合算,
时,两家一样合算,
当![]() 时,选乙家比较合算。
--------------14’
时,选乙家比较合算。
--------------14’
19.(本小题满分16分)
解:(1)![]() 平面ABD,
平面ABD,
∴V=![]() CE.SABD=
CE.SABD=![]() --------------4’
--------------4’
(2)连结A1C1,在正方体![]() 中
中
B1D1![]() A1C1,B1D1
A1C1,B1D1![]() CC1,
CC1,![]() A1C1
A1C1 ![]() CC1=C1
CC1=C1
∴B1D1![]() 面A1C1CA,
--------------8’
面A1C1CA,
--------------8’
AE![]() 面A1C1CA
面A1C1CA
∴B1D1![]() AE
--------------10’
AE
--------------10’
(3)解法一:连结AC1,取AC1的中点为H,取AC的中点O,连接HO,
∵HO//EC且HO=EC
∴四边形HOCE为平行四边形,OC//HE即AC//HE ---------13’
连接BD1,易知四边形A1BCD1为平行四边形,则H为BD1和A1C的交点
∴HE![]() 平面B1DE
平面B1DE
AC![]() 平面B1DE
平面B1DE
AC//平面B1DE - ------------16’
解法二:延长BC与B1E延长线交于F,连DF
![]() E为棱CC1中点
E为棱CC1中点
∴![]() B1C1E
B1C1E![]()
![]() FCE
FCE
∴CF=C1B1=CB
∴CF//AD且CF=AD
∴ADFC为平行四边形
∴AC//DF --------------13’
![]() AC
AC![]() 平面B1DE
平面B1DE
DF![]() 平面B1DE
平面B1DE
∴AC//平面B1DE --------------16’
20.(本小题满分17分)
解:(1)由题意得:圆心为![]() 的中点
的中点![]() ,
,
![]() 圆C的方程为
圆C的方程为![]() --------------5’
--------------5’
(2)设射线所在直线方程为![]() ,将它代入
,将它代入![]() 得:
得:
![]() ,
,
![]() -------------7’
-------------7’
![]() 射线
射线![]() 与直线
与直线![]() 相交
相交![]() 与3同号
与3同号![]() ,
,
![]()
=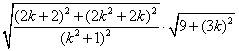
=![]() -------------9’
-------------9’
![]()
![]() 无最小值
-------------11’
无最小值
-------------11’
(3)![]()
![]() --------------13’
--------------13’
又![]()
![]() 代入上式得
--------------15’
代入上式得
--------------15’
![]() --------------17’
--------------17’