高一数学第一学期期末试卷
说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共22道题，其中第21题、第22题分“重点中学做”和“非重点中学做”.
试卷满分120分,考试时间120分钟.本次试卷不得使用计算器.
第Ⅰ卷（选择题 共40分）
一、选择题：（本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.）
1、设全集U＝{0,1,2,3,4},集合A={1，2，3,},B={2,3,4},则
=…………………（ ）
A、{0} B、{1} C、{0,1} D、{01,2,3,4}
2、已知角α满足sinα=
,tanα>0,则角α是 …………………………………………（
）
A、第一象限角 B、第二象限角 C、 第三象限角 D、第四象限角
3、若向量（cosα,sinα）与向量（3，4）垂直，则tanα＝……………………………………（ ）
A、 
B、
C、
D、
4、已知
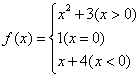，则
＝…………………………………………（ ）
A、－4 B、4 C、－3 D、3
5、已知tan28°=a,则sin2008°=………………………………………………………………（ ）
A、
B、
C、
D、
6、在边长为
的等边△ABC中，
=………………………（
）
A、－3 B、3 C、－1 D、1
| |
的部分图象如图所示，则
＝………………………（ ）
A、
B、1
C、－1
D、－
8、函数
的图象是……………………（ ）
y
y
y
y
 | |||||||
 | |||||||
 |  | ||||||
-1 O 1 x -1 O 1 x -1 O
1 x -1 O 1 x
A、 B、 C、 D、
9、已知
=1,
,
=0,点C满足：∠AOC＝30°，
且
，则
＝……………………………………………（ ）
A、
B、
C、
D、3
10、函数
的定义域为R，且存在零点，则实数a的取值范围是…………（ ）
A、[1,2] B、(1,2] C、[2,3) D、[2,3]
第Ⅱ卷（非选择题 共80分）
二、填空题：（本大题共7小题，每小题4分，共28分.把答案填在题中横线上.）
11、函数
的最小正周期是
.
12、函数
的定义域为 .
13、已知
=2,
=3,
=－1，那么向量与的夹角为＝
.
14、已知钝角α满足sinα=cos2α,则tanα= .
15、若函数
与
有相同的零点，则a=
.
16、1980年我国人均收入约为250美元，到2000年人民生活达到了小康水平，人均收入已超过800美元，若不低于此增长率递增，则到2020年，我国的人均收入至少有 美元.
17、给出下列命题：
①函数
是奇函数；②函数
的最大值为
；
③函数
在第一象限内是增函数；
④函数
的图象关于直线
成轴对称图形.
其中正确的命题序号是 .
三、解答题：（本大题共5小题，共52分.解答应写出文字说明、证明过程或演算步骤.）
18、（本小题满分10分）已知0<α<
<β<
,sinα=
,sinβ=
.
（1）求cosβ； （2）求tan(α+β).
19、（本小题满分10分）
.
（1）当
时,求
的值域；
（2）作出
在长度为一个周期的闭区间上的简图；
（3）说明的图象可由
的图象经过怎样的变化得到？
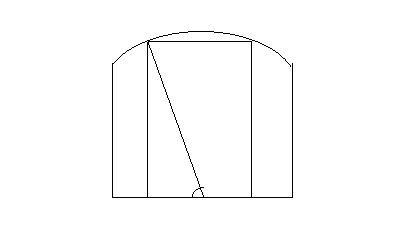
20、（本小题满分10分）如图，钢板材料ABCD，上沿为圆弧AD，其所在圆的圆心为BC中点O，AB、CD都垂直于BC，且AB=CD=米，BC=2米，现要用这块钢板材料截成一块矩形板EFGH（其中G,H在AD上，E,F在BC上），设∠BOH＝θ.
（1）求矩形EFGH的面积S关于θ的函数表达式S＝
；
（2）求矩形面积S的最大值.
21、（非重点中学做，本小题满分10分）
已知
(α为常数)，且函数的图象经过点（5，2）.
（1）求的解析式；（2）用单调性定义证明在定义域内为增函数.
21、（重点中学做，本小题满分10分）
已知向量＝
，
，
.
（1）当
时，求
及
的值；
（2）求
（
）的最大值.
22、（非重点中学做，本小题满分10分）
已知向量＝，，.
（1）当时，求及的值；
（2）求（）的最大值.
22、（重点中学做，本小题满分10分）
设二次函数
在区间[－2,2]上的最大值、最小值分别为M、m，集合A＝
.
（1）若A＝{1,2}，且
＝2，求M和m的值；
（2）若A＝{2}，且a≥1，记
，求
的最小值.
高一数学期末试卷答题卷
| 题号 | 一 | 二 | 三 | 总分 | 复分签名 | ||||
| 18 | 19 | 20 | 21 | 22 | |||||
| 得分 | |||||||||
|
一、选择题:（每小题4分，共40分）
|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1
|
二、填空题：(每小题7分，共28分）
11、 ；12、 ； 13、 ； 14、
15、 ；16、 ； 17、 ；
| 得分 | |
| 评卷人 |
三、解答题：（本大题共5小题，共52分.解答应写出文字说明、证明过程或演算步骤.）
18、解：
 | |||
 | |||
|
|
|
|
宁波市2007学年度第一学期高一数学期末试卷参考答案
一、选择题:（每小题4分，共40分）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | A | C | B | D | A | C | A | C | B |
二、填空题：(每小题４分，共28分）
11、 ； 12、(3,+∞)； 13、120°； 14、
；
15、1或－1； 16、2560； 17、①④.
三、解答题：（本大题共5小题，共52分.解答应写出文字说明、证明过程或演算步骤.）
18、解：（1）∵
，
又∵
∴ 
＝ 
（2）∵
,
, 
∴
∴
又∵
∴ 
=
=
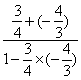10分
19、解：（1）=
=
∵ ∴
, 
∴所求值域为[－1,2]
（2）图略
（3）法1：可由的图象先向左平移
个单位，再将图象上各点的横坐标缩短到原来的
倍而得到。
法2：可由的图象先将图象上各点的横坐标缩短到原来的倍，再将图象向左平移
个单位而得到。
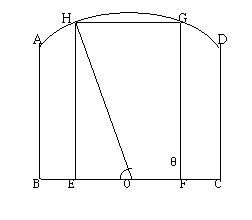
20、解：（1）在Rt△ABO中，由AB＝，BO＝1得：r＝AO＝2
在Rt△HEO中，由OH＝r=2, ∠BOH＝θ,得：HE＝2sinθ,EO＝2cosθ,
∴S＝＝EF×EH＝8 sinθ×cosθ＝4sin2θ.
（2）由（1）得S＝4sin2θ，∴θ=45°时，Smax＝4米2 .
21、（非重点中学做）解：（1）∵ ∴
，
又的图象过点（5，2）∴
，
＝
∴
（2）设
，
则
＝
＝
<0
∴
∴在定义域内为增函数.
21、（重点中学做）解：（1）∵＝，＝
∴
=
=
∴时，
，
又
＝
＝
∴时，＝
（2）∵, ∴0≤
≤1
∴＝
＝
令t＝（0≤t≤1）则
＝
∴ 当
>1即
时，此时t＝1，
当0≤≤1即0≤m≤2时，此时t＝，
当<0即m<0时，此时t＝0，
＝－1
∴
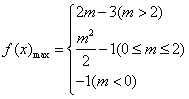
22、（非重点中学做）解：（1）∵＝，＝
∴==
∴时，，
又＝＝
∴时，＝
（2）∵, ∴0≤≤1
∴＝＝
令t＝（0≤t≤1）则＝
∴ 当>1即时，此时t＝1，
当0≤≤1即0≤m≤2时，此时t＝，
当<0即m<0时，此时t＝0，＝－1
∴
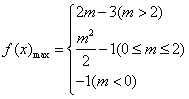
22、（重点中学做）解：（1）∵＝2， ∴c＝2
∵A＝{1,2}， ∴
有两根为1，2.
由韦达定理得，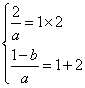
∴
∴
∵
， ∴ M＝
＝10，m＝
1
（2）∵A＝{2}， ∴
有相等的两根为2.
由韦达定理得，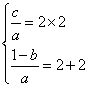
，
∴
＝
∵
， ∴对称轴为
＝
∵， ∴M＝＝10，m＝
＝
∴
∴