高一数学下册期中试卷
班级__________ 姓名__________ 学号__________ 分数
一、填空题（每小题4分，共40分）
1、写出终边在y轴上的角的集合：__________________。
2、已知角
的终边经过点
（
），则
的值为__________。
3、
的值为
。
4、已知
，则
__________。
5、The domain of the function 
is__________________。
6、函数
的最小正周期是_________________。
7、若
，化简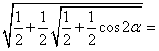
_____________。
8、函数
的单调增区间是__________。
9、直线
（
为常数）与正切函数
的图像相邻的两个交点间的距离为__________。
10、设
，由（1）+（2）可以得到下面的“三角式”：
，
按照上述的过程请将（1）和（2）通过代数变换类比得出一个结果为“0”的其他“三角式”： 。
二、选择题（每小题4分，共16分）
11、已知
，
，
，则m的取值为（ ）
（A）
或
（B）
（C）
或
（D）
12、已知
，则
的值为（
）
（A）0 （B）
（C）1 （D）
13、若
是周期为2的奇函数,则
可以是（ ）
（A）
（B）
（C）
（D）
14、在
中，
，
，
，则
等于（
）
（A）
（B）
（C）
（D）
三、解答题（第15、16、17题每小题8分，第18、19题每小题8分）
15、已知
，求值：
（1）
；
（2）
。
16、已知
，
（1）求
的值；
（2）若
，求
的值。
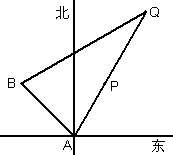17、如图，某船在A处望见北偏东30°有两个灯塔P、Q与它在同一直线上。当船向西北方向行驶10海里后，灯塔P恰在其正东方向上，灯塔Q在北偏东60°方向上，求灯塔P、Q之间的距离。
18、已知函数
；
（1）若
，求的最大值和最小值；
（2）当
的最大值为
时，求a，b的值；
（3）当
=1，且的最大值为K时，求K的取值范围。
19、是否存在锐角、
，使得（1）
，（2）
同时成立？若存在，求出和的值；若不存在，请说明理由。
答案
1、
2、
3、
4、2004
5、
6、
7、
8、
9、
10、
11、D 12、B 13、A 14、B
15、解：（1）原式
；
（2）原式
。
16、解：（1）∵
，
∴
①
①2得
，
∴
；
（2）∵
，
又∵
且，
∴
，
，
∴
，
∴
，
原式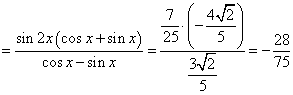
。
（2）另解：∵，∴
，
又∵，∴
，
，
原式
。
17、解：连结PB，由条件知
，
，
∴
，∴
，
在
中，由正弦定理得
，
∴
，
∴
。
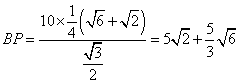答：灯塔P、Q之间的距离为
海里。
18、解：（1）若，则
；
；
（2）由题意得
……①
又的最大值为
，所以
，即
……②
由①②可知，
；
（3）
，即
，
因此
19、解：∵，∴
，
∴
，
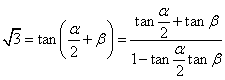又∵，
∴
，
∴
、
是一元二次方程
的两个实根，
∵
，∴
，
，
解得，
，
，
∵
，∴
，
又∵，∴
，
所以存在，满足条件。