高一数学下学期期末模拟考试
数学试卷2008.07.01
满分160分 考试用时 120分钟
一、填空题：（14×5）
1、函数
的单调递增区间是_______________.
2、若函数
的最小正周期是
，则
3、已知向量
与
的夹角为
，
_______________.
4、不等式
对
恒成立，则
的取值范围是______________.
5、
中，
，则
____________
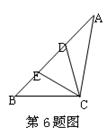
6、如图，在ΔABC中，D、E为边AB的两个三等分点，=，=2，试用
表示向量
= ____ .
7、设
为正实数，满足
，则
的最小值是_________________.
8、已知
，则
________________.
9、已知等比数列
中，
则
与
的等比中项为_______________.
10、已知线性约束条件是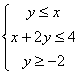
，则目标函数
的最大值为_____________.
11、已知数列
满足
，则
_______________.
12、下列命题中正确的序号是_____________.
①
是非零向量，若
∥
，∥
，则∥；
②若
，则
＝0；
③
是函数
的图象的一条对称轴；
④
的最大值为0.
13、形如
的符号叫二阶行列式，现规定=
，如果
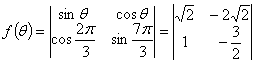
，则
=___________.
14、已知数列中，
，且是递增数列，求实数
的取值范围
.
二、解答题：
15、（本大题满分12分）已知函数
定义域为
，求实数的取值范围。
16、（本大题满分14分）在平面直角坐标系
中，以
轴为始边作两个锐角
，它们的终边分别与单位圆交于
两点。已知的横坐标分别为
.
（1）求
的值；
（2）求
的值.
17、（本大题满分14分）已知
,设函数
其中
（1）求
及其函数
的表达式.
（2）若函数的定义域为
时值域为
,求a,b的值.
18、（本大题满分16分）在等比数列中，
，公比
， 
， 且
是
与
的等比中项，
（1）求数列的通项公式；
（2）设
，数列
的前
项和为
，当
最大时，求的值.
19、（本大题满分16分）经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量
（千辆/小时）与汽车的平均速度
（千米/小时）之间的函数关系为
（1）在该时段内，当汽车的平均速度为多少时，车流量最大？最大车流量为多少？
（2）若要求在该时段内车流量超过10千辆/小时，则汽车的平均速度应在什么范围内？
20、（本大题满分18分）已知数列
的前项和为
，数列
满足：
，前项和为
，
设
（1）求数列的通项公式；
（2）求证：数列
是单调递减数列；
（3）若对
时，总有
成立，求自然数
的最小值
参考答案：
一、填空题
1、10 2、7
3、
4、
5、
6、
7、3
8、1
9、
10、12
11、
12、1，2，3 13、
14、
二、解答题
15、
.
16、（1）tan(
)；
（2）
.
17、（1）
；
（2）
或
.
18、（1）
；
（2）
.
19、（1）当
；
（2）汽车的平均速度在
的范围内时，>10.
20、(1)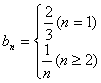
；
(2)证明
即可；
(3)自然数的最小值为3.