高一数学下学期期末考试卷2008.6
一、选择题( 每小题5分，共10题)
1．sin600°的值是
A． B． C．－ D ．－
2．右边的伪代码运行后的输出结果是
A．1，2，3 B．2，3，1 C．2，3，2 D．3，2，1
3．某城市有学校700所，其中大学20所，中学200所，小学480所．现用分层抽样的方法从中抽取一个容量为70的样本进行某项调查，则应抽取的中学数为
A．70 B．20 C．48 D．2
4．已知a，b都是单位向量，则下列结论正确的是
A． a·b=1 B．a 2= b 2 C．a // b D．a·b =0
5．cos80°cos35°+sin80°cos55°的值是
A． B．－ C． D．－
6．有一种彩票头奖的中奖概率是一千万分之一．若买五注不同号码，中奖概率是
A．千万分之一 B．千万分之五
C．千万分之十 D．千万分之二十
7．若向量a＝（1，1），b ＝（1，－1），c＝（－1，－2），则c =
A．－a－b B．－a+b C．a－b D．－a+b
8．下列说法正确的是
A．某厂一批产品的次品率为，则任意抽取其中10件产品一定会发现一件次品
B．气象部门预报明天下雨的概率是90﹪，说明明天该地区90﹪的地方要下雨，其余10﹪的地方不会下雨
C．某医院治疗一种疾病的治愈率为10%，那么前9个病人都没有治愈，第10个人就一定能治愈
D．掷一枚硬币，连续出现5次正面向上，第六次出现反面向上的概率与正面向上的概率仍然都为0.5．
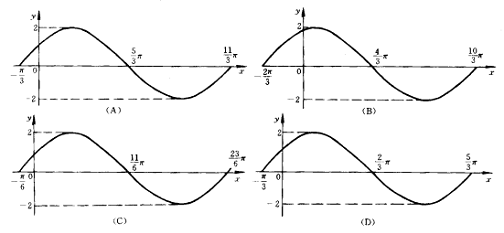9．函数y=2sin
在一个周期内的图象是
10．已知sin
，
是第二象限的角，且tan(
)= －
，则tan
的值为
A．－
B． C．－
D．
二、填空题（每小题5分，共6题）
11．若a =（－3，4），b =（5，12），则a·b = ．
12．函数y=sin2x－cos2x的最小正周期为 ．
13．右面伪代码运行后的输出结果S= ．
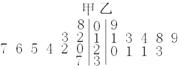14．某篮球学校的甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如右．则罚球命中率较高的是 ．
15．用不等号 “<”或“>”连结sin1___cos1．
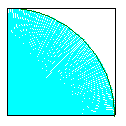
16．在正方形内有一扇形（见阴影部分），点P随意等可能落在正方形内，则这点落在扇形外且在正方形内的概率为 ．
三、解答题(共6题，其中17题10分，18－22每题12分)
17．已知
，
都是锐角，sin=
，cos=
，求sin(+)的值．
18．某热水瓶胆生产厂生产的10件产品中，有8件一级品，2件二级品，一级品和二级品在外观上没有区别．从这10件产品中任意抽检2件，计算：
（1）2件都是一级品的概率；
（2）至少有一件二级品的概率．
19．已知四边形ABCD为菱形，请用向量方法证明AC⊥BD．
 |
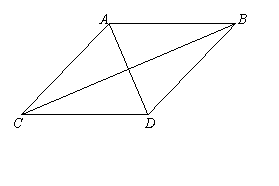20．修订后的《个人所得税法》规定：个人所得税的起征点为1600元，即收入不超过1600元，免于征税；超过1600元的按以下税率纳税：超过部分在500元以内（含500元），税率为5%，超过500元至2000元的部分，税率为10%.已知某厂工人的最高收入不高于3500元，试用流程图或者伪代码描述一个算法，对输入的个人收入，计算其所得税．
21．某花木公司为了调查某种树苗的生长情况，抽取了一个容量为100的样本，测得树苗的高度（cm）数据的分组及相应频数如下：
株；
株；
株；
株；
株；
株；
株；
株；
株．
（1）列出频率分布表；
（2）画出频率分布直方图；
（3）据上述图表，估计数据落在
范围内的可能性是百分之几？
22．函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等，请选择适当的探究顺序，研究函数f(x)=
+的性质，并在此基础上，作出其在
的草图．
参考答案与评分标准：
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | B | B | A | B | D | D | B | C |
二、填空题：
11．33； 12．
； 13． 55； 14．甲； 15． > ； 16． 1－．
三、解答题：
17．解：∵sin= ，且是锐角，∴cos=
．………………………2分
又∵cos= ，且是锐角，∴sin=
．……………………4分
∴sin(+)=sincos+cossin …………………………6分
=
． ………………………………10分
18．解：（1）设2件都是一级品为事件A．…………………………………1分
从10件产品中抽取2件，共有45个基本事件，且都是等可能的，…3分
而事件A的结果（即包含的基本事件数）有28种， …………………4分
则P（A）=
．
…………………………………………………6分
（2）设至少有一件二级品为事件B，………………………………………7分
则B是两个互斥事件：“抽取的2件产品中包含了一件一级品，一件二级品（记为B1）”与“抽取的2件产品均为二级品（B2）”的和． ………………8分
而P（B1）=
，P（B2）=
，
…………………9分
∴P（B）=P（B1+B2）= P（B1）+ P（B2） …………………10分
=
．
…………………………………………11分
答： 2件都是一级品的概率为；至少有一件二级品的概率为
．……12分
（2）另解 设至少有一件二级品为事件B，……………………………………7分
则
指抽出的2件中没有二级品，由（1）知A=． …………………9分
∴P（B）=1－P（）=1－P（A）
…………………10分
=1－=．…………………………………………………11分
答： 2件都是一级品的概率为，至少有一件二级品的概率为
．……12分
19．证明：∵ABCD为菱形，
∴
，且
． ……………………………2分
又
，
，……………………………………4分
∴
． …………………………………………………5分
∴
……………………………8分
…………………………………10分
=0． ……………………………………………11分
∴AC⊥BD ． ………………………………………………12分
20．解法一：（复合IF语句）
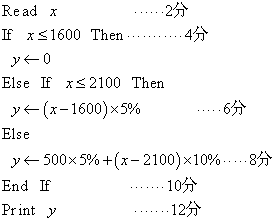
另解：（If语句嵌套）
另解：（行If语句）
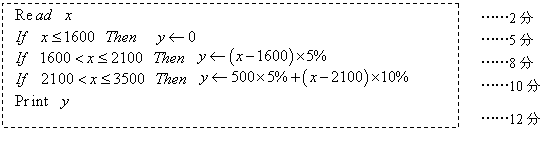
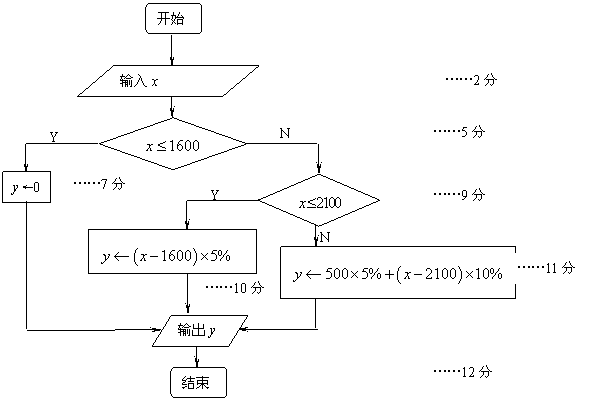
解法二
：流程图如下
 |
21．解
（1）画出频率分布表
| 分组 | 频数 | 频率 | 累积频率 |
| [107，109） | 3 | 0.03 | 0.03 |
| [109，111） | 9 | 0.09 | 0.12 |
| [111，113） | 13 | 0.13 | 0.25 |
| [113，115） | 16 | 0.16 | 0.41 |
| [115，117） | 26 | 0.26 | 0.67 |
| [117，119） | 20 | 0.20 | 0.87 |
| [119，121） | 7 | 0.07 | 0.94 |
| [121，123） | 4 | 0.04 | 0.98 |
| [123，125] | 2 | 0.02 | 1.00 |
| 合计 | 100 | 1.00 |
………………………….4分
（2）
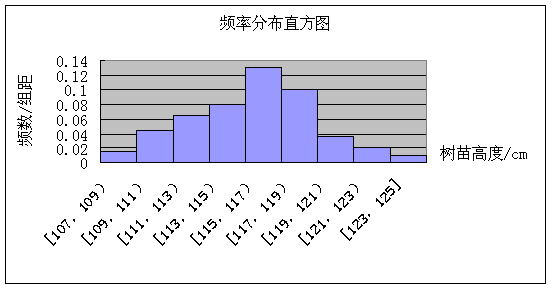
………………………8分
（3）由上述图表可知数据落在范围内的频率为：0.94－0.03=0.91，即数据落在范围内的可能性是91%．
…………………………12分
22．解：① ∵
∴
的定义域为
；…………………………2分
② ∵
，
∴
为偶函数；………………………………………………………4分
③ ∵
, ∴是周期为的周期函数；……………6分
④ 当
时，=
，
∴当时单调递减；当
时，
=
，
单调递增；又∵是周期为的偶函数，∴在
上单调递增，在
上单调递减（
）；……………8分
⑤ ∵当
时
；当
时
．∴的值域为
； ………………10分
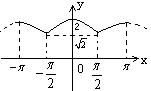
⑥由以上性质可得：在
上的图象如图所示：
…………………………………12分