高一数学下学期期末考试试卷（文理合卷）
命题人:王志勇 审题人:林春保
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1页至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟.
第I卷（选择题,共50分）
一、选择题：（本大题共10个小题；每小题5分，共50分。在每小题给出的四个选项中，只有一个选项是符合题目要求的。）
1. tan480
=（ ）
（A）．
（B）．
（C）．
（D）．
2．在△ABC中，已知
的值为（ ）
（A）．－2 （B）．2 （C）．±4 （D）．±2
3．如果
，那么 （ ）
（A）
（B）
（C）
（D）
在
上的投影相等
4．若向量
则
一定满足 （ ）
（A）的夹角等于
(B)
⊥
( C) 
∥
( D) ⊥
5.（理）在ΔABC中，已知
则ΔABC是（ ）
（A）．直角三角形 （B）． 等腰三角形
（C）．锐角三角形 （D）．等腰或直角三角形
（文）已知
，则
（ ）
（A）
（B） 
（C） 
（D）
6. 在
中，已知
是
边上一点，若
，则
（ ）
（A）．
（B）．
（C）．
（D）．
7．已知函数
，按向量平移所得图象的解析式为
，当为奇函数时，向量可以是（ ）
（A）
（B）
（C）
（D）
8. （理）已知函数y=sin
在
上是减函数,则
的取值范围是（ ）
（A）
（B）
（C）
（D）
（文）已知函数y=sin在上是增函数,则的值可以是（ ）
（A） 1 （B） 2 （C）-1 （D）-2
9．（理）已知
则函数
的最小值是 （ ）
（A）． 
（B）． 
（C）． 
（D）．
（文）关于x的方程4cosx-
恒有解,则m的范围为 ( )
（A）
（B）
（C）
（D）
10.已知向量
，并且满足关系：
，则的夹角的最大值为（ ）
（A）
（B）
（C）
（D）
鄂州市2007-2008学年度下学期期末考试
高 一 数 学（文理合卷）
第Ⅰ卷选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 得 分 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
第
卷 （非选择题 ，共100分）
二、填空题：(本大题共5小题，每小题5分，共25分. 把答案填在题中横线上.)
11.与向量
垂直的单位向量是
12. 平面上有三点A，B，C，满足
则
13. 不等式
的解集是
，则实数
14．已知
为互相垂直的单位向量，
，且
的夹角为锐角，则实数
的取值范围__________
15.下列命题正确的是 。
①在△ABC中，有A>B
②. 已知
=(2,3) , 
=(
,7) ,则在上的投影值为
③∥
存在唯一的实数
，使得
；
④函数y＝sinx在第一象限为增函数
⑤若
⑥设点P分有向线段
所成的比为
，则点P1分
所成的比为
三、解答题：（本大题共6小题，共75分，解答应写出必要的文字说明、证明过程及演算步骤。）
16
（本小题满分12分）解关于
的不等式：
.
17．（本小题满分12分）.
已知向量
，
，
．
（Ⅰ）求
的值；
（Ⅱ）若
，
，且
，求
的值．
18. (本小题满分12分) (本小题满分12分) 已知在△ABC中，a,b,c分别是角A,B,C的对边，又
,△ABC外接圆半径为
。
①求角C
②求△ABC面积的最大值
19. （本小题满分12分）某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计产量年递增10万只，第n次投入后，每只产品的固定成本为
（k＞0，k为常数，
且n≥0），若产品销售价保持不变，第n次投入后的年利润为
万元．
（1）求k的值，并求出的表达式；
（2）问从今年算起第几年利润最高?最高利润为多少万元?
20. (本小题满分13分) 设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
⑴若
用
；
⑵求证：AH⊥BC；
⑶设△ABC中，∠A＝60°，∠B＝45°，外接圆半径为R，用R表示．
21、（本小题满分14分）
（理科）已知
为锐角且tan
函数f（x）=x
,
数列｛a
｝的首项a
①求f（x）函数表达式 ②求证:
③求证：1<
…+
（文科）已知向量
,且
求
(1) 
及
;
(2) 若
的最小值是
,求实数的值
鄂州市2007-2008学年度下学期期末考试
高 一 数 学（文理合卷）
参考答案
一、选择题：（本大题共10个小题；每小题5分，共50分。）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | B | C | D | B | A | A | C | A | D | B |
二、填空题：（本大题共5小题，每小题5分，共25分。）
11、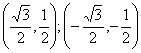
；
12、 
；
13、
；
14 、
； 15、①②.⑤；
三、解答题：（本大题共6小题，共75分。）
16、（本小题满分12分）
解：原不等式等式可化为
，……………………2分
当
时，原不等式的解集为
；……………………4分
当
时，原不等式可化为
且
，此时，则原不等式的解集为
；……………………7分
当
时，原不等式可化为
且，此时，则原不等式的解集为
；……………………11分
综上所述：当时，原不等式的解集为；
当时，原不等式的解集为；
当时，原不等式的解集为.……………………12分
17、（本小题满分12分）
解：
(1)因为
所以
又因为
，所以
，
即
；……………………6分
(2)
，
又因为
，所以 
，
所以
，所以
……………………12分
18、（本小题满分12分）
解：①由已知得
，
即
．……………………3分
，
．……………………5分
②
，面积S有最大值
．……………………12分
19、（本小题满分12分）
解：（1）由，当n＝0时，由题意，可得k＝8，
……………………3分
所以
． ……………………6分
（2）由
．
当且仅当
，即n＝8时取等号，
所以第8年工厂的利润最高，最高为520万元. ……………………12分
20、（本小题满分13分）
解：⑴
……………………3分
⑵
∴O为△ABC的外心．……………………5分
即
……………………8分
⑶在△ABC中，∠A＝60°，∠B＝45°，O为△ABC的外心，则∠BOC＝2∠A＝120°，
∠AOC＝2∠B＝90°，∴∠AOB＝150°。……………………10分
＝
……………………13分
21、（本小题满分14分）
解（理科）：①由tan
得
,又为锐角
f(x)=
……………………3分
②
=
,
又
不恒等于0，故
……………………6分
③设
…+
g（n）-g（n-1）=
>0
故g（n）的最小值为g（2）=
=
所以g（n）
……………………9分
…+
…+
，显然，
故 …+
成立。……………………14分
（文科）解：⑴
……………………2分
……………………5分
⑵
① 当
时，当县仅当
时，
取得最小值－1，这与已知矛盾；
……………………8分
②当
时，取得最小值
，由已知得
；
……………………11分
③当
时，取得最小值
，由已知得
解得
，这与
相矛盾，综上所述，为所求.
……………………14分