高一数学下学期期末试卷
（考试时间90分钟，满分100分）
一、填空题（共10小题，每小题3分，共30分）
1、若角
的终边上有一点
，则
的值是___________________.
2、计算：
____________.
3、化简：
_____________.
4、计算：
_____________.
5、函数
的定义域是______________________.
6、函数
(
)的单调递增区间是_____________________.
7、已知
，
，则
的值为___________________.
8、方程：
的解集是_______________________________________.
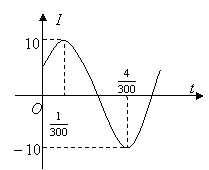
9、电流强度
（安）随时间
（秒）变化的函数
（
，
）的图象如图所示，则当
秒时，电流强度是
安.
10、已知函数
，给出下列四个命题：
（1）若
则
；
（2）直线
是函数图像的一条对称轴；
（3）在区间
上函数是减函数；
（4）函数的图像可由
的图像向右平移
个单位而得到.其中正确命题的序号是___________________.
二、选择题（共6小题，每小题3分，共18分）
11、化简：
得
（
）.
A.
B. 
C. 
D. 
12、在
中，若
则此三角形一定是 （ ）
A．钝角三角形 B．直角三角形 C．锐角三角形 D．形状不确定
13、已知：
，则
等于
（ ）
A.
B.
C.
D.
14、5、在△ABC中,C= 2B, 则
等于
(
)
A、
B、
C、
D、
15、函数
的反函数
则的定义域为（ ）
A.
B.
C.
D.
16、若
，则函数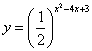
的值域为 （ ）
A、
B、
C、
D、
三、解答题（共5小题，共计52分，每小题要有必要的解题过程）
17、（满分10分）（1）解方程： 
；
（2）已知：
，解方程：
.
18、（满分10分）锐角中，
分别是角
的对边长，
，
（1）求：边长
；（2）求：中最小内角的正弦值和最大内角的余弦值.
19、（满分10分）已知函数
（1）求：函数的最大值及取得最大值时的值；
（2）在给出的直角坐标系中，用五点作图法画出函数
一个周期内的图像
| x | |||||
| y |
.
20、（满分12分）已知
(1)求的定义域;
(2)证明的图象关于原点对称
(3)求使
的取值范围.
21、（满分10分）设函数
（
），给出以下四个论断：①它的图像关于直线
对称；②它的图像关于点（
）对称；③它的最小正周期是
；④它在区间
上是增函数.以其中的两个论断作为条件，余下的两个论断作为结论，写出你认为正确的两个命题，并对其中的一个命题加以证明
参考答案：
一、填空题
1、
2、1
3、
4、
5、
6、
7、
8、
9、5 10、2,3
二、选择题
11、D 12、 A 13、 B 14、A 15、 D 16、C
三、解答题
17、解：（1）
即
解得：
经检验：
是原方程的根.
（2）由已知
①当
时，可化为：
或
②当
时可化为：
或
综上：原方程的解集为
18、解：（1）
（2）由余弦定理得：
为最小角，
为最大角
，
=
19、解：（1）
当
， 即
时，
函数的最大值为
.
（2）略.
20、解：（1）
，
，所以f(x)的定义域为：
证明：（2）由（1）f(x)的定义域为：可知定义域关于原点对称.
，即
，所以，函数f(x)是奇函数，因此，f(x)的图象关于原点对称
解：（3）f(x)>0 即，
① 当
时， 得，
解得，
.
②当
时 得，
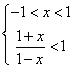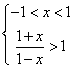解得，
.
21、解：两个正确的命题为 1）①③
②④；2）②③①④.
命题1）的证明如下：由题设和③得
=2，
.
再由①得 
（
）， 即
（），
因为，得
（此时
），所以
.
当
时，
，
，即，经过点（）
所以，它的图像关于点（）对称； 由， 
， 
的单调递增区间是
当
时， 为
，而区间是的子集
所以，它在区间上是增函数
(同理可证2)成立.)