高一数学数列单元考试题样稿（2008.03.22）
一、选择题
1、在等差数列
中，
=9，
=3，则
= B
A、－3 B、0 C、3 D、6
2、在等差数列
中，
那么
（ ）.B
A．－9 B．－8 C．－7 D．－4
3、等比数列｛
中 
，
，则
C
A． 33 B． 72 C． 84 D． 189
4、在等比数列{an}中，a9+a10=a(a
),a19+a20=b,则a99+a100的值为（ ）A
A．
B．（
）9 C．
D．（）10
5、在数列{an}中，a1=2,an+1=2an+2,则a100的值为（ ）B
A．2100-2 B．2101-2 C．2101 D．215
6、已知数列{
}的前
项和
，第
项满足
，则
（ ）B
A．9 B．8 C．7 D．6
7、设数列{an}是首项为50，公差为2的等差数列；{bn}是首项为10，公差为4的等差数列，以ak、bk为相邻两边的矩形内最大圆面积记为Sk，若k≤21，那么Sk等于 （ ）
A．（2k+1）2π B．（2k+3）2π C．（2k+12）2π D．（k+24）2π
8、我们把1，3，6，10，15，……这些数叫做三角形数，因为这些数目的点子可以排成一个正三角形（如下图）
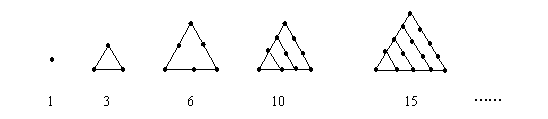
则第七个三角形数是( ) B
A、27 B、28 C、29 D、30
二、填空题
9、若三个数
成等比数列,则 
答: 
10、在等差数列
中，
表示前n项和，
，则
答:54
11、在数列
中
，且
，则
．
12、定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。已知数列
是等和数列，且
，公和为5，那么
的值为______________，这个数列的前n项和
的计算公式为________________
当n为偶数时，
；当n为奇数时，
三、解答题
13.(本题满分8分)设等差数列
的前项和为
，且
，
.
求数列的通项公式.
解：（1）设数列首项为a1，公差为d，则
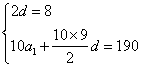------------------------------------------------------3分
解得a1=1，d=4 ------------------------------------------------------6分
∴=4n-3
------------------------------------8分
14. .(本题满分8分) 已知数列的前n项和为Sn，且
求数列的通项公式.
解: 
故数列是以3为首项,
为公式的等比数列,故
3
15.
.(本题满分8分)已知等比数列，是其前项的和，且
.
（1）求数列的通项公式；
（2）设
，求数列
的前项和
；
解（1）设数列的公比为
，则
∴
则
（2）由（1）可知
所以数列
是一个以
为首项，1为公差的等差数列
∴
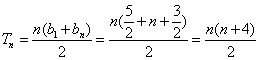
16. .(本题满分8分) 甲、乙两物体分别从相距70 m的两处同时相向运动，甲第一分钟走2 m，以后每分钟比前1分钟多走1 m,乙每分钟走5 m.
(1)甲、乙开始运动后，几分钟后第1次相遇?
（2）如果甲、乙到达对方起点后立即折返，甲继续每分钟比前1分钟多走1 m，乙继续每分钟走5 m，那么开始运动几分钟后第二次相遇？
1）设n分钟后第1次相遇，依题意得2n＋＋5n＝70
整理得：n2＋13n－140＝0，解得：n＝7，n＝－20(舍去）(3分)
（2）设n分钟后第2次相遇，依题意有：2n＋＋5n＝3×70
整理得：n2＋13n－6×70＝0，解得：n＝15或n＝－28(舍去）(7分)
答: 第1次相遇在开始运动后7分钟, 第2次相遇在开始运动后15分钟.……(8分)
17. .(本题满分8分)已知等差数列的首项为
，公差为
，且不等式
的解集为
.
（1）求数列的通项公式及前n项和公式 ；
（2）若数列满足
，求数列的前n项和.
解 ：（1）∵
的解集为，根据不等式解集的意义
可知：方程
的两根为
、
．
利用韦达定理不难得出
．
由此知
，
………………………………………4分
（2）由（1）可得：
①
②
由② - ①得：
…………………………………………………...8分
18. (本题满分10分)
已知数列
（I）若a1=2，证明
是等比数列；
（II）在（I）的条件下，求的通项公式；
（III）若
且
证明数列{
}的前n项和Sn满足Sn<1.
解（I）
，
由已知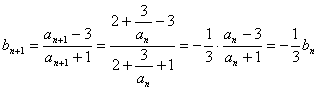
，
是首项为
，公比为的等比数列.…………………………3分
（II）由（I）知
，
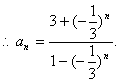……………………………………………………6分
（III）
，
，
=
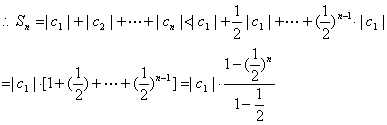
，………………………………………………………7分
，
即
，
…………………………………………10分
19. .(本题满分10分)
函数
是定义在R上的偶函数，且
，当
时，
R)，记函数
的图象在
处的切线为l，
．
(1)求在[0，1]上的解析式；
(2)求切线l的方程；
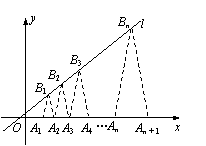
(3)点列B1(b1，2)，B2(b2，3)，…，Bn(bn，n + 1)在l上，A1(x1，0)，A2(x2，0)，…，An(xn，0)依次为x轴上的点，如图，当
N*，点An、Bn、An + 1构成以
为底边的等腰三角形，若
，且数列
是等差数列，求a的值和数列的通项公式．
(1)解：
，
是周期为2的周期函数. 2分
当0≤x≤1时，－2≤－2 + x≤－1，
，
整理得
. 4分
，由于
.
． 6分
(2)解：由题意切点为即
，l的斜率为
，
由直线点斜式方程知l的方程为
8分
(3)解：
点
在直线上，
.
又
为等腰三角形，
，即
由此有：
.两式相减得：
.
数列的所有奇数项、所有偶数项分别构成以2为公差的等差数列 10分
又
.
，
.
. 12分
当且仅当
，即
时，为等差数列.
此时数列的通项公式为
14分