数列复习题(1)答案
年级__________班次 ___ 学号 ____ 姓名___________________
一、 基础过关
(一) 选择题
1. 若数列 {an}的通项公式是an=,则数列 {an} 是( B )
A.递减数列 B.递增数列
C.摆动数殓 D.常数列
2. 数列{-n2+11n-30}的最大项是( C )
A.第5项 B.第6项
C.第5项和第6项 D.第4项和第5项.
3. 在等差数列{an}中,d=2,an=11,Sn=35,则a1为( D )
A.5或7 B.3或5
C.7或-1 D.3或-1.
4. 某工厂去年产值为a,计划在5年内每年比上一年产值增长10%,从今年起五年内这个工厂的总产值( D )
A.1.14a B. 1.15a
C.11(1.16-1)a D.11(1.15-1)a.
5. 制造某种产品,计划经过两年后要使成本降低36%,则平均每年应降低成本( D )
A.6% B.9% C.18% D.20%
(二) 填空题
6. 已知数列{an},a1=1,an=1+ (n∈N,n≥2),则a5=_________.
7. 已知数列{an}的通项公式为an=cn+,且a2=,a4=,则a10=______.
8. 写出下列数列的一个通项公式:
(1) 3,8,15,24,35,……;
(2) ,-,,-,,…….
(1) an=n(n+2) ;
(2) an=(-1)n+1.
9. 已知等比数列(an)中,a3=1,a8=32,则a12=___512___.
10. 某种产品平均每三年降低价格的,目前售价为270元,9年前此产品的价格为__640__.
11. 1·2+2·4+3·8+…+10·210=__18434_.
12. 已知数列{an}中,an=2n+2n-1,则前n项和Sn=__n2+2n+1-2__.
二、 技能提升
(一) 选择题
13. 三个从小到大的数构成公差为的等差数列,且它们的和等于它们的积,则此三个数是( D )
A.3-,3,3+
B.3-,3,3+或-3-,-3,-3+
C.-,0,;
D.-,0,或3-,3,3+或-3-,-3,-3+
14.
已知数列{an}是公比为q (q≠1)的等比数列,则数列①![]() ;②
;②![]() ;③
;③![]() ;④{anan+1}:⑤ {an+an+1}中,等比数列的个数为( B
).
;④{anan+1}:⑤ {an+an+1}中,等比数列的个数为( B
).
A.2 B.3 C.4 D.5
提示:②、③、④是等比数列,当q=-1时,⑤不是等比数列.
15. 若某等比数列中,前7项的和为48,前14项的和为60,前21项的和为( D )
A.180 B.108 C.75 D.63
16. 某工厂预计今年十二月份产量是今年一月份产量的m倍,则该厂今年的月平均增长率是( B )
A.+1 B. -1
C.-1 D. -1.
(二) 填空题
17. 数列{an}中,a1a2a3…an=n2 (n∈N+),则a2005=_______.
18. 所在被3整除的两位数的个数是_30___,这些数的和是__1665___
19. 已知数列{an},a1=-1,an+1=an+n (n∈N+),则数列的通项公式是an=___
20. 在等差数列{an}中,a1=3,a100=36,则a42+a59=____39_____.
21. 已知等比数列(an)中,a3=1,a8=32,则a12=___512___.
22. 在等差数列{an}中,a4+a6+a8+a10+a12=120,则2a9-a10=___24___.
提示:2a9=a8+a10
23. 在2与7之间插入n个数,使得包括2和7在内的n+2个数组成以2为首的等差数列,如果这个等差数列的前16项的和为56,则n=_24_.
24. 在等差数列{an}中,a1+a2+…+a50=200,a51+a52+…+a100=2700,则d=__1_,a1=_-20.5_
25. 若等差数列共有2n+1(n∈N+)项,且奇数项的和为44,偶数项的和为33,则项数=__7___.
提示:==,∴ n=3
26. 正项等比数列{an}中,a6a15+a9a12=30,则log15(a1a2a3…a20)=__10____.
提示:由a6a15=a9a12,得a9a12=15
∴ a1a2a3…a20=(a9a12)2=1510
27. 如果将20,50,100各加上同一个数能组成一个等比数列,那么这个数列的公比为_____.
28. 已知-1,a1,a2,-4成等差数列,-1,b1,b2,b3,-4成等比数列,则=____.
(三) 解答题
29. 求由通项公式an=-2n2+11n+8所给定的数列{an}的最大项
解法1:an=-2n2+11n+8
=-2(n-)2+8+
∵ n∈N+ ∴ n=3时,an取最大值为23
即数列中的最大项是an=23.
解法2:设数列中的最大项是an,则
![]()
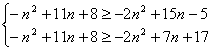
∴ ≤n≤
又∵ n∈N+ ∴ n=3
∴ 最大的项为a3=23.
30. 已知等差数列{an}满足a3·a7=-12,a4+a6=-4,求数列{an}的通项公式.
解法1:设公差为 d,首项为a1,由题设可知,
(a1+2d)(a1+6d)=-12 ①
(a1+3d)+(a1+5d)=-4 ②
联立解①②得:![]() 或
或![]()
an=2n-12或an=-2n+8.
解法2:∵{an}是等差数列,
∴ a3+a7=a4+a6=-4
又∵ a3·a7=-12
∴ a3和a7是方程x2+4x-12=0的两个根
解方程,得:x1=2,x2=-6
①当a3=2,a7=-6时,得a1=6,d=-2
∴ an=8-2n
②当a3=-6,a7=2时,得a1=-10,d=2
∴ an=2n-12.
31. 设{an.}为等差数列,Sn为等数列{an.}的前n项和,已知S7=7,S15=75,设Tn=为数列![]() 的前n项和,求Tn.
的前n项和,求Tn.
解:由已知知S7≠S15,∴ 数列{an.}的公差不为零,于是可知Sn是n的常数项为零的二次式,设Sn=An2+Bn (A≠0),则
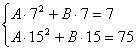
解之,得A=,B=-
∴ Sn=n2-n ∴ =n-,
∴![]() 是以-2为首项,为公差的等差数列.
是以-2为首项,为公差的等差数列.
∴ Tn=n·(-2)+·=n2-n.
32. 在等差数列{an}中,已知a1=25,S9=S17,问数列前多少项的和最大,并求出最大值.
解法1:由题意知17a1+·d=9a1+·d
∵ a1=25,∴ d=-2
∴ Sn=25n+×(-2)=-n2+26n
=-(n-13)2+169
∴ 当n=13时,Sn取最大值为169.
解法2:同解法1,求出d=-2,
由an≥0,得n≤13.5,
故当n≤13时an>0,当n≥14时,an<0
∴ n=13时,Sn取最大值为169.
33. 已知数列{an}为等比数列
(1) 若a5=4,a7=16,求a12;
(2) 若a4-a2=24,a2+a3=6,an=125,求n.
解:(1)由题意,得q2===4 ∴ q=±2
当q=2时,a12=a7·q5=8·25=256
当q=-2时,a12=a7·q5=8·(-2)5=-256.
(2) 由题意,得:
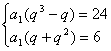 解之,得
解之,得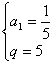
∴ an=()·5n-1=5n-2=125
解之,得:n=5.
34. 若数列(an)的前n项和Sn=2an+1,证明数列{an}成等比数列,并求出an.
证明:当n=1时,Sn=2a1+1=2×(-1)+1=-1
当n≥2时,an=Sn-Sn-1=2an+1-(2an-1+1)
=2an-2an-1
∴ an=2an-1 (n≥2)
∴=2
∴ {an}是以-1为首项,以2为公比的等比数列
∴ an=(-1)·2n-1.
35. 已知四个正数成等比数列,其积为16,中间两数之和为5,求这四个数及公比.
解:设这四个正数为:a,aq,aq2,aq3,由题设知它们的积a4q6=16,即aq·aq2=4>0.
又aq+aq2=5,
∴ aq,aq2是方程x2-5x+4=0的两实根
∴ x=1或x=4,即![]() 或
或![]()
∴ ![]() 或
或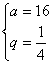
∴ 所求四个数为:,1,4,16或16,4,1,.
36. 已知等比数列{an}各项均为正数,Sn=80,S2n=6560,且在前n项中最大项为54,求n.
解:∵ Sn=80,S2n=6560, ∴ q≠1,q>0.
∴ 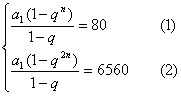
(2)÷(1),得1+qn=82 ∴ qn=81
又q>0,∴ q>1
∴ a1,a2,a3,…,an中,an最大.
∴ an=54=a1qn-1 ∴ ·qn=54
== (3)
又将qn=81代入(1)得=1 (4)
联立解(3)、(4)得a1=2,q=3,n=4.
37. 某城市2003年底人口为500万,人均居住面积为20平方米,如果该城市每年人口平均增长率为1%,每年平均新住房面积100万平方米,到2008年底,该市人均住房面积是多少(精确到0.01平方米)
解:设2003年底住房面积总数为a1,相应地2008年底住房面积总数为a6,则a1,a2,…,a6成等差数列,且a1=20×500万平方米,从而a6=a1+5d=10500万平方米.
另外,2003年底人口为b1,相应地,2008年底人口为b6,则b1,b1,…,b6成等比数列,且b1=300万平方米,从而b6=b1·q5=500·1.015.
故,2008年底人均住房面积为
=≈=19.98平方米.
38. (1)从1月起,若每月初存入100元,月利率是1.65‰并按单利计算,到第12月底本息和是多少?
(2)若一年定期的年利率为p,三年期年利率为q(均按单利计算),如果存一年定期的,一年后取出本息,再一起存入一年定期,这样三年后所取出的本息与直接存三年定期比较,还是直接存三年期的合算,请问p,q应怎样的关系?
解:(1)第一个月存入银行100元,到期利息应为100×12×1.65‰,到期利息应为100×11×1.65‰,….
∴ 共得本息和为100×12+100×(12+11+…+2+1)×1.65‰=1212.87元.
(2)设本金为A元,则直接存三年定期,到期本息和为A(1+3q);而一年后取出再转存的,三年后本息和应为A(1+p)3.
由题意应有:A(1+3q)>A(1+p)3.
解之,得:q>.
三、 智力挑战
39. 已知函数f(x)=,且数列{an}满足a1=2,an+1=f-1(an),求an.
解:∵ f(x)= ∴ f-1(x)=
∴ an+1= ∴ a3n+1=a3n+2
∴ a3n+1-a3n=2
∴ 数列{a3n}是等差数列,首项为8,公差为2.
∴ a3n=8+(n-1)×2=2n+6
∴ an=
40. 已知数列{an}中相邻两项an,an+1是关于x的方程x2+3nx+cn+n2=0 (n∈N+)的两实根,且a1=1,求c1+c2+c3+…+c2006的值.
解:由题意,得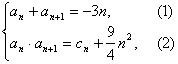
由(1)知an+1+an+2=-3(n+1), (3)
(3)-(1)得:an+2-an=-3
∴ 数列a1,a3,a5,…,a2n-1,…与数列a2,a4,a6,…,a2n,…都是公差为-3的等差数列,
∴ a2n-1=a1+(n-1)·(-3)=4-3n,
a2n=a2+(n-1)·(-3)=-1-3n.
由(2)得:c2n-1=a2n-1·a2n-·(2n-1)2=-.
c2n=a2n·a2n+1-·(2n)2=-1.
∴ c1+c2+…+c2006=1003×(-1-)=-