高一数学---3.1直线的倾斜角与斜率
两条直线平行与垂直的判定
[要点分析]
一、直线的倾斜角与斜率
1、倾斜角的概念：（1）倾斜角：当直线
与x轴相交时，取x轴作为基准，x轴正向与直线向上方向之间所成的角a叫做直线的倾斜角。
（2）倾斜角的范围：当与x轴平行或重合时，规定它的倾斜角a为0°因此0°≤a＜180°。
2、直线的斜率
（1）斜率公式：K=tana（a≠90°）
（2）斜率坐标公式：K=
（x1≠x2）
（3）斜率与倾斜角的关系：一条直线必有一个确定的倾斜角，但不一定有斜率。当a=0°时，k=0；当0°＜a＜90°时，k＞0，且a越大，k越大；当a=90°时，k不存在；当90°＜a＜180°时，k＜0，且a越大，k越大。
二、两直线平行与垂直的判定
1、两直线平行的判定：
（1）两条不重合的直线的倾斜角都是90°，即斜率不存在，则这两直线平行；
（2）两条不重合的直线，若都有斜率，则k1=k2 Û 
∥
2、两直线垂直的判定：
（1）一条直线的斜率为0，另一条直线的斜率不存在，则这两直线垂直；
（2）如果两条直线、的斜率都存在，且都不为0，则⊥ Û k1·k2=－1
[例题分析]
例1、△ABC为正三角形，顶点A在x轴上，A在边BC的右侧，∠BAC的平分线在x轴上，
求边AB与AC所在直线的斜率。
例2、若经过点P（1－a，1＋a）和Q（3，2a）的直线的倾斜角为钝角，求实数a的取值范围。
例3、已知经过点A（－2，0）和点B（1，3a）的直线与经过点P（0，－1）和点Q（a，－2a）的直线互相垂直，求实数a的值。
[课后练习]
1、若经过P（－2，m）和Q（m，4）的直线的斜率为1，则m=（ ）
A、1 B、4 C、1或3 D、1或4
2、若A（3，－2），B（－9，4），C（x，0）三点共线，则x=（ ）
A、1 B、－1 C、0 D、7
3、直线经过原点和（－1，1），则它的倾斜角为（ ）
A、45° B、135° C、45°或135° D、－45°
4、下列说法正确的有（ ）
①若两直线斜率相等，则两直线平行；
②若∥，则k1=k2；
③若两直线中有一条直线的斜率不存在，另一条直线的斜率存在，则两直线相交；
④若两直线斜率都不存在，则两直线平行。
A、1个 B、2个 C、3个 D、4个
5、直线、的斜率是方程x2－3x－1=0的两根，则与的位置关系是（ ）
A、平行 B、重合 C、相交但不垂直 D、垂直
6、给定三点A（1，0）、B（－1，0）、C（1，2），则过A点且与直线BC垂直的直线经过点（ ）
A、（0，1） B、（0，0） C、（－1，0） D、（0，－1）
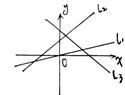7、如右图中直线、、
的斜率分别为k1、k2、k3。则
A、k1＜k2＜k3 B、k3＜k1＜k2
C、k3＜k2＜k1 D、k1＜k3＜k2
8、已知点M（2，2）和N（5，－2），点P在x轴上，且∠MPN为直角，求点P的坐标。
9、求证：A（1，－1），B（―2，―7），C（0，－3）三点共线。
10、已知A（1，－1），B（2，2），C（3，0）三点，求点D，使直线CD⊥AB，且CB∥AD。
参考答案
[例题分析]
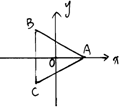
例1、如右图，由题意知∠BAO=∠OAC=30°
∴直线AB的倾斜角为180°－30°=150°，直线AC的倾斜角为30°，
∴kAB=tan150°=－
kAC=tan30°=
例2、∵k=
且直线的倾斜角为钝角，
∴＜0 解得－2＜a＜1
例3、的斜率k1=
当a≠0时，的斜率k2=
∵⊥ ∴k1·k2=－1，即a×
=－1 得a=1
当a=0时，P（0，－1），Q（0，0），这时直线为y轴，A（－2，0）、B（1，0），这时直线为x轴，显然⊥
综上可知，实数a的值为1和0。
[课后练习]=
1、A 2、B 3、B 4、A 5、D 6、A 7、B
8、设点P的坐标为（x，0）
kPM=
， kPN=
∵∠MPN为直角 ∴PM⊥PN，kPM·kPN=－1
∴×=－1
解得x=1或x=6
∴点P的坐标为（1，0）或（6，0）
9、∵kAB=2 kAC=2 ∴kAB= kAC
∴直线AB与AC的倾斜角相同且过同一点A
∴直线AB与AC为同一直线，故A、B、C三点共线。
10、设D（x，y），则kCD=
，kAB=3，kCD=－2，kAD=
∵kCD ·kAB=－1， kCB= kAD
×3=－1 x=0
∴ ∴ 即D（0，1）
－2=
y=1