高一数学算法与统计训练题 2008-3-11
一选择题
1.下列说法错误的是（ ）
A.不管是简单随机抽样还是系统抽样、分层抽样都要保持每个个体被抽是等可能的
B.样本的数字特征是随机的,这种随机性由样本的随机性引起
C.总体的数字特征是一定的,不存在随机性
D.当知道样本的频率分布直方图和平均数、标准差时,可以准确的知道总体的精确分布情况
2.把二进制数110011(2)化为非二进制数，下列结果正确的是( )
A. 51 B. 203(5) C. 125(6) D. 46(8)
3.甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表
| 甲的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 5 | 5 | 5 | 5 |
| 乙的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 6 | 4 | 4 | 6 |
| 丙的成绩 | ||||
| 环数 | 7 | 8 | 9 | 10 |
| 频数 | 4 | 6 | 6 | 4 |
分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
4.工人月工资（元）依劳动生产率（千元）变化的回归直线方程为
，下列判断正确的是
（ ）
A.劳动生产率为1000元时，工资为50元 B.劳动生产率提高1000元时，工资提高150元
C.劳动生产率提高1000元时，工资约提高90元 D.劳动生产率为1000元时，工资为90元
5.为研究变量
和
的线性相关性，甲、乙二人分别作了研究，利用线性回归方法得到回归直线方程
和
，两人计算知
相同，
也相同，下列正确的是
( )
A.与重合 B.与一定平行 C.与都过点
D. 和一定相交
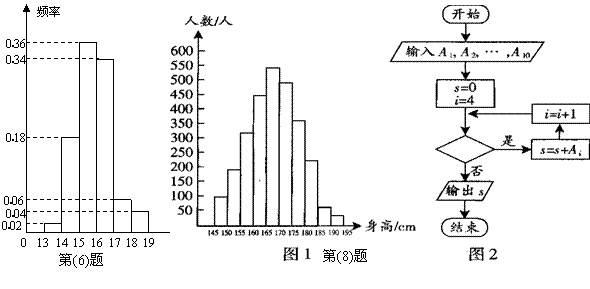6.某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；……第六组，成绩大于等于18秒且小于等于19秒
右图是按上述分组方法得到的频率分布直方图，设成绩小于17秒的学生人数占全班人数的百分比为，成绩大于等于15秒且小于17秒的学生人数为，则从频率分布直方图中可以分析出和分别为
( )
A 
B 
C 
D 
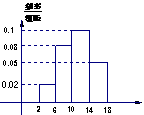7.如图为某样本数据的频率分布直方图,则下列说法不正确的是( )
A.[6,10)的频率为0.32
B.若样本容量为100,则[10,14)的频数为40
C. 若样本容量为100,则
的频数为40
D.由频率分布布直方图可得出结论:估计总体大约有10%分布在[10,14)
8.图l是某县参加2007年高考的学生身高条形统计图，从左到右的各条形表示的学生人数次记为
(如
表示身高(单位：cm)在[150,155)内的学生人数)．图2是统计图l中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～180cm(含160cm，不含180cm)的学生人数，那么在流程图中的判断框内应填写的条件是( )
A．i < 9 B．i < 8 C．i < 7 D． i < 6
二填空题
9. 某校1000名学生中，O型血有400人，A型血有250人，B型血有250人，AB型血有100人，为了研究血型与性格的关系，按照分层抽样的方法从中抽取样本. 如果从A型血中抽取了10人，则从AB型血中应当抽取的人数为 .
10. 假设要考察某公司生产的500克袋装牛奶的质量是否达标，现从800袋牛奶中抽取60袋进行检验，利用随机数表抽取样本时，先将800袋牛奶按000，001，…，799进行编号，如果从随机数表第8行第7列的数开始向右读，请你衣次写出最先检测的5袋牛奶的编号 ___ （下面摘取了随机数表第7行至第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
11.在抽取调查产品的尺寸过程中，将其尺寸分成若干组，
是其中一组，抽查出的个体在该组上的频率为m ，该组上的直方图的高为h，则
____________.
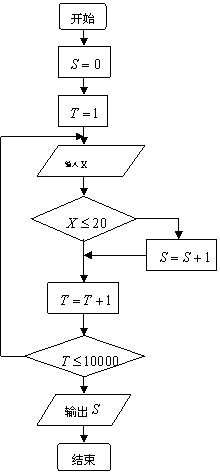12.下列程序执行后输出的结果是___________
|
13.为调查深圳市中学生平均每人每天参加体育锻
炼时间
（单位：分钟），按锻炼时间分下列四种
情况统计：①0～10分钟；②11～20分钟；
③21～30分钟；④30分钟以上．有10000名中学
生参加了此项活动，下图是此次调查中某一项的流
程图，其输出的结果是6200，则平均每天参加体育
锻炼时间在0～20分钟内的学生的频率是_________
三解答题
14. 10辆汽车在同一条件下进行耗油1L所行路程实验,得到如下样本数据（单位:km）:13.7,12.7,14.4,13.8,13.3,12.5,13.5,13.6,13.1,13.4，其分组如下:
| 分组 | 频数 | 频率 |
| [12.45,12.95） | ||
| [12.95,13.45） | ||
| [13.45,13.95） | ||
| [13.95,14.45） | ||
| 合计 | 10 | 1.0 |
（1）完成上面频率分布表；
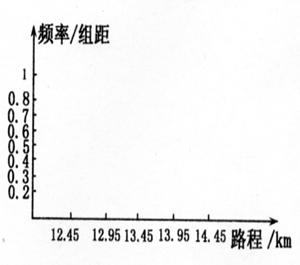
（2）根据上表,在给定坐标系中画出频率分布折线图,并根据样本估计总体数据落在[12.95,13.95）中的比率；
（3）根据上图求1L油所行距离在[12.95,14.45]内的车辆数.
(4)根据频率分布直方图,估计样本数据的众数、中位数、平均数.
15. 下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗Y(吨标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1) 请画出上表数据的散点图；
(2) 请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
；
(3) 已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性
同归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值：3×2.5+4×3+5×4+6×4.5=66.5。参考公式：用最小二乘法求线性同归方程系数公式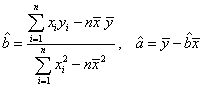
)
16. 观察和探究：
(1)观察下列各组数据并填空
A．1 2 3 4 5 
____________,
_____________;
B. 11 12 13 14 15 
____________,
_____________;
C. 10 20 30 40 50 
____________,
_____________;
D. 3 5 7 9 11 
____________,_____________;
(2)分别比较A和B、C、D的结果，你能发现什么规律？
(3)若已知一组数据
的平均数为
，方差为
，求另一组数据
的平均数和方差.
17.定义:点
与直线
的“纵向距离”为
.
已知
三点,存在直线
，使
三点到直线的“纵向距离的平方和”
最小,（1）求直线的方程和的最小值.（2）判断点
与直线的位置关系.
18．某旅游商品生产企业，2007年某商品生产的投入成本为1元/件，出厂价为流程图的输
出结果
元/件，年销售量为10000件，因2008年国家长假的调整，此企业为适应市场需求，计划提高产品档次，适度增加投入成本．若每件投入成本增加的比例为
（
），则出厂价相应提高的比例为
，同时预计销售量增加的比例为
．已知得利润
（出厂价
投入成本）
年销售量．
（1）写出2008年预计的年利润
与投入成本增加的比例的关系式；
（2）为使2008年的年利润比2007年有所增加，问：投入成本增加的比例应在什么范围内？
 |
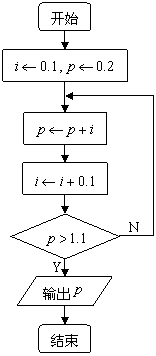第四周训练题：算法与统计答案
一、选择题
1. D 2. A 3. B 4. C 5. C 6. A 7. D 8. B
二、填空题
9.
4 人 10. 785，667，199，507，175 11. 
12.
S=3 3 13. 0.38
三、解答题
14. 解：（1）
| 分组 | 频数 | 频率 |
|
| 2 | 0.2 |
|
| 3 | 0.3 |
|
| 4 | 0.4 |
|
| 1 | 0.1 |
| 合计 | 10 | 1.0 |
（2）图略，在
中的比率是0.7
（3）8辆
（4）丛数： 13.75 中位数： 13.45 平均数：13.41
15.解：（1）图略
（2）经计算 
（3）当
时，
，降低了标准煤
吨
16.解：（1）A. 
B. 
C．
D．
（2）规律：如果样本
的平均数为
，方差为，则样本
的平均数为
，方差为
（3）由（2）知，
，所以这组数据的平均数是
，方差为
17.解：（1）
当
时，
即
（2）点D在直线上
18.解：（1）由框图知 
元
所以 
即 
（2）2007年利润为
元
令 
得
