_____班；姓名______
学号__________ 高一第二学期·必修三之算法初步单元测试
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
1．将两个数
交换,使
,下面语句正确一组是 ( )
|
|
|
|
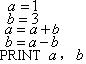
2题．计算机执行左边的程序段后，输出的结果是（ ）
A．
B．
C．
D．
3．当
时，下面的程序段输出的结果是（ ）
A．
B．
C．
D．
4．用“辗转相除法”求得
和
的最大公约数是（ ）
A． B． C．
D．
5．当
时，下面的程序段执行后所得的结果是 ( )
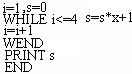A．
B．
C．
D．
6. 把89化为五进制数，则此数为 ( )
A. 322(5) B. 323(5) C. 324(5) D. 325(5)
7．用秦九韶算法求多项式f（x）=12+35x－8x2+79x3+6x4+5x5+3x6在x=－4的值时，v4的值为（ ）
A.－57 B. －845 C. 220 D .3392
8．读程序
甲：INPUT i=1 乙：INPUT I=1000
S=0 S=0
WHILE i≤1000 DO
S=S+i S=S+I
i=i+l I = I一1
WEND Loop UNTIL I<1
PRINT S PRINT S
END END
对甲乙两程序和输出结果判断正确的是 ( B )
A．程序不同结果不同 B．程序不同，结果相同
C．程序相同结果不同 D．程序相同，结果相同
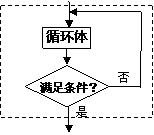
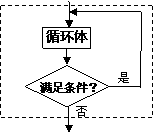
9．在下图中，直到型循环结构为（ ）
A． B． C． D
10．阅读下列程序：
输入x；
if x＜0， then y ＝
；
else
if x ＞0， then y ＝
；
else y＝0；
输出 y． 如果输入x＝－2，则输出结果y为( )
A．
－5
B． －－5
C． 3＋
D． 3－
二 填空题
11题．用“秦九韶算法”计算多项式
，当x=2时的值的过程中，要经过 次乘法运算和
次加法运算。
12题．下列各数
、 
、 
、 
中最小的数是___
13题．下面的程序输出的结果
=
14题. 右边面的程序运行后的结果为__________
（其中：“（a+j） mod 5”表示整数(a+j)除以5的余数）
15题. 程序框图如下：
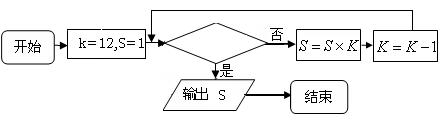
如果上述程序运行的结果为S＝132，那么判断框中应填入
三、解答题
16题．把“五进制”数
转化为“十进制”数，再把它转化为“八进制”数。
17题．用秦九韶算法求多项式
当
时的值。写出其算法,写出相应的程序语句.
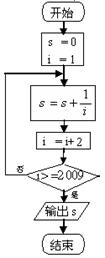
18．设计一个算法求：
；试用流程图和相应程序表示．
19题:. 写出用二分法求方程x3－x－1=0在区间［1，1.5］上的一个解的算法（误差不超过0.001），并画出相应的程序框图及程序.
20. 修订后的《中华人民共和国个人所得税》法规定，公民全月工资、薪金所得税的起征点为1600元，即月收入不超过1600元，免于征税；超过1600元的按以下税率纳税；超过部分在500元以内（含500元）税率为5％，超过500元至2000元的部分（含2000元）税率为10％，超过2000元至5000元部分，税率为15％，已知某厂工人的月最高收入不高于5000元。
（1）请用自然语言写出该厂工人的月收入与应纳税款的一个算法（不要写成程序框图或计算机程序）；
(2）将该算法用程序框图描述之。 (3) 写出相应的计算机程序
21. 中国网通规定：拨打市内电话时，如果不超过3分钟，则收取话费0.22元；如果通话时间超过3分钟，则超出部分按每分钟0.1元收取通话费，不足一分钟按以一分钟计算。设通话时间为t（分钟），通话费用y（元），如何设计一个程序，计算通话的费用。
参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | D | C | C | C | B | A | D |
11题． 5次乘法和5次加法; 12题、
13题、17； 14题、0； 15题、
或
解: 或 .解析：第一次循环时S→1×12=12,
K→12-1=11, ；第二次循环时，S→12×11=132，K→11-1=10；此时S=132是题目中程序运行的结果，因此，循环必须终止；所以判断框中应填入的为“K≤10？”。
16题．解：
17题．解：
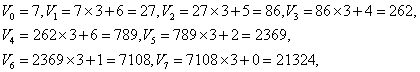
18题解：流程图如下： 相应程序如下：
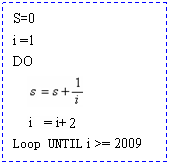
19题解、
程序：a=1
b=1.5
c=0.001
DO
x=（a+b）/2
f（a）=a∧3－a－1
f（x）=x∧3－x－1
IF f（x）=0 THEN
PRINT “x=”；x
ELSE
IF f（a）*f（x）＜0 THEN
b=x
ELSE
a=x
END IF
END IF
LOOP UNTIL ABS（a－b）＜=c
PRINT “方程的一个近似解x=”；x
END
20题解：（1）算法:
第一步 输入工资x (注x<=5000);
第二步 如果x<=1600,那么y=0;如果1600<x<=2100,那么 y=0.05(x-1600);
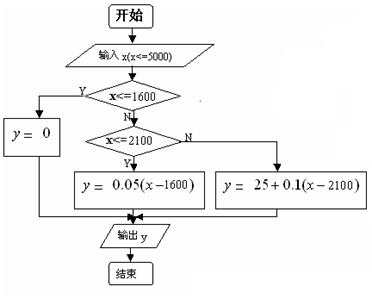否则 y=25+0.1(x-2100)
第三步 输出税款y, 结束。
（2）程序框图为：
（3）INPUT x （x<=５０00）
IF x<=1600 THEN y =0
ELSE IF x<=1600 THEN y =0.05*(x－1600)
ELSE y=25+0.1(x-2100)
END IF
END IF
PRINT y
END
21题解：算法分析：数学模型实际上为：y关于t的分段函数。关系式如下：
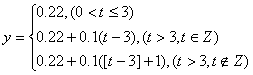
其中[t－3]表示取不大于t－3的整数部分。
算法步骤如下：
第一步：输入通话时间t；
第二步：如果t≤3，那么y = 0.22；否则判断t∈Z 是否成立，若成立执行
y= 0.2+0.1× (t－3)；否则执行y = 0.2+0.1×（ [t－3]+1）。
第三步：输出通话费用c 。
算法程序如下：
INPUT “请输入通话时间：”；t
IF t<=3 THEN
y=0.22
ELSE
IF INT(t)=t THEN
y=0.22+0.1*(t－3)
ELSE
y=0.22+0.1*(INT(t－3)+1)
END IF
END IF
PRINT “通话费用为：”；y
END