高一下数学测试卷(4)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确的答案填在指定位置上.)
1. 函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 若角![]() 满足
满足![]() ,则
,则![]() 是( )
是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
3. 若点![]() 是角
是角![]() 终边上的一点,且满足
终边上的一点,且满足![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 设![]() ,且
,且![]() ,则
,则![]() 可以是( )
可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5. 满足![]() 的一个取值区间为( )
的一个取值区间为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
6. 设![]() ,则下列不等式中一定成立的是:( )
,则下列不等式中一定成立的是:( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7. ![]() 中,若
中,若![]() ,则
,则![]() 一定是( )
一定是( )
A.钝角三角形 B. 直角三角形
C.锐角三角形 D.以上均有可能
8. 已知![]() 为第一象限角,若将角
为第一象限角,若将角![]() 的终边逆时针旋转
的终边逆时针旋转![]() ,则它与单位圆的交点坐标是( )
,则它与单位圆的交点坐标是( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
9. 当![]() 时,函数
时,函数![]() 的最小值为( )
的最小值为( )
A.![]() B.3
C.
B.3
C.![]() D.4
D.4
10.在平面直角坐标系中,横、纵坐标均为整数的点叫做格点. 若函数![]() 的图象恰好经过
的图象恰好经过![]() 个格点,则称函数
个格点,则称函数![]() 为
为![]() 阶格点函数. 下列函数中为一阶格点函数的是 ( )
阶格点函数. 下列函数中为一阶格点函数的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共计100分)
二、填空题(本大题共5小题,每小题5分,共25分,把正确的答案填在指定位置上.)
11.函数![]() 的定义域是
的定义域是
12.若![]() 是方程
是方程![]() 的解,其中
的解,其中![]() ,则
,则![]() =
=
13.函数![]() 的单调递减区间为
的单调递减区间为
14.函数![]() 的值域为______________
的值域为______________
15.设集合![]() ,
, ![]() . 给出
. 给出![]() 到
到 ![]() 的映射
的映射![]() . 关于点
. 关于点![]() 的象
的象![]() 有下列命题: ①
有下列命题: ①![]() ;
;
②其图象可由![]() 向左平移
向左平移![]() 个单位得到;
个单位得到;
③点![]() 是其图象的一个对称中心
是其图象的一个对称中心
④其最小正周期是![]()
⑤在![]() 上为减函数
上为减函数
其中正确的有
三.解答题(本大题共5个小题,共计75分,解答应写出文字说明,证明过程或演算步骤.)
16. (本题满分12分)已知函数![]() ,求
,求![]() 的最大值与最小值,并分别写出取最大值与最小值时自变量
的最大值与最小值,并分别写出取最大值与最小值时自变量![]() 的集合。
的集合。
17. (本题满分12分)已知![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的值.
的值.
18. (本题满分12分)已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;
(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
19. (本题满分12分)已知函数![]()
(1)求![]() 的定义域并判断它的奇偶性;
的定义域并判断它的奇偶性;
(2)求![]() 的值域.
的值域.
20.(本题满分13分)关于函数![]() 的性质叙述如下:①
的性质叙述如下:①![]() ;②
;②![]() 没有最大值;③
没有最大值;③![]() 在区间
在区间![]() 上单调递增;④
上单调递增;④![]() 的图象关于原点对称.问:
的图象关于原点对称.问:
(1)函数![]() 符合上述哪几条性质?请对照以上四条性质逐一说明理由.
符合上述哪几条性质?请对照以上四条性质逐一说明理由.
(2)是否存在同时符合上述四个性质的函数?若存在,请写出一个这样的函数;若不存在,请说明理由.
21. (本题满分14分)已知定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,且在
,且在![]() 上是增函数. 又函数
上是增函数. 又函数![]()
(1)证明:![]() 在
在![]() 上也是增函数;
上也是增函数;
(2)若![]() ,分别求出函数
,分别求出函数![]() 的最大值和最小值;
的最大值和最小值;
(3)若记集合![]() ,
,![]() ,求
,求![]() .
.
参考答案(理)
一、选择题:DADCC BADBA
二、填空题:11 ![]() 12
12 ![]()
13 ![]() 14
14 ![]() 15 ①④⑤
15 ①④⑤
1.D解析:![]()
2.A解析:由![]() 得,
得,![]() ,故
,故![]() 是第一象限角。
是第一象限角。
3.D解析:由题![]() 且
且![]() ,得
,得![]() ,故
,故![]() .
.
4.C解析:由题得![]() ,故
,故![]() 可以是
可以是![]() .
.
5.C解析:根据![]() ,易知
,易知![]() 满足题意.
满足题意.
6.B解析:当![]() 时,四个均成立. 当
时,四个均成立. 当![]() 时,
时,![]() ,此时
,此时
只有![]() 成立.
成立.
7.A解析:因![]() 即有
即有![]() . 由
. 由![]() ,得
,得
![]() 即
即![]() ,故
,故![]()
8.D解析:此时角变为![]() , 则它与单位圆的交点坐标为(
, 则它与单位圆的交点坐标为(![]() ),即为(
),即为(![]() )
)
9.B解析:由![]() ,整理得
,整理得![]() .
.
令![]() ,则函数
,则函数![]() 在
在![]() 时有最小值3.
时有最小值3.
10.A解析:选项A:由![]() ,
,![]() 知
知
函数![]() 的格点只有
的格点只有![]() ;
;
选项B:由![]() ,
,![]()
![]()
![]() ,故函数
,故函数![]() 图象没有经过格点;
图象没有经过格点;
选项C:形如![]() 的点都是函数
的点都是函数![]() 的格点;
的格点;
选项D:形如![]() 的点都是函数
的点都是函数![]() 的格点.
的格点.
11.![]() 解析:
解析:![]() 或
或![]() ,
,![]() .
.
12.![]() 解析:由
解析:由![]() ,
,![]() 或
或![]()
![]() ; 又
; 又![]() , 知
, 知![]() .
.
13. ![]() 解析:找原函数的递减区间,即找
解析:找原函数的递减区间,即找![]() 的递增区间,且使
的递增区间,且使![]()
![]()
14. ![]() 解析:
解析:![]()
15.①④⑤ 解析:点![]() 的象
的象![]()
故①④⑤均为真命题.
16.解析:![]()
![]()
![]()
当![]() 时,
时,![]() 取最小值
取最小值![]() ;当
;当![]() 时,取最大值
时,取最大值![]() ,
,
17.解析:(1)由![]() 知,
知,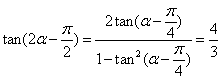 ,即
,即![]()
![]() ,又
,又![]() ,可得
,可得![]()
(2)由![]() 知,
知,![]()
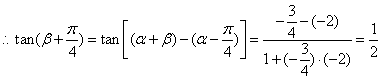
18.解析:(1)由题,![]()
![]()
所以函数![]() 在
在![]() 上的单调增区间为
上的单调增区间为![]() ,
,![]()
(2)当![]() 时,
时,![]() 单增,
单增,![]() 时,
时,![]() 取最小值
取最小值![]() ;
;![]() 时,
时,![]()
取最大值![]() .
.
由题意知,![]()
所以实数![]() 的范围是
的范围是![]()
19.解析:(1)![]() 即
即![]()
故![]() 的定义域为
的定义域为![]()
![]() 的定义域关于原点对称,且
的定义域关于原点对称,且![]()
![]() ,故
,故![]() 为偶函数.
为偶函数.
(2)当![]() 时,
时,
![]()
![]() 又
又![]() 故
故![]() 的值域为
的值域为![]() .
.
20.解析:(1)函数![]() 符合性质②③.
符合性质②③.
①![]()
![]() 不一定等于
不一定等于![]() ;
;
②令![]() ,此时
,此时![]() ,另
,另![]() ,则
,则![]()
故![]() 没有最大值;
没有最大值;
③函数![]() 和
和![]() 在
在![]() 在均为大于0,且都是单调递增.
在均为大于0,且都是单调递增.
故函数![]() 在
在![]() 上单调递增;
上单调递增;
④![]() 的定义域是
的定义域是![]() ,
,![]()
所以![]() 的图象关于y轴对称.
的图象关于y轴对称.
(2)存在同时符合上述四个性质的函数.
例如:函数![]() ;函数
;函数![]() 等.(答案不唯一)
等.(答案不唯一)
21解析:(1)证明:任取![]() ,则
,则![]()
且![]() 在
在![]() 上是增函数,
上是增函数,![]() .又
.又![]() 为奇函数,
为奇函数,
故![]()
即![]() ,
,![]() 在
在![]() 上也是增函数.
上也是增函数.
(2)由![]() ,
,
令![]() ,则
,则![]() ,记
,记![]() ,由
,由![]() 知,
知,![]()
函数![]() 在
在![]() 上是减函数,
上是减函数,
故![]() 时,
时,![]() 有最大值
有最大值![]() ;
;![]() 时,
时,![]() 有最小值
有最小值![]() .
.
(3)由![]() 在
在![]() ,
,![]() 上是增函数,
上是增函数,![]()
![]() 或
或![]() ,又
,又![]() ,
,
所以![]() ,
,
即![]() 对
对![]() 恒成立.
恒成立.
![]()
![]() ,
,![]()
当![]() 时取得.
时取得. ![]()
即![]() , 故
, 故![]() .
.