高一下数学测试卷(3)
黄冈中学 胡华川 2008.3.9
一. 选择题(本大题共10小题,每小题5分,共50分)
1.已知![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知锐角![]() 终边上一点P的坐标为(
终边上一点P的坐标为(![]() ),则
),则![]() 的弧度数为
的弧度数为
A.![]() B.
B.![]() C.3 D.以上均不对
C.3 D.以上均不对
4.已知![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() 2 C.2 D.
2 C.2 D.![]()
![]()
5.设![]() ,如果
,如果![]() 且
且![]() ,那么
,那么![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.若![]() ,则
,则![]() 的值等于
的值等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.化简![]() 的结果为
的结果为
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
8.设![]() 若
若![]() ,则
,则![]() 的值为
的值为
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
9..已知奇函数![]() 单调减函数,又α,β为锐角三角形内角,则(
)
单调减函数,又α,β为锐角三角形内角,则(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知α为第二象限角,且![]() 则m的允许值为
则m的允许值为
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]() 或
或![]()
二.填空题:本大题共5小题,每小题5分,共25分.把答案填在题中横线上.
11.已知![]() ,则
,则![]() 的值为_________.
的值为_________.
12.已知![]() ,则
,则![]() __________.
__________.
13.已知等腰![]() 的腰为底的2倍,则顶角
的腰为底的2倍,则顶角![]() 的正切值是____________.
的正切值是____________.
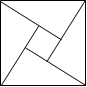 14. 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽 的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为
14. 2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽 的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,那么
,那么![]() 的值等于 .
的值等于 .
15.已知![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,
则![]() 的为__________.
的为__________.
答题诚信度________% 班级__________ 座号_________ 姓名________________ 分数_____________
答 题 卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 11 | 12 | 13 | 14 | 15 | |||||
| 答案 | ||||||||||
三.解答题:本大题共6小题,共75分.解答应写出文字说明或演算步骤.
16.(本小题12分)化简求值:
(1)![]() ;
;
(2)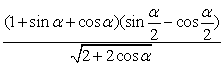 (
(![]() ).
).
17.(本小题12分) 已知![]() <
<![]() <
<![]() <
<![]() ,
,
(1)求![]() 的值; (2)求
的值; (2)求![]() 的值.
的值.
18.(本小题12分)已知函数![]()
(1)当![]() 时,求
时,求![]() 的最大值和最小值;
的最大值和最小值;
(2)求![]() 的范围,使
的范围,使![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
19.(本小题12分)设![]() 满足
满足![]() ,
,
(1)求![]() 的表达式; (2)求
的表达式; (2)求![]() 的最大值.
的最大值.
20.(本小题13分)水渠横断面为等腰梯形,渠深为h,梯形面积为S. 为了使渠道的渗水量达到最小,并降低成本,应尽量减少水与水渠壁的接触面. 问此时水渠壁的倾斜角α应是多少?
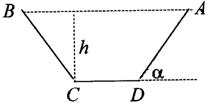
21.(本小题14分)在![]() 中,已知三个内角A、B、C满足关系式
中,已知三个内角A、B、C满足关系式
![]() ,
,
(1)若任意交换A、B、C的位置,![]() 的值是否变化?并证明你的结论;
的值是否变化?并证明你的结论;
(2)试求![]() 的最小值.
的最小值.
当且仅当![]() 时取到等号.
时取到等号.
黄冈中学高一下数学测试卷(3)参考答案
一.选择题 AABCC DBACC
二.填空题 11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.
15.![]()
答案提示:
1.解析:由![]() 得
得![]() ,
,![]()
![]() .
.
2.解析:在![]() 中
中![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
3.解析:![]() ,而
,而![]() ,所以
,所以![]()
4.解析:由已知得![]() ,
,![]()
6.解析:由![]() 得
得![]() ,
,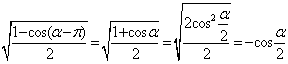
7.解析:原式![]()
8.解析:令![]() ,则
,则![]() ,所以
,所以![]() ,解得
,解得![]() .
.
9.解析:由题意知![]() 单调减函数,又
单调减函数,又![]() ,
,![]()
![]() ,
,
![]()
![]() ,所以
,所以![]() .
.
10.解析:由题意得: ![]() ,解得
,解得![]() 或
或![]() ,
,
又![]() ,所以舍去
,所以舍去![]() ,取到
,取到![]() .
.
11.解析:![]()
![]()
12.解析:易知:![]() 以
以![]() 为周期,
为周期,![]() ,
,
![]()
![]() =
=![]()
13.解析:易知![]() ,
,![]()
![]() ,
,![]() ,
,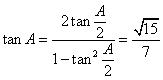 .
.
15.解析:由题意得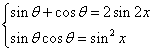 ,
,![]()
![]() ,化简得
,化简得
![]() ,解得
,解得![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]()
三.解答题
16.解:(1)原式
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)原式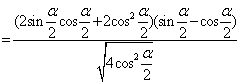
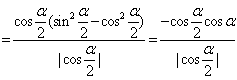
![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() 原式
原式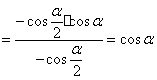
17.解:(1)由![]() ,得
,得![]() ;∴
;∴![]() ,于是
,于是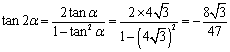 ;
;
(2)由![]() ,得
,得![]() ;又∵
;又∵![]() ,∴
,∴![]() ;由
;由![]() 得:
得:![]()
![]()
![]() , 所以
, 所以![]()
18.解:(1)![]() ,由
,由![]() ,
,
所以当x=-![]() 时,f(x)有最小值-
时,f(x)有最小值-![]() ,当x=
,当x=![]() 时,f(x)有最大值-
时,f(x)有最大值-![]() .
.
(2)![]() 的对称轴为
的对称轴为![]() .又f(x)在
.又f(x)在![]() 上是单调函数,则
上是单调函数,则![]() .
.
![]() .故所求θ的范围是
.故所求θ的范围是![]()
19.解:(1)由![]() ①
①
得![]() ② 由3
② 由3![]() ①-②得
①-②得![]()
又![]() ,所以
,所以![]() ,故
,故![]() (
(![]() ).
).
(2)对![]() ,将函数
,将函数![]() 的解析式变形,得
的解析式变形,得
![]()
![]() =
=![]() , 当
, 当![]() 时,
时,![]()
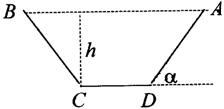 20.解: 设
20.解: 设![]() ,
,
![]() ,
,
![]() ,
,
设![]()
记![]()
![]()
![]() ,等号成立时,
,等号成立时,![]()
21.解: (1)![]()
![]()
![]() 所以任意交换A、B、C的位置,
所以任意交换A、B、C的位置,![]() 的值不会变化.
的值不会变化.
(2)![]() 角A、B、C任意交换性,不妨设
角A、B、C任意交换性,不妨设![]() 锐角,则
锐角,则![]() ,
,![]() ,
,
![]()
![]()
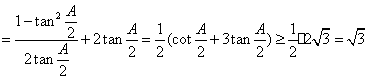
当且仅当![]() 取到等号。
取到等号。