高一元旦竞赛数学试题

高一元旦竞赛数学试题

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至6页，共6页。共150分，考试时间120分钟。

注意事项：

1.　　 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试卷类型（A或B）用铅笔涂在答题卡上。

2.　　　 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上。

3.　　　 考试结束将本试卷和答题卡一并收回。

一.选择题（本大题共12小题，每小题5分，共60分）

1.以下命题正确的是　 （　　　 ）

A　直角三角形绕其一边所在直线旋转得到的旋转体是圆锥

B　夹在圆柱的两个平行截面间的几何体还是圆柱

C　圆锥截去一个小圆锥后剩余部分是圆台

D　棱锥截去一个小棱锥后剩余部分是棱台

2.以下不属于三视图的是　（　　 ）

A　正视图　B　侧视图　C　后视图　D　俯视图

3.已知三角形ABC是边长为2a的正三角形，那么它的平面直观图的面积是　（　　 ）

A ²　 B ²　 C　²   D　a²

4.圆柱的一个底面积为S，侧面展开图是一个正方形，那么这个圆柱的侧面积是（　　 ）

A　4S　 B2S　　CS　　DS

5.已知长方体一个顶点上三条棱的长分别是3、4、5，且它的顶点都在同一球面上，则这个球的表面积是（　　  ）

A　20　 B　25　C  50　　D 200

6.设正方体的表面积为24cm ²,一个球内切于该正方体，那么这个球的体积是（　　 ）

A　 cm³　 B 6cm³　C   cm³　　D　 cm³

7.如果直线a面a,直线b面a,直线L直线a=A，直线Lb=B,那么下列关系成立的是（　　　 ）

A　 L a　　B　L a　 C　La=A　　D　LA=B

8.空间中有五个点，其中有四个点在同一平面内，但没有任何三点共线，这样的五个点确定的平面最多可以是 （　　 ）

A　4个　 B　5个　　C　6个　　D　7个

9.一条直线与两条平行线中的一条成为异面直线，则它与另一条（　　）

A　相交　 B　异面　 C　 相交或异面　　D　平行

10.将棱长为1的正方体加工成一个体积最大的球，那么球的体积为（　　）

A、　　 B、　 　 C、 　 D、　

11.64个直径为的小球，记它们的体积和为V，表面积和为S，一个直径为a 的小球，记其体积为V´，表面积为S´，则 （　　 ）

A　V>V´ ，S>S´　B V<V´ ，S<S´　C V=V´ ，S>S´　D V=V´ ，S=S ´

12.一个正四棱台边长分别为m .n,侧面积等于两个底面积之和，则这个棱台的高为（　　 ）

A　　B　 　C　 　　D　

数 学 试 题

第Ⅱ卷（非选择题，共56分）

注意事项：

　　1. 第Ⅱ卷共4页，用钢笔或圆珠笔直接答在试题卷中。（除题目有特殊规定外）

　  2. 答卷前将密封线内的项目填写清楚。

二.填空题（本大题共4小题，每小题4分，共16分）

13.两个平面可将空间分成　　　　　　　　　 部分。

14.正方体ABCD—A`B`C`D`中，E为DD`的中点，则BD`与平面ACE的位置关系是　　 　　　　　。

15.正方体ABCD—A`B`C`D`中，AB的中点为M，DD`的中点为N，则异面直线B`M与CN所成的角的大小　　　　　　 。

16.P是△ABC所在平面外一点，平面a∥平面ABC，a交线段PA.PB.PC于A`.B`.C`，若PA`：AA`=2：3，则△A`B`C`与△ABC的面积比等于　　　 。

三.解答题（本大题共6小题，共74分）

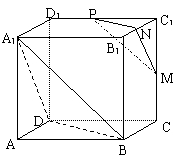17.如图，在正方体ABCD—A₁B₁C₁D₁中，M,N,P分别是C₁C,B₁C₁,C₁D的中点，求证：平面MNP∥平面A₁BD。

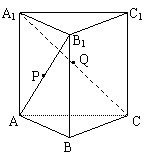18.在三棱柱ABC-A₁B₁C₁中,P，Q分别是AB₁与A₁C的中点，如图

求证：PQ∥面ABC

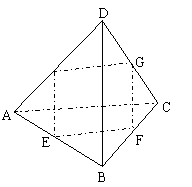19、如图，空间四边形ABCD中，E，F，G分别是AB，BC，CD的中点，求证：（1）BD∥平面EFG；（2）AC∥平面EFG。

20、有一个底面半径和高都是R的圆锥形密闭容器，容器中装有一些水。如果底朝下（且水平）时水的高度为1／2R，那么当底面朝上（且水平）时容器中水的高度为多少?

21、一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为r的铁球，这时水面恰好与球的上面相切，将球从圆锥内取出后，求圆锥内的水深。

　　　　　　　

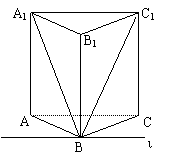22、在三棱柱ABC-A₁B₁C₁中过A₁C₁及点B的平面交下底面ABC所在的平面于l，试判断A₁C₁与l的位置关系，并证明之。

参考答案

一、选择题

 1.C 2、C 3、C 4、A 5、C 6、D 7、A 8、D 9、C 10、B 11、C 12、A

二、填空题

13、2或4　14、平行　15、90⁰　16、4：25

三、解答题

17、　　　 连结B₁D₁,B₁C

PN∥B₁D_1,

 BD∥B₁D₁ PN∥BD　

 A₁D∥B₁C　

MN∥B₁C　　　　MN∥A₁D

　　　　　　  PN面PMN　　　　　　 PN∥面A₁DB

　　　　　　　PN面A₁DB

BD面A₁DB　　　　　　　　　　　　　　

同理　　　　　　　　　　　　　　　 MN∥A₁DB　　　　　　　　　　

PNMN=N

面MNP∥面A₁DB

18、　　　 连结A₁B

∵A₁B₁BA为平行四边形，P为AB₁的中点

∴A₁BAB₁=P

∴P为A₁B的中点

又∵Q为A₁C的中点

∴PQ∥BC

又∵PQ面ABC

BC面ABC

∴PQ∥面ABC

19、　　　 （1）连结EF,FG

　　　∵E、F、G分别是AB、BC、CD的中点

∴FG∥BD

又∵FG面EFG，BD面EFG

∴BD∥面EFG

（2）同理AC∥面EFG

20、　　　 ∵V_SO=1／3∏R²R=∏／3　R³

　 ∴V_O1O=7／24　∏R³

V_SO1=1／3　∏h².h=1／3　∏h³

V_SO1=V_OO1=7／24　∏R³

∴h=　R

21、答案详见学案

22、A₁C₁∥l

证明∵A₁C₁∥AC

A₁C₁面ABC

AC面ABC

∴A₁C₁∥面ABC

又∵A₁C₁∥面A₁C₁B

面A₁C₁B₁面ABC=l

∴A₁C₁∥l