高一数学上学期期中考试
数 学 试 题
一、选择题（本题共10小题，每题5分，共50分，请将答案填在答题卷上）
1．若 
，则下面成立的是
A．
B．
C．
D．
2．设集合
，若
，则
A．
B．
C．
D．
3．已知集合
，
，
，
，那么集合P的子集的个数为
A．3 B．7 C．8 D．16
4．设M、P是两个非空集合，我们规定：
，根据这一规定，
等于
A．
B．
C．M
D．P
5．已知真命题：“
”和“
”，那么“
”是“
”的
A．充分非必要条件 B．必要非充分条件
C．充分必要条件 D．既不充分也不必要条件
6．已知函数
在［3，+∞）上为增函数，则m的取值范围是
A．（－∞，－2） B．（－3，－2）∪（2，+∞）
C．（－3，－2） D．（2，+∞）
7．设
，不等式
恒成立，则实数k的取值范围是
A．［0，+∞） B．［0，+∞） C．［0,1］ D．（－1,3）
8．函数
的
A．最小值为0，最大值为4 B．最小值为－4，最大值为4
C．最小值为－4，最大值为0 D．最小值和最大值都不存在
9．已知函数
的反函数
的定义域为［0,1］，那么函数
的值域是
A．
B．［－1,0］ C．［0,1］
D．R
10．若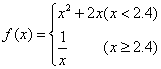
，则
的值为
A．1
B．
C．
D． 2
二、填空题（本题共5小题，每题5分，共25分，请将答案填在答题卷上）
11．调查100名携带药品出国的旅游者，其中75人带有感冒药，80人带有胃药，那么既带有感冒药又带有胃药的人数最多有 人，最少有 人。
12．二次函数
的部分对应值如下表：
|
| －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 |
|
| 6 | 0 | －4 | －6 | －6 | －4 | 0 | 6 |
则不等式
的解集为
13．若函数
在［0，+∞）上为增函数，则实数a、b的取值范围是 。
14．若
是二次函数，
对任意实数x都成立，又知
，
则
.（填大小关系）
15．已知函数满足：对任意实数
，当
时，有
，且
，则
。（请写出一个满足这些条件的函数即可）
三、解答题（本题共6小题，共75分，请将答案写在答题卷上）
16．（本题满分12分）设方程
的解集为A，方程
的解集为B，已知
，
，试求出实数
的值。
17．（本题满分12分）已知函数是定义在
上的减函数，且有
，若
，求实数
的取值范围。
18．（本题满分12分）已知关于
的方程
，求方程至少有一个负根的充要条件。
19．（本题满分12分）若函数
的值域是
，求的定义域。
20．（本题满分13分）已知△ABC是边长为2 的正三角形，P为AB的中点，动点Q由B点出发，经BC、CA运动到A，设Q所走的路程为x，以PQ为边长的正方形面积为y，则y是x的函数。
⑴试求这个函数的解析式；
⑵写出这个函数的增、减区间。
21．（本题满分14分）设函数
，
，且方程
有实根。
⑴证明：
且
⑵若是方程的一个实根，判断
的正负并加以证明。
数 学 试 题
一、选择题（本题共10小题，每题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（本题共5小题，每题5分，共25分）
11_______________12._______________13.________________
14.______________ 15.___________________
三、解答题（本题共6小题，共75分）
 |
|
 | |||||
| |||||
 | |||||
数 学 试 题 答 案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | C | A | A | B | C | B | C | A |
二、填空题
11. 75，55 12. （－∞，－2）∪（1，+∞）13 
且
14. ＞ 15. 
三、解答题
16.
17.解：∵
，则有
又∵是定义在上的减函数，∴满足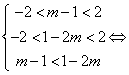
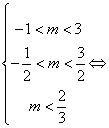
∴的取值范围是
18.解：当
时，方程即为
符合题意；
当
≠6时先求方程无负根的条件⑴方程无实根
解得
⑵方程有二非负实根，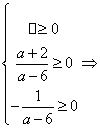
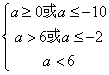解得
综合⑴⑵知，当≠6时，方程无负根的条件是＜2，∴方程至少有一负根的条件是≥2
19.解：
，显然函数在
上单调递减；由题意可得
解得
所以的定义域为
20.⑴从题中可知当
时
.当
时
即
∴函数的解析式为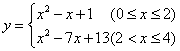
⑵此函数的递增区间为
，
.递减区间为
，
21.解：⑴由，知
∴
又∵
，故
，∴
.又∵有实根，即
有实根，故
，即
，∴
或
，由题设条件知得，由知
⑵∵
且
∴
∴
∴
即的符号为正。