高一数学上学期期末模拟试题
一、填空题(每小题5分,共计70分)
1. 设全集
，则
= ▲ .
2. 函数
的值域为 ▲ .
3. 半径等于
，圆心角为
的扇形的周长是 ▲
cm.
4. 设
则
▲ .
5. 函数
(
)的单调增区间是 ▲
.
6. 函数
,
的图象必经过定点 ▲
.
7. 计算：
+(lg2)3+(lg5)3+3lg2·lg5 
▲ .
8. 已知
,且
，则
▲
.
9. 若关于x的方程
的两实根
满足
，则实数
的取值范
围是 ▲ .
10. 若函数
= 
+
是其定义域上的奇函数，则实数值是 ▲ .
11. 根据表格中的数据，可以判定方程ex-x-2=0的一个根所在的区间为 ▲
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
12. 在△ABC中，点
分别在线段
上,且
，记
=
，
，
则
▲
. (用
表示)
13. 下列几种说法:(1)所有的单位向量均相等;(2)平行向量就是共线向量;(3)平行四边形
中,一定有
;(4)若
,则
;其中所有的正确的说法的序号是 ▲ .
14．记集合
.例如
,则
有
. 现已知
,则集合
▲ .
二、解答题(共计90分)
15．已知集合
,
(1)若
，求实数
的取值范围; (2)若
, 求实数的取值范围。
16. 已知函数
,
(1) 求函数的最小正周期和初相;
(2) 先将函数的图象上各点向右平移
个单位,再保持各点的纵坐标不变,横坐标变为
原来的2倍得到函数
的图象,求的解析式;
(3) 在(2)的条件下,求函数
的值域.
17. 季节性服装当季节即将来临时，价格呈上升趋势，设某服装开始时定价为10元，并且每
周(7天)涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直到16周末，该服装已不再销售.
(1)试建立价格P与周次t之间的函数关系式.
(2)若此服装每件进价
与周次t之间的关系为
，
试问该服装第几周每件销售利润L最大?(注：每件销售利润＝售价－进价)
18. 已知向量
,向量
与
的夹角为
,且
,(1)求向量 (2)若向量与向
量
的夹角为
,而向量
,其中
,试求
的取值范围.
19.已知向量
(1)求证：
；
(2)若存在不等于
的实数
和
，使
满足
。试求此时
的最小值。
20. 已知函数的定义域
，且对于任意
，均有
,且当
时，
;
(1)求
与
的值；
(2)判断函数的奇偶性并证明；
(3)求证:在
上是增函数； (4)若
，解不等式
。
数 学 最 后 一 考
班级： 学号： 姓名：
一、填空题：(每题5分，共70分)
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
三、解答题：(共90分)
| 15.解： |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 16．解： |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 17．解： |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 18．解： |
|
|
|
|
|
|
| 19．解： |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20.解: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
数 学 最 后 一 考 答案
1. 
2. 
3. 
(多写cm不扣分)
4. 
5. 
6. 
7. 5
8. 
9. 
10.1
11. (1,2)
12. 
13. (2) (3)
14. 
15. (1) 
(2) 
16. (1) 
(2) 
(3) 
,令
,
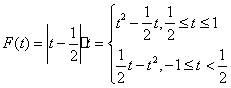
值域
17..解：(1)P＝
(2)因每件销售利润＝售价－进价，即L＝P－Q
故有：当t∈［0，5］且t∈N*时，L＝10＋2t＋0.125(t－8)2－12＝
t2＋6
即，当t＝5时，Lmax＝9.125
当t∈(5，10］数时t∈N*时，L＝0.125t2－2t＋16
即t＝6时，Lmax＝8.5
当t∈(10，16］数时，L＝0.125t2－4t＋36
即t＝11时，Lmax＝7.125
由以上得，该服装第5周每件销售利润L最大
18.(1)
(2)
19. 解：由诱导公式得： 
…………2分
（1）
， 则 
………………………5分
（2）
………………7分
即：
，
…………………10分
即当
时，
的最小值为
. ………………14分
20. 解:（1）令x1=x2=1，有f(1×1)=f(1)+f(1)，解得f(1)=0。 2分
令x1=x2=-1，有f[(-1)×(-1) ]=f(-1)+f(-1)=f(1)=0，解得f(-1)=0。 4分
（2）令x1=-1，x2=x，有f(-x)=f(-1)+f(x)=f(x)，∴f(x)是偶函数。 8分
（3）设x1,x2∈(0,+∞)且x1<x2，则
，
，
则
，∴f(x)在区间(0,+∞)上是增函数。 12分
（4）f(16)=f(4×4)=f(4)+f(4)=2，由f(3x+1)≤2变形为f(3x+1)≤f(16)。
∵f(x)为偶函数，∴f(-x)=f(x)=f(x)，在（3）的条件下有f[3x+1]≤f(16)
∴3x+1≤16且3x+1≠0，解得
.
16分