高一数学上学期期末综合试题
数 学
一、填空题
1.已知向量![]() 的值是 .
的值是 .
2.函数y=sin(2x+)图象的对称中心的坐标是 .
3.设P和Q是两个集合,定义集合![]() =
=![]() ,如果
,如果![]() ,
,![]() 那么
那么![]() =
=
4.定义在R上的函数f(x)满足关系式:f(![]() +x)+f(
+x)+f(![]() -x)=2,则f(
-x)=2,则f(![]() )+f(
)+f(![]() )+…+f(
)+…+f(![]() )的值等于__________。
)的值等于__________。
5.若向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,则向量
,则向量![]() ,
,![]() 的夹角的大小为
.
的夹角的大小为
.
6.设![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值之差为
上的最大值与最小值之差为![]() ,则
,则![]()
7.若a,b,c均为正实数,且a,b均不为1,则等式![]() 成立的条件是 .
成立的条件是 .
8.教师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质:甲:对于x∈R,都有f(1+x)=f(1-x);乙:在(-∞,0)上,函数递减;丙:在(0,+∞)上函数递增;丁:f(0)不是函数的最小值.
如果其中恰有三人说得正确.请写出一个这样的函数 .
9.函数f (x)=![]() 的单调递增区间为
。
的单调递增区间为
。
10.一元二次方程mx2+(2m-3)x+m-2=0的两根为tanα,tanβ,则tan(α+β)的最小值为______.
11.设![]() ,则使函数
,则使函数![]() 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有![]() 的值为
的值为
12.已知x-3+1=0. 求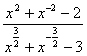 的值
的值
13.已知集合A={x x-a<ax,a>0},若logax>0在A上恒成立,则a的最大值是 .
14.对于函数①![]() ,②
,②![]() ,③
,③![]() .判断如下三个命题的真假:命题甲:
.判断如下三个命题的真假:命题甲:![]() 是偶函数;命题乙:
是偶函数;命题乙:![]() 上是减函数,在区间
上是减函数,在区间![]() 上是增函数;命题丙:
上是增函数;命题丙:![]() 在
在![]() 上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是
上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是
二、解答题
15.已知![]() 为
为![]() 的最小正周期,
的最小正周期,![]() ,且a·b=m.求
,且a·b=m.求![]() 的值.
的值.
16.、已知二次函数f(x) 对任意x∈R,都有f (1-x)=f (1+x)成立,设向量a=(sinx,2), b=(2sinx,![]() ),c=(cos2x,1),d=(1,2)。
),c=(cos2x,1),d=(1,2)。
(1)分别求a·b和c·d的取值范围;
(2)当x∈[0,π]时,求不等式f(a·b)>f(c·d)的解集。
17.某种商品原来定价为每件a元时,每天可售出m件.现在的把定价降低x个百分点(即x%)后,售出数量增加了y个百分点,且每天的销售额是原来的k倍.
(Ⅰ)设y=nx,其中n是大于1的常数,试将k写成x的函数;
(Ⅱ)求销售额最大时x的值(结果可用含n的式子表示);
(Ⅲ)当n=2时,要使销售额比原来有所增加,求x的取值范围.
18.已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() = (2,0)所成角为
= (2,0)所成角为![]() ,其中A、B、C是△ABC的内角.
,其中A、B、C是△ABC的内角.
(Ⅰ)求角B的大小;
(Ⅱ)求sinA + sinC的取值范围.
19.已知a是实数,函数![]() ,如果函数
,如果函数![]() 在区间
在区间![]() 上有零点,求a的取值范围.
上有零点,求a的取值范围.
20.定义在(-1,1)上的函数![]() 满足:①对任意x,
满足:①对任意x,![]() (-1,1)都有
(-1,1)都有![]() ;②当
;②当![]() (-1,0)时,
(-1,0)时,![]() .
.
(Ⅰ)判断![]() 在(-1,1)上的奇偶性,并说明理由;
在(-1,1)上的奇偶性,并说明理由;
(Ⅱ)判断函数![]() 在(0,1)上的单调性,并说明理由;
在(0,1)上的单调性,并说明理由;
(Ⅲ)若![]() ,试求
,试求![]() 的值.
的值.
参考答案
一、选择题
1.1 2.(,0),k∈Z 3. {x0<x≤1}
4. 7 5.![]() 6.4
6.4
7. x=1 8. y=(x-1)2等 9.(6kπ-,6kπ+),k∈Z
10.- 11. 1,3 12. 3
13.: 14. ②
二、解答题
15.解:因为![]() 为
为![]() 的最小正周期,故
的最小正周期,故![]() .
.
因![]() ,又
,又![]() .故
.故![]() .
.
由于![]() ,所以
,所以
![]()
![]()
![]() .
.
16.解:(1)a·b=2sin2x+1![]() 1 c·d=2cos2x+1
1 c·d=2cos2x+1![]() 1
1
(2)∵f(1-x)=f(1+x) ∴f(x)图象关于x=1对称
当二次项系数m>0时, f(x)在(1,![]() )内单调递增,
)内单调递增,
由f(a·b)>f(c·d)![]() a·b > c·d, 即2sin2x+1>2cos2x+1
a·b > c·d, 即2sin2x+1>2cos2x+1
又∵x∈[0,π]
∴x∈![]()
当二次项系数m<0时,f(x)在(1,![]() )内单调递减,
)内单调递减,
由f(a·b)>f(c·d)![]() a·b > c·d, 即2sin2x+1<2cos2x+1
a·b > c·d, 即2sin2x+1<2cos2x+1
又∵x∈[0,π] ∴x∈![]() 、
、
故当m>0时不等式的解集为![]() ;当m<0时不等式的解集为
;当m<0时不等式的解集为![]()
17.解:(Ⅰ)依题意得
a(1-x%)·m(1+y%)=kam,
将y=nx代入,代简得:
k=-![]() +1.
+1.
(Ⅱ)由(Ⅰ)知当x=![]() 时,k值最大,此时销售额=amk,所以此时销售额也最大.
时,k值最大,此时销售额=amk,所以此时销售额也最大.
且销售额最大为![]() 元.
元.
(Ⅲ)当n=2时,k=-![]() x+1,
x+1,
要使销售额有所增加,即k>1.所以
-![]() >0,
>0,
故x∈(0,50)
这就是说,当销售额有所增加时,降价幅度的范围需要在原价的一半以内.
18.解:(Ⅰ)∵ ![]() =(sinB,1-cosB) , 且与向量
=(sinB,1-cosB) , 且与向量![]() =(2,0)所成角为
=(2,0)所成角为![]()
∴ ![]() ,
,
∴ tan =
又∵ 0<B<p Þ 0< < ,
∴ = ,
∴ B = 。
(Ⅱ)由(Ⅰ)可得A + C = ,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当且仅当![]() 。
。
19.解:若![]() ,
, ![]() ,显然在
,显然在![]() 上没有零点, 所以
上没有零点, 所以 ![]() .
.
令 ![]() , 解得
, 解得 ![]()
①当 ![]() 时,
时, ![]() 恰有一个零点在
恰有一个零点在![]() 上;
上;
②当![]() ,即
,即![]() 时,
时,![]() 在
在
![]() 上也恰有一个零点.
上也恰有一个零点.
③当![]() 在
在![]() 上有两个零点时, 则
上有两个零点时, 则
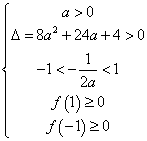 或
或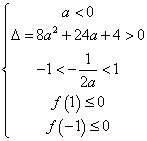
解得![]() 或
或![]()
综上所求实数![]() 的取值范围是
的取值范围是 ![]() 或
或 ![]() .
.
20.(Ⅰ)令![]() .
.
令y=-x,则![]()
![]() 在(-1,1)上是奇函数.
在(-1,1)上是奇函数.
(Ⅱ)设![]() ,则
,则![]() ,
,
而![]() ,
,![]() .
.
![]() .即 当
.即 当![]() 时,
时,![]() .
.
∴ f(x)在(0,1)上单调递减.
(Ⅲ)由于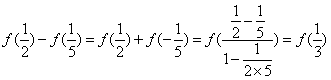 ,
,
![]() ,
,![]() ,
,
∴ ![]() .
.