高一数学上学期期末联考试题
高一数学试卷 2008年1月
命题人：齐齐哈尔第八中学 李庆瑞 齐市实验中学 韩本波
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共120分.考试时间100分钟.
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1、已知
为第四象限角，且
，则
等于
（ ）
A. 
B.
C.
D.
2、已知集合
，则
= （ ）
A.
B.
C.
D.
3、如果
，那么
的值 （ ）
A. 
B.
C.
D.
4、为了得到函数
的图象，只需把函数
的图象上
所有的点 （ ）
A.向左平移
个单位长度 B.向右平移个单位长度
C.向左平移
个单位长度
D.向右平移个单位长度
5、设
，则使函数
的定义域为
，且为奇函数的所有的值为（ ）
A. 1，3
B. ，1
C. -1，3
D. -1，1，3
6、在
中，已知
是
边上一点，若
，且
，
则
=
（ ）
A.
B. 
C.
D.
7、在平行四边形
中，
是平面内的任意一点，且
、
、
、
，则下列运算正确的是
（ ）
A.
B. 
C. 
D.
8、已知
，
，那么
等于
（ ）
A. 
B.
C. 
D.
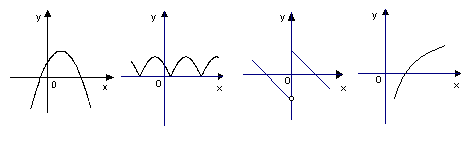
9、下列函数图象与
轴均有交点，其中不能用二分法求图中函数零点的是 （ ）
 |
| |
A. B. C. D.
10、已知定义域为R的函数
在
上为减函数，且函数
为
偶函数，则 （ ）
A.
B.
C.
D.
11、平面内有相异四点、
、
、
满足
，
则的形状是
（ ）
A. 等边三角形 B. 直角三角形
C. 以
为底边的等腰三角形
D. 以为底边的等腰三角形
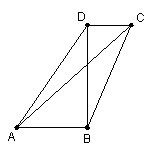12、如图，在四边形ABCD中，
，
则
的值为
（ ）
A.
2 B.
2
C. 4 D. 
第Ⅱ卷（非选择题 共60分）
二、填空题：本大题4小题，每小题4分，共16分. 把正确答案填在题中横线上.
13、已知
、
，则
______________；
14、已知
为实数，函数
在区间
上有零点，
则的取值范围__________________；
15、若
，
且
，则
与
的夹角为______________；
16、若
，则
______________.
三、解答题：本大题共4小题，共44分，解答应写出文字说明，证明过程或演算步骤.
17、（本小题满分10分）
已知顶点的坐标为
（1）
若
，求
的值;
（2）
若为钝角，求
的取值范围.
18、（本小题满分10分）
已知函数
，
.
（1） 函数
是否具有周期性？如果有，请求出最小正周期；如果没有请说明理由；
（2） 设函数
，求函数
单调增区间.
19、（本小题满分12分）
某工厂2007年1，2，3月生产某种产品分别为1万件、1.2万件和1.3万件.为了估
测以后每个月的产量,以这3个月的产品数量为依据,用一个函数模拟该产品的产量
（万件）与月份数的关系，模拟函数可以选用二次函数或函数
（其
中
为常数）.已知4月份该产品的产量为1.37万件.请问用以上哪个函数作为模
拟函数最好？请说明理由.
20、（本小题满分12分）
已知
，
（I）若
，且∥（
），求x的值；
（II）是否存在实数
和，使
？若存在，求出k的取值范围；若不存在，请说明理由.
学期期末联考
高一数学 答题卡 2008年1月
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，
只有一项是符合题目要求的
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在答题卡的横线上.
13、_________________________ 14、_______________________
15、_________________________ 16、_______________________
三、解答题：本大题共4小题，共44分.解答题写出文字说明，证明过程或演算步骤
17、（本题满分10分）
18、（本题满分10分）
19、（本题满分12分）
20、（本题满分12分）
高一数学答案 2008年1月
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | A | D | A | A | B | B | B | D | C | C |
二、填空题： 13、 
14、
15、 16、
三、解答题：本大题共4小题，共44分.解答题写出文字说明，证明过程或演算步骤
17、（本题满分10分）
（1）
……5分
（2）
……10分
18、（本题满分10分）
（1）有周期性
函数最小正周期是
……4分
（2）
……6分
……8分
函数的单调增区间为
……10分
19、（本题满分12分）
设
由
得
……4分
……6分
由
得
……10分
经比较可知，用
作为模拟函数较好
……12分
20、（本题满分12分）
解：（I）
，
∵∥()，
， …………2分
…………5分
（II）
， …………6分
若（
）⊥（），则（）·（）=0，
即
，
， …………9分
x∈R，
存在
…………12分