高一数学下册3月月考试卷
一.选择题：（每小题5分，共60分）
1．下列给出的赋值语句中正确的是（ ）
A．
B．
C．
D．
2．某企业有职工
人，其中高级职称
人，中级职称
人，一般职员
人，现抽取
人进行分层抽样，则各职称
人数分别为（ ）
A．
B．
C．
D．
3．右边程序执行后输出的结果是（ ）
A．
B．
C．1 D．2
4．样本4，2，1，0，－2的标准差是：
A．1 B．2
C．4
D．
5．从三件正品、一件次品中随机取出两件，则取出的产品全是正品的概率是（ ）
A．
B．
C．
D．无法确定
6．用秦九韶算法求多项式
在
的值时，其中
的值为（ ）．
A．-57 B．124 C．-845 D．220
7．有五条线段长度分别为
，从这
条线段中任取
条，
则所取条线段能构成一个三角形的概率为（
）
A．
B．
C．
D．
8．从装有
个红球和个黒球的口袋内任取个球，那么互斥而不对立的两个事件是（ ）
A．至少有一个黒球与都是黒球 B．至少有一个黒球与都是黒球
C．至少有一个黒球与至少有
个红球 D．恰有个黒球与恰有个黒球
9．在
根纤维中，有
根的长度超过
，从中任取一根，取到长度超过的纤维的概率是（ ）
A．
B．
C．
D．以上都不对
10．数4557，1953，5115的最大公约数为（ ）．
A．93 B．31 C．651 D．217
11．设有一个直线回归方程为 
,则变量x 增加一个单位时 ( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位
12．某次考试有70000名学生参加，为了了解这70000名考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，在这个问题中，有以下四种说法：
（1） 1000名考生是总体的一个样本；
（2） 1000名考生数学成绩的平均数是总体平均数；
（3） 70000名考生是总体；
（4） 样本容量是1000，
其中正确的说法有：
A．1种 B．2种 C．3种 D．4种
二.填空题：（每小题4分，共16分）
13. 一个容量为20的样本数据,分组后,组距与频数如下: 
,2; 
, 3 ; 
, 4 ; 
, 5 ; 
, 4 ; 
, 2 .则样本在区间
上的频率为_______________．
14. 有一个简单的随机样本: 10, 12, 9, 14,
13 则样本平均数
=______ ,样本方差
=__________．
15．在编号为1，2，3，…，n的n张奖卷中，采取不放回方式抽奖，若1号为获奖号码，则在第k次（1≤k≤n）抽签时抽到1号奖卷的概率为________。
16. 下列各数
、
、 
、 
中最小的数是_________．
龙岩高级中学
高一数学月考答题卷 2008.3.29
| 一 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
二.填空题
13. _____________ 14.______________ 15.______________ 16._____________
三.解答题：
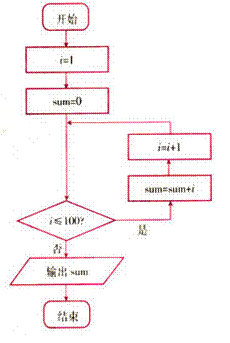
17.以下是计算
程序框图,请写出对应的程序.（12分）
18. （12分） 如图，在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是多少？
19.（12分）对甲、乙的学习成绩进行抽样分析，各抽门功课，得到的观测值如下：
问：甲、乙谁的平均成绩最好？谁的各门功课发展较平衡？
20.（12分） 函数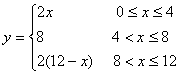
，写出求函数的函数值的程序.
21.（12分）袋中有大小相同的红、黄两种颜色的球各个，从中任取只，有放回地抽取次． 求：
① 只全是红球的概率；
② 只颜色全相同的概率；
③ 只颜色不全相同的概率.
22.（14分）
以下是某地搜集到的新房屋的销售价格
和房屋的面积
的数据：
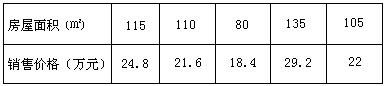
（1）画出数据对应的散点图；
（2）求线性回归方程，并在散点图中加上回归直线；
（3）据（2）的结果估计当房屋面积为
时的销售价格.
龙岩高级中学高一数学月考答案
一.选择题1．B 2.B 3B 4.B 5.B 6.D 7.B 8.D 9.B 10.A 11.C 12.A
二.填空题：13.[0，3] 14。[11.6，3.44] 15.[1/n] 16.111111（2）
17. 解： i=1
sum=0
WHILE i<=100
sum=sum+i
i=i+1
WEND
PRINT sum
END
18解：INPUT “x=”;x
IF x>=0 and x<=4 THEN
y=2
x
ELSE IF x<=8 THEN
y=8
ELSE y=2*(12-x)
END IF
END IF
PRINT y
END
19解：
∵ 
∴ 甲的平均成绩较好，乙的各门功课发展较平衡
20.略
21解：①每次抽到红球的概率为
②每次抽到红球或黄球
③颜色不全相同是全相同的对立，
22.解：（1）数据对应的散点图如图所示：
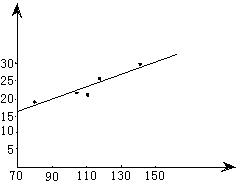
（2）
，
，
设所求回归直线方程为
，
则
故所求回归直线方程为
（3）据（2），当
时，销售价格的估计值为：
（万元）