姓名_______
学号________ 高一第一学期集合与函数单元测试试题（3）
班级_________
撰稿： 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题（每小题5分，共50分）(填空题的答案请全部填写在第10题后的表格之中)
★1、设
是
上的任意函数，下列叙述正确的是（ ）
A、
是奇函数；
B、
是奇函数；
C、
是偶函数；
D、
是偶函数
★2、下列各式错误的是（ ）.
A. 
B. 
C. 
D. 
★3、设集合
,
，若M∩N=Æ，则
的取值范围是（ ）
A．
B．
C．
D．[－1，2]
★4、 已知
，且
则
的值为（ ）.
A. 4
B. 0
C. 2m D. 
★5、 函数
的单调递减区间为（ ）.
A. 
B. 
C. 
D. 
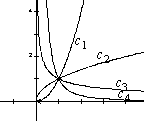★6、
如图的曲线是幂函数
在第一象限内的图象. 已知
分别取
，
四个值，与曲线
、
、
、
相应的依次为（ ）.
A．
B. 
C. 
D. 
★
7、 定义集合A、B的一种运算：
，若
，
，则
中的所有元素数字之和为（ ）.
A．9 B. 14 C.18 D.21
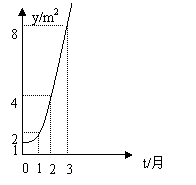
★8、 如图所示的是某池塘中的浮萍蔓延的面积(
)与时间
(月)
的关系:
,有以下叙述：
① 这个指数函数的底数是2; ② 第5个月时,浮萍的面积就会超过
； ③ 浮萍从
蔓延到
需要经过1.5个月; ④ 浮萍每个月增加的面积都相等；其中正确的是（ ）.
A. ①②③ B. ①②③④ C. ②③④ D. ①②
★题9、在
上定义的函数
是偶函数，且
，若在区间
是减函数，则函数（ ）
A.在区间
上是增函数，区间
上是增函数；
B.在区间上是增函数，区间上是减函数；
C.在区间上是减函数，区间上是增函数；
D.在区间上是减函数，区间上是减函数
★10、函数y=f(x)与y=g(x)的图象如所示：
则函数y=f(x)·g(x)的图象可能为( )
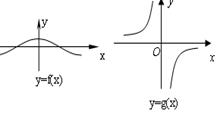
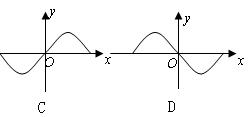
请将选择题答案的答案下在下面：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二、填空题（每小题5分，共25分）
★11、设函数
为奇函数，则实数
。
★12.、函数
的定义域为 . （用区间表示）
★13.、
；若
.
★14、我国的人口约13亿，如果今后能将人口数年平均增长率控制在1%，那么经过x年后我国人口数为y亿，则y与x的关系式为____________________.
★15、对于函数
,定义域为D, 若存在
使
, 则称
为的图象上的不动点. 由此，函数
的图象上不动点的坐标为
.
三、解答题
★16题（10分）、. 已知集合A=｛xx2-3x-10≤0｝,B=｛xm+1≤x≤2m-1｝,若A∪B=A，求出实数m的取值范围。
★17题（13分）、某租赁公司拥有汽车100辆，当每辆月租金3000元时，可全部租出，当每辆车的月租金增加50元时，末租出的车将会增加一辆，租出的车每辆每月需要维护费150元，末租出的车每辆每月需要保管费50元。问：（1）、当每辆车的月租金定为3600元时，能租出去多少辆车？（2）、每辆车的月租金定为多少元时，租赁公司的月收益最大？最大的月收益可达多少？
★18题（13分）、定义在
上的函数f(x)，对于任意的
，都有
成立，当
时，
. （Ⅰ）计算
； （Ⅱ）证明f (x)在上是减函数； （Ⅲ）当
时，解不等式
.
★19（13分）、已知0<a<1,在函数y= logax (x≥1)的图象上有A、B、C三点，它们的横坐标分别是t、t+2、t+4；
①、记△ABC的面积为S，求出S=f(t)的表达式；并判断出S== f(t)的单调性；
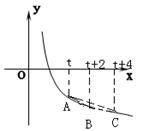②、求出S=f(t)的最大值。
★20（13分）. 光线通过一块玻璃,其强度要损失
,把几块这样的玻璃重叠起来,设光线原来的强度为
,通过
块玻璃后强度为
. （1）写出关于的函数关系式；
（2）通过多少块玻璃后，光线强度减弱到原来的
以下? ( 
★21（13分）. 已知函数
.
（1）求证：不论为何实数总是为增函数；（2）确定的值, 使为奇函数；（3）当为奇函数时, 求的值域.
高一第一学期《集合与函数》单元测试试题（3）参考答案
一、选择题答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | C | B | A | D | A | B | D | B | A |
二、填空题和解答题：
★11、-1； ★12.、
；
★13.、
0 ；若 4 .
★14、
；
★15、
.
★16题、解：（见教案P63面题1）m≤3
★17题、 ●解:(1)100-12=88;(2)、y=x2+162x-21000= (x-4050)2+307050(3000≤x<8000),则当x=4050时，最大收益为307050元。
★18题、●解:（Ⅰ）
. （II）设
, 因为
即
,所以
.因为，则
，而当时，, 从而
于是
在上是减函数. （Ⅲ）因为
, 所以
,
因为在上是减函数，所以
,
解得 
或
, 故所求不等式的解集为
或
.
★19. 解；①、S= f(t) = loga [] = loga [1- ]；为↘；②、当t=1时，S= f(t)最大值为loga 。
★20. 解析: (1) 
(2) 
∴ 
.
★21. 解析: (1) 
的定义域为R, 设
,则
=
,
, 
,
即
,所以不论为何实数总为增函数.
(2) 为奇函数, 
,即
,
解得: 
（3） 由(2)知
, 
,
,
所以的值域为