学号__________姓名_____ 高一第二学期必修三与必修四综合测试(1)
撰稿: 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一:选择题:
1. 已知向量![]() =(4,2),向量
=(4,2),向量![]() =(
=(![]() ,3),且
,3),且![]() //
//![]() , 则
, 则![]() 等于( )
等于( )
A. 9 B. 6 C. 5 D. 3
2. tan600°的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 3. 某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家. 为了掌握各商店的营业情况,要从中抽取一个容量为20的样本. 若采用分层抽样的方法,抽取的中型商店数是( )
3. 某地区有300家商店,其中大型商店有30家,中型商店有75家,小型商店有195家. 为了掌握各商店的营业情况,要从中抽取一个容量为20的样本. 若采用分层抽样的方法,抽取的中型商店数是( )
A. 2 B. 3 C. 5 D. 13
4. 下列各数中最小的数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
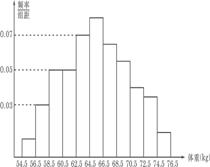
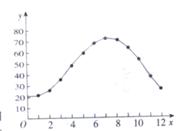
5. 为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( ) A. 20 B. 30 C. 40 D. 50
6. 已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 则
则![]() 等于( )
等于( )
A. 5 B. 4 C. 3 D. 1
 7. 若△
7. 若△![]() 的内角
的内角![]() 满足
满足![]() ,则
,则![]() =( )
=( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
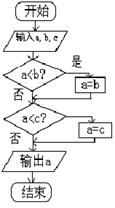
8. 右图给出一个算法的程序框图,该程序框图的功能是( )
A.求输出a,b,c三数的最大数 B.求输出a,b,c三数的最小数
C.将a,b,c按从小到大排列 D.将a,b,c按从大到小排列
9. 已知![]() 则
则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 将函数![]() 的图象沿x轴方向左平移
的图象沿x轴方向左平移![]() 个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( )
个单位,平移后的图象如右图所示. 则平移后的图象所对应函数的解析式是( )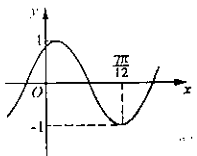 A.
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
11. ![]() 的值为
.
的值为
.
12. 已知向量![]() ,
,![]() ,则
,则![]() 的最大值为 .
的最大值为 .
13. 某班委会由4名男生与3名女生组成,现从中选出2人担任正副班长,其中至少有1名女生当选的概率是 . (用分数作答)
14. 规定运算![]() ,若
,若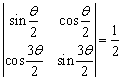 ,则
,则![]() = .
= .
15、一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ .
三、解答题
16. 已知![]() ,
,![]() ,
,
(1)求![]() 与
与![]() 的夹角
的夹角![]() ; (2)若
; (2)若![]() ,且
,且![]() ,试求
,试求![]() .
.
17. (一)小题:
甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为![]() 和
和![]() , 求:
, 求:
(1)甲、乙两人至少有一个人破译出密码的概率; (2)两人都没有破译出密码的概率.
(二)小题:玻璃球盒中装有各色球12只,其中5红、4黑、2白、1绿.
(1)从中取1个球, 求取得红或黑的概率;(2)从中取2个球,求至少一个红球的概率.
(三)小题:若以连续掷两次骰子分别得到的点数m、n作为点P的坐标![]() ,则点P在圆
,则点P在圆![]() 外的概率是多少?
外的概率是多少?
18(一)小题:. 对任意正整数![]() ,设计一个求S=
,设计一个求S=![]() 的程序框图,并编写出程序.
的程序框图,并编写出程序.
(二)小题:假设关于某种设备的使用年限![]() 和支出的维修费用
和支出的维修费用![]() (万元),有以下的统计资料:
(万元),有以下的统计资料:
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图; (2)求支出的维修费用![]() 与使用年限
与使用年限![]() 的回归方程;
的回归方程;
(3)估计使用年限为10年时,维修费用是多少?
19. 已知函数![]() . (1)用五点法画出它在一个周期内的闭区间上的图象;
. (1)用五点法画出它在一个周期内的闭区间上的图象;
(2)说明此函数图象可由![]() 上的图象经怎样的变换得到;(3)由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.
上的图象经怎样的变换得到;(3)由图象指出函数的单调递减区间、对称轴方程和对称中心点坐标.
20.设向量![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosx,cosx),x∈R,函数f(x)=
=(cosx,cosx),x∈R,函数f(x)=![]() .
.
(1)求函数f(x)的最大值与最小正周期;(2)求使不等式f(x)≥![]() 成立的x的取值集合.
成立的x的取值集合.
21. 下表是芝加哥1951~1981年月平均气温(华氏):
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均气温 | 21.0 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 | 73.0 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
(1) 以月份为x轴,x=月份-1,以平均气温为y轴,描出散点图,并用一个函数模型近似地描述y与x之间的函数关系.(2)某蔬菜的种植,要求每月的平均气温不低于60华氏,试确定蔬菜在一年内种植的最长时间.
学号__________姓名________ 高一第二学期·必修三与必修四综合测试题(2)
撰稿: 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一:选择题:
1. ![]() 的值是( )
的值是( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2 一个单位有职工160人,其中有业务员104人,管理人员32人,后勤服务人员24人,要从中抽取一个容量为20的样本,用分层抽样的方法抽取样本,则在20人的样本中应抽取管理人员人数为 ( )
A. 3 B. 4 C. 5 D. 6
3. 某人一次掷出两枚骰子,点数和为5的概率是( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
4.有一个数据为50的样本,其分组以及各组的频数如下:
[12.5,15.5],3;
[15.5,18.5],8; [18.5,21.5],9; [21.5,24.5],11; [24.4,27.5],10; [27.5,30.5],5;
[30.5,33.5],4 由以上频数,估计不超过![]() 的数据大约占( )
的数据大约占( )
A.10% B.92% C.5% D.30%
5. 某产品分甲、乙、丙三级,其中乙、丙两级均属次品.若生产中出现乙级品的概率为0.03,丙级品的概率为0.01,则对成品抽查一件抽得正品的概率为( )
A.0.99 B.0.98 C.0.97 D.0.96
 6. 已知α为第二象限角,那么
6. 已知α为第二象限角,那么![]() 是( )
是( )
A.第一象限角 B. 第二象限角 C.第一、三象限角 D.第二、四象限
7. 将十进制数111化为五进制数是( )
A.421(5) B. 521(5) C.423(5) D. 332(5)
8. 下面为一个求10个数的平均数的程序,在横线上应填充的语句为
A. i>10 B.i<10 C. i>=10 D i<=10
9. 一个游戏转盘上有四种颜色:红、黄、蓝、黑,并且它们所占面积的比为6:2:1:4,则指针停在红色或蓝色区域的概率为( )
A.B.
C.
D.
10、将函数y=sin(3x+![]() )的图像向右平移
)的图像向右平移![]() 个单位,得到函数y=sin3x的图像,则
个单位,得到函数y=sin3x的图像,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
11. 甲、乙两名高一男生参加投篮测试,各投篮5次,一分钟内投中次数分别如下:
甲:7,8,6,8,6; 乙:7,8,7,7,6
甲的方差是_______ ,乙的方差是________ ,说明 ______ 投篮更稳定.
 12. 一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ .
12. 一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒,当你到达路口时,看见绿灯的概率是__________ .
13.终边落在阴影部分处(包括边界)的角的集合是_________(用弧度制表示)
14.已知![]() ,则
,则![]() ____________.
____________.
15、关于下列各命题:
①函数![]() 在第一象限是增函数; ②函数
在第一象限是增函数; ②函数![]() 是非奇非偶函数;
是非奇非偶函数;
③函数![]() 的一条对称轴是
的一条对称轴是![]() ; ④函数
; ④函数![]() 是实数集上的偶函数
是实数集上的偶函数
其中正确命题的序号是 。
三、解答题
16.玻璃球盒中装有各色球12只,其中5红、4黑、2白、1绿.
(1)从中取1个球, 求取得红或黑的概率; (2)从中取2个球,求至少一个红球的概率.
17、已知![]() ,
,![]() 为原点。
为原点。
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的夹角。
的夹角。
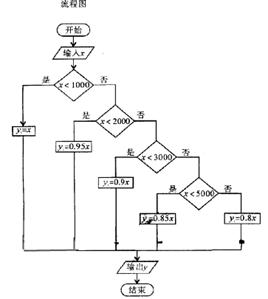
18、某商场为了促销,采用购物打折的优惠办法: 每位顾客一次购物:
①在1000元及以上且2000元以下者按九五折优惠; ②在2000元以上且3000元以下者按九折优惠; ③在3000元以上且5000元以下者按八五折优惠; ④在5000元及以上者按八折优惠.
求:(1)写出函数关系式;
(2)试编写流程图求优惠价,写出相应的程序
19、在数学考试中,小丽的成绩在90分以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09.计算小丽在数学考试中取得80分以上成绩的概率和小丽考试及格的概率.
20、平面直角坐标系中,![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() 为直角顶点。
为直角顶点。
(Ⅰ)求点![]() ;
;
(Ⅱ)设点![]() 是第一象限的点,若
是第一象限的点,若![]() ,
,![]() ,则
,则![]() 为何值时,点
为何值时,点![]() 在第二象限?
在第二象限?
21. 已知向量![]() ,且
,且![]() ,求:
,求:
(1)![]() 及
及![]() ;
;
(2)若![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值。
的值。
综合(一)参考答案:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | D | C | B | A | A | A | C |
11.-![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ; 14.
; 14. ![]() ; 15、8/15
; 15、8/15
16. 解:(1)∵![]() =61,
=61,
∴ ![]() =
=![]() , ∴
, ∴ ![]() . (2)设
. (2)设![]() ,则
,则
![]() ,解得
,解得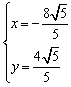 或
或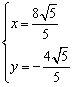 . 所以,
. 所以,![]() 或
或![]() .
.
17. (一)小题解:解(1)设甲破译密码的事件为A, 乙破译密码的事件为B, 则 P(A+B)=P(A)+P(B)= + = 答: 至少有一个人破译出密码的概率为 (2)设两人都没有破译的事件为C, 则P(C)=1-P(A+B)=1- = 答: 两人都没有破译出密码的概率为
(二)小题解:(1)从12只球中任取1球得红球有5种取法,得黑球有4种取法,得红球或黑球的共有5+4=9种不同取法,任取一球有12种取法,所以任取1球得红球或黑球的概率得![]()
(2)从12只球中任取2球至少一个红球有2类取法,得1个红球有5×7种方法,得两个红球有![]() 种取法,从所求概率为
种取法,从所求概率为 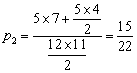
18题:(二)、(1) ![]() a=0.08 b=1.23; (2)维修费用=12.38
a=0.08 b=1.23; (2)维修费用=12.38
19. 解:(1)![]() . 最小正周期
. 最小正周期 ![]() ; (3)单调递减区间为
; (3)单调递减区间为![]() ;对称轴方程为
;对称轴方程为![]() ;对称中心点坐标为
;对称中心点坐标为![]() .
.
20. 解:(1)![]()
![]() ∴
∴![]() 的最大值为
的最大值为![]() ,最小正周期是
,最小正周期是![]() . (2)由(1)知
. (2)由(1)知 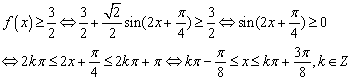
 即
即![]() 成立的
成立的![]() 的取值集合是
的取值集合是![]() .
.
21、 解:(1)作出的散点图如图所示. 根据图形,可选择正弦曲线![]() 进行拟合.
进行拟合.
易知,![]() ,T=12,
,T=12,![]() . 则
. 则![]() ,
,![]() 把x=0代入,得
把x=0代入,得![]() ,即
,即![]() .所以,拟合的函数模型为
.所以,拟合的函数模型为![]() .(2)由
.(2)由![]() ,即
,即![]() ,解得
,解得![]() .所以,该蔬菜在一年内种植的最长时间为5个月.
.所以,该蔬菜在一年内种植的最长时间为5个月.
综合(二)参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | B | B | D | C | A | A | B | A |
11、 0.8; 0.4; 乙; 12.![]() ;13.
;13. ![]() ; 14.
; 14.
![]() 15、④
15、④
16解:(1)从12只球中任取1球得红球有5种取法,得黑球有4种取法,得红球或黑球的共有5+4=9种不同取法,任取一球有12种取法,所以任取1球得红球或黑球的概率得![]()
(2)从12只球中任取2球至少一个红球有2类取法,得1个红球有5×7种方法,得两个红球有![]() 种取法,从所求概率为
种取法,从所求概率为 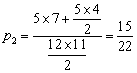
17.解:(Ⅰ)![]()
![]() (Ⅱ)
(Ⅱ)![]()
![]() ,
,![]() ;又
;又![]() ,
,![]()
![]() ,
,![]() 设
设![]() 的夹角为
的夹角为![]() ,则
,则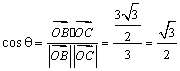 . 又
. 又![]()
18.解: 设购物款数原为x元, 优惠后人格为y元, 则优惠付款方式可用分段函数表示为
19、解:分别记小丽的考试成绩在90分以上、在80~89分、在70~79分、在60~69分分别为事件B、C、D、E,这4个事件是彼此互斥的,根据互斥事件的概率加法公式,小丽的考试成绩在80分以上的概率是P(B∪C)=P(B)+P(C)=0.18+0.51=0.69.
小丽考试及格的概率,即成绩在60分以上的概率,由公式得P(B∪C∪D∪E)=P(B)+P(C)+P(D)+P(E)=0.18+0.51+0.15+0.09=0.93.
20.解:(Ⅰ)由已知 ![]() ,
,![]() ,
, ![]() ,
,![]()
![]()
即![]()
![]() 又
又![]() ,即
,即![]() ,
,
即![]() 将
将![]() 代入
代入![]() 消去
消去![]() 得
得 ![]()
解得![]() 或
或![]() ,相应的
,相应的![]() 或
或![]() 所以点
所以点![]() 为
为 ![]() 或
或![]()
(Ⅱ)由题意取![]() ,
, ![]() ,
,![]()
![]() ,
, ![]()
![]() 若点
若点![]() 在第二象限,则
在第二象限,则![]() ,解得
,解得![]() 所以,当
所以,当![]() 时,点
时,点![]() 在第二象限。
在第二象限。
21.解:(1)![]()
![]()
![]()
又![]() 从而
从而![]()
(2)![]()
![]()
 由于
由于![]() 故
故![]() ①当
①当![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,这与题设矛盾;②当
,这与题设矛盾;②当![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,由
,由![]() 及
及![]() 得
得![]() ;③当
;③当![]() 时,当且仅当
时,当且仅当![]() 时,
时,![]() 取得最小值
取得最小值![]() ,由
,由![]() ,得
,得![]() 与
与![]() 矛盾综上所述,
矛盾综上所述,![]() 即为所求。
即为所求。