_____班;姓名______学号______ 高一第二学期必修三与必修四综合测试题(3)
撰稿: 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一:选择题:
 1. 化简
1. 化简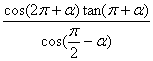 为 ( ):
为 ( ): ![]()
![]()
![]()
![]()
2.![]() 的值为( ) A.2 B.
4 C.-4 D.不存在
的值为( ) A.2 B.
4 C.-4 D.不存在
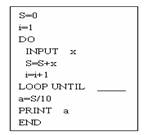
3. 下面为一个求10个数的平均数的程序,在横线上应填充的语句为( )
A. i>10 B.i<10 C. i>=10 D i<=10
4.从一批螺母产品中任取一个,测量其横截面直径的大小,直径小于3.98![]() 的概率为0.38,直径小于4.06
的概率为0.38,直径小于4.06![]() 的概率为0.30,那么直径在[3.98,4.06)范围内的概率是( )
的概率为0.30,那么直径在[3.98,4.06)范围内的概率是( )
A. 0.68 B. 0.38 C. 0.08 D. 0.62
5.现有五个球分别记为1,2,3,4,5,随机取出三个球放进三个盒子,每个盒子放一个球,则1或2在盒中的概率是( )
A. 1/10 B. 3/5 C.3/10 D. 9/10
6.已知![]() 中,
中,![]() 为
为![]() 边上的中点, 则下列等式中正确的是( )
边上的中点, 则下列等式中正确的是( )
![]()
![]()
![]()
![]()
7. 要得到函数![]() 的图象,只须将函数
的图象,只须将函数![]() 的图象( ) (A)向右平移
的图象( ) (A)向右平移![]() 个单位 (B)向左平移
个单位 (B)向左平移![]() 个单位 (C)横坐标伸长到原来的2倍 (D)横坐标缩短到原来的1/2倍
个单位 (C)横坐标伸长到原来的2倍 (D)横坐标缩短到原来的1/2倍
8.设![]() ,若
,若![]() 的夹角为
的夹角为![]() ,
,![]() 的夹角为
的夹角为![]() ,且
,且![]() ,则
,则![]() 的值为( ) A.
的值为( ) A.![]() B.
B.![]() C.1/2 D.1
C.1/2 D.1
9.函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() =(
)
=(
)
A.16
B. ![]() C.8
D.
C.8
D.![]()
10.已知平行四边形![]() 的3个顶点为
的3个顶点为![]() ,则它的第4个顶点
,则它的第4个顶点![]() 的坐标是( )
的坐标是( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题:
11. 一个总体中共有200个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被抽到的可能性是
12.当![]()
![]() 时,则
时,则![]() 的概率为 .
的概率为 .
13.若![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() ,则
,则![]() =
=
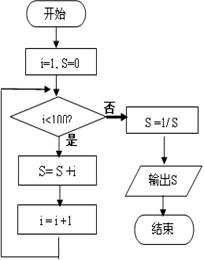
14、图中所示的是一个算法的流程图,其表达式为
15、掷两颗骰子,出现点数之和等于8的概率等于__________.
三.解答题:
16题. 已知函数![]() .
.
(1)求函数的最大值、最小值及取得最大值和最小值时自变量![]() 的集合.
的集合.
(2) 求函数的单调递增区间.
17题.已知![]() ;(1) 若
;(1) 若![]() 两向量所成角
两向量所成角![]() , 求
, 求![]() .
.
(2) 若![]() 两向量所成的角
两向量所成的角![]() ,求
,求![]() 的大小.
的大小.
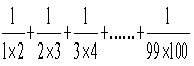 18题、(1)、甲乙两人约定在下午6点到7点之间于某地会面,先到者等候时间不超过一刻钟,过时即可离去,求两人能会面的概率。
18题、(1)、甲乙两人约定在下午6点到7点之间于某地会面,先到者等候时间不超过一刻钟,过时即可离去,求两人能会面的概率。
(2)、设计算法求值,要求画出程序框图,写出用基本语句编写的程序。
19题、现有一批产品共有![]() 件,其中
件,其中![]() 件为正品,
件为正品,![]() 件为次品: (1)如果从中取出一件,然后放回,再取一件,求连续
件为次品: (1)如果从中取出一件,然后放回,再取一件,求连续![]() 次取出的都是正品的概率; (2)如果从中一次取
次取出的都是正品的概率; (2)如果从中一次取![]() 件,求
件,求![]() 件都是正品的概率
件都是正品的概率
20、已知![]() ,
,![]() ,其中
,其中![]()
![]() (1)求证:
(1)求证:![]() 与
与![]() 互相垂直; (2)若
互相垂直; (2)若![]()
![]() 与
与![]()
![]() 的长度相等,求
的长度相等,求![]() 的值(
的值(![]() 为非零的常数)
为非零的常数)![]()
21、已知![]() 的面积
的面积![]() 满足
满足![]() ,且
,且![]() ;
;
(1)求函数![]() 的最大值;
的最大值;
(2)若 ![]() ,求
,求![]() 的取值范围。
的取值范围。
高一第二学期·必修三与必修四综合测试题(4)
一:选择题:
1、函数![]() 是( ) A.最小正周期为
是( ) A.最小正周期为![]() 的偶函数; B.最小正周期为
的偶函数; B.最小正周期为![]() 的偶函数; C.最小正周期为
的偶函数; C.最小正周期为![]() 的奇函数; D.最小正周期为
的奇函数; D.最小正周期为![]() 的奇函数;
的奇函数;
2、设P为△ABC所在平面内一点,且满足![]() ,则P是△ABC的( )
,则P是△ABC的( )
A.重心; B.垂心; C.外心; D.内心;
3、已知![]() 与
与![]() 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为![]() ,那么
,那么![]() = ( )
= ( )
A.![]() ;
B.1;
C.
;
B.1;
C.![]() ;
D.4;
;
D.4;
4、函数![]() 在[0,
在[0,![]() ]的值域是 ( )
]的值域是 ( )
A.[―1,1]; B.[1/2,1] C.[0,1] D.[-1/2―,1]
5、![]() ,若
,若![]() ,则
,则![]() 夹角为( ) A、
夹角为( ) A、![]() /2 ; B、
/2 ; B、![]() /4; C、
/4; C、![]() /3; D、
/3; D、![]() /6;
/6;
6、某个路口的交通指示灯,红灯时间为30秒,黄灯时间为10秒,绿灯时间为40秒.当你到达路口时,看见红灯的概率是( )A.1/2 ; B.1/8 ; C.3/8 ; D.5/8;
7、射击场上的箭靶半径为90厘米,靶心半径为20厘米,则射中靶心的慨率为 ( )
A、2/9; B、 2/7; C、4/49; D、4/81 ;
8、设函数![]() (其中
(其中![]() ),若函数
),若函数![]() 图象的一条
图象的一条
对称轴为![]() ,那么
,那么![]() ( )A.1/2;
B.1/3; C.1/4 ; D.1/6 ;
( )A.1/2;
B.1/3; C.1/4 ; D.1/6 ;
9、已知点![]() 、
、![]() ,点P在线段AB上,且
,点P在线段AB上,且![]() ,则点P的坐标是( )
,则点P的坐标是( )
A.(5/3,1); B.(8/3,1); C.(―8/3,1); D.(―5/3,―1);
10、某班共有6个数学研究性学习小组,本学期初有其它班的3名同学准备加入到这6个小组中去,则这3名同学恰好有2人安排在同一个小组的概率是( )A. 5/12; B.5/24 ; C. 10/81; D.1/5
二、填空题:
11、从分别写有1,2,3,4,5,6的六张卡片中任取两张,这两张卡片上的数字之和为偶数的概率是____ ;
12、已知:![]() =2,
=2,![]() =
=![]() ,
,![]() 与
与![]() 的夹角为45°,要使
的夹角为45°,要使![]() 与
与![]() 垂直,则
垂直,则![]() ______
______
13、若向量![]() =(3,4)围绕原点按逆时针方向旋转
=(3,4)围绕原点按逆时针方向旋转![]() 得到向量
得到向量![]() ,则
,则![]() 的坐标是 .
的坐标是 .
14、向量![]() 与向量
与向量![]() 的夹角为60°,且有
的夹角为60°,且有![]() ,则
,则![]() 的值为_______
的值为_______
15、(1)△ABC中,![]() ,
,![]() ,则
,则![]() ______;(2)把89化为二进制数为______
______;(2)把89化为二进制数为______
16、(1)、函数![]() 的单调递增区间是 ________(2)用辗转相除法求得225和135的最大公约数是______
(3) 用秦九韶算法求多项式
的单调递增区间是 ________(2)用辗转相除法求得225和135的最大公约数是______
(3) 用秦九韶算法求多项式![]() 在x=5时之值,要进行___次乘法运算和__次加法运算.
三、解答题:
在x=5时之值,要进行___次乘法运算和__次加法运算.
三、解答题:
17、设![]() (―1,―2),
(―1,―2),![]() (3,2),且
(3,2),且![]() 在
在![]() 的延长线上,使
的延长线上,使![]() =3
=3![]() ,则求点
,则求点![]() 的坐标;
的坐标;
18、甲、乙两名篮球运动员,甲投篮命中的概率为0.8,乙投篮命中的概率为0.9,两人是否投中相互之间没有影响。 (Ⅰ)两人各投一次,求只有一人命中的概率;(保留两位有效数字);
(Ⅱ)两人各投两次,甲投中两次且乙投中一次的概率。(保留三位有效数字);
19、已知![]() ,(Ⅰ)求
,(Ⅰ)求![]() 的值;(Ⅱ)求
的值;(Ⅱ)求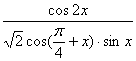 的值.
的值.
20、甲箱的产品中有6个正品和3个次品, 乙箱的产品中有5个正品和3个次品.
(Ⅰ)从甲箱中任取2个产品,求这2个产品都是次品的概率;(用分数表示); (Ⅱ)若从甲箱中任取2个产品放入乙箱中, 然后再从乙箱中任取一个产品,求取出的这个产品是正品的概率.(用分数表示)
21、已知点A(1,0),M(1+cos2x,1),N (2,![]() sin2x+2m),
sin2x+2m),![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 。 (1)求
。 (1)求![]() 的解析式; (2)若xÎ[0,
的解析式; (2)若xÎ[0, ![]() ], 且
], 且![]() 的最小值为6,求
的最小值为6,求![]() 的值。
的值。
22、已知函数f(x)=2 a sin2x+2 sinx cosx-a ,( a为常数) 的图象过点 ( 0, - ) ,(1)求函数f(x)的值域; (2)若将函数y=f(x)的图象向右平移1/2m个单位后(作长度最短的平移),其图象关于y轴对称,求出m的值.
高一第二学期·必修三与必修四综合测试题(5)
一、选择题:
1、现有 ![]() 辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,时速在
辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,时速在![]() 的汽车大约有( )
的汽车大约有( )![]() .
.![]() 辆
辆
![]() .
.![]() 辆
辆 ![]() .
.![]() 辆
辆 ![]() .80辆
.80辆
2、若sin2α<0,且tanα·cosα<0,则角α在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、已知函数![]() 则它是( )函数:A.偶 B.奇 C.非奇非偶 D.不确定
则它是( )函数:A.偶 B.奇 C.非奇非偶 D.不确定
4、在120个零件中,一级品24个,二级品36个,三级品60个。用系统抽样法从中抽取容量为20的样本.则每个个体被抽取到的概率是 ( )A.1/6 B.1/24 C.1/36 D.1/60
5、已知a与b均为单位向量,它们的夹角为60°,那么![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D. 4
D. 4
6、若角![]() 满足sin
满足sin![]()
![]() +cos
+cos![]()
![]() =―sin
=―sin![]() ―cos
―cos![]() ,则
,则![]() 为 ( )
为 ( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限
7、已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,若向量
,若向量![]() ,且
,且![]() ⊥
⊥![]() ,则
,则![]() =( )
=( )
A.2 B.![]() C.1/2 D.
C.1/2 D.![]()
8、已知向量![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的夹角为( )
的夹角为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、把函数y=cos(x+![]() )的图象向右平移φ个单位,所得的图象正好关于y轴对称,则φ的最小正值为(
)
)的图象向右平移φ个单位,所得的图象正好关于y轴对称,则φ的最小正值为(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10、已知A、B、C三点不共线,O是△ABC内的一点,若![]() +
+![]() +
+![]() =0,则O是△ABC的( )
=0,则O是△ABC的( )
A、内心 B、外心 C、垂心 D、重心
二、填空题:
11、用秦九韶算法求多项式![]() 在x=-4时,
在x=-4时,![]() 之值为______
之值为______
12、(1)、已知![]() ,则
,则![]() 的值是 ;(2)、二进制数101101化为八进制数为____
的值是 ;(2)、二进制数101101化为八进制数为____
13、在△ABC中,若a=2, b=2![]() , c=
, c=![]() +
+![]() ,则∠A的度数是
,
,则∠A的度数是
,
14、函数![]() 的图象的对称轴方程是
的图象的对称轴方程是
15、(1)、![]() =_____;(2)用辗转相除法求得153、119的最大公约数是_____
=_____;(2)用辗转相除法求得153、119的最大公约数是_____
16、函数![]() 的单调递减区间是
;
的单调递减区间是
;
三、解答题
17、已知函数![]() ,
,
①、求其最小正周期; ②、求其最大值; ③、求其单调增区间;
18、把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,向量![]() =(―1,-2),①、若向量
=(―1,-2),①、若向量![]() =(―a,b),求当
=(―a,b),求当 ![]() ⊥
⊥![]() 时的慨率;②、若向量
时的慨率;②、若向量![]() =(a,b),又
=(a,b),又![]() ∥
∥![]() , 且
, 且![]() =2
=2![]() 时,求向量
时,求向量![]() 的坐标;
的坐标;
19、(1)、设![]() 且
且![]() 在
在![]() 的延长线上,使
的延长线上,使![]() ,,则求点
,,则求点![]() 的坐标。
的坐标。
(2)、编写一个程序,对于输入的变量x的值,输出相应的y=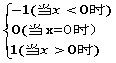 的值。
的值。
20、从10个元件中(其中4个相同的甲品牌元件和6个相同的乙品牌元件)随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为4/5,每个乙品牌元件能通过测试的概率均为3/5.试求:
(I)选出的3个元件中,至少有一个甲品牌元件的概率; (II)若选出的三个元件均为乙品牌元件,现对它们进行性能测试,求至少有两个乙品牌元件同时通过测试的概率.
21、设函数![]() ,(其中
,(其中![]() ); (Ⅰ)若f(x)的最小正周期为π,求当
); (Ⅰ)若f(x)的最小正周期为π,求当![]() 时,f(x)的值域;(Ⅱ)若函数f(x)的图象的一条对称轴方程为
时,f(x)的值域;(Ⅱ)若函数f(x)的图象的一条对称轴方程为![]() ,求
,求![]() 的值.
的值.
22、已知![]() (1)求
(1)求![]() 的解析式,并用
的解析式,并用![]() 的形式表示;(2)求方程
的形式表示;(2)求方程![]() =1的解.
=1的解.
高一第二学期·必修三与必修四综合测试题(3)参考答案
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | A | C | D | D | D | C | C | C |
17题.: (1)由已知,![]() (2)
(2)![]() ,故
,故![]()
19题、解:(1)有放回地抽取![]() 次,按抽取顺序
次,按抽取顺序![]() 记录结果,则
记录结果,则![]() 都有
都有![]() 种可能,所以试验结果有
种可能,所以试验结果有![]() 种;设事件
种;设事件![]() 为“连续
为“连续![]() 次都取正品”,则包含的基本事件共有
次都取正品”,则包含的基本事件共有![]() 种,因此,
种,因此,![]()
(2)可以看作不放回抽样![]() 次,顺序不同,基本事件不同,按抽取顺序记录
次,顺序不同,基本事件不同,按抽取顺序记录![]() ,则
,则![]() 有
有![]() 种可能,
种可能,![]() 有
有![]() 种可能,
种可能,![]() 有
有![]() 种可能,所以试验的所有结果为
种可能,所以试验的所有结果为![]() 种
种![]() 设事件
设事件![]() 为“
为“![]() 件都是正品”,则事件
件都是正品”,则事件![]() 包含的基本事件总数为
包含的基本事件总数为![]() , 所以
, 所以 ![]()
20、证明:![]() ;
; ![]() 与
与![]() 互相垂直;(2)
互相垂直;(2)![]()
![]() ;
; ![]()
![]()
![]()
![]() 而
而![]()
![]() ,
, ![]()
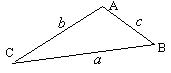 21、解:(1)如图:由
21、解:(1)如图:由![]() ;得
;得![]() ,
,![]()
∵![]() ∴
∴![]() 而
而![]() ;
;
∴![]() ; ∵
; ∵ ![]() ;
;![]() ;∵
;∵![]() ∴
∴![]() 从而
从而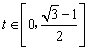
∴![]() ;
;![]() ;
;
∵![]() ;∴当
;∴当![]() 时,
时,![]() 有最大值
有最大值![]()
(2)∵![]() ; ∴
; ∴![]()
![]()
![]()
![]() ∴
∴![]()
![]() ∵
∵![]() ∴
∴![]() ; ∴
; ∴![]()
故![]() 的取值范围为
的取值范围为![]()
高一第二学期·必修三与必修四综合测试题(4)
一、 D B C D D C D A B A 11、2/5; 12、 4 ; 13、(-4, 3); 14、 1;
15、-33/65或63/65 16、[kπ+![]() ,kπ+
,kπ+![]() ], kÎZ,
], kÎZ,
17、 设P(x,y),且设l=![]() ,因为
,因为![]() 与
与![]() 方向相反,且
方向相反,且![]() =3
=3![]() ,∴ l = ―3,有
,∴ l = ―3,有![]() = ―3
= ―3![]() , ∴(x+1,y+2)=―3(3―x,2―y),
, ∴(x+1,y+2)=―3(3―x,2―y),![]()
∴ 点![]() 的坐标为(5,4);
的坐标为(5,4);
18、(1)、设事件A:两人各投一次,只有一人命中的事件为A,P(A)=0.8×(1―0.9)+0.9×(1―0.8)=0.26 , (2)、设事件B:两人各投两次,甲投中两次且乙投中一次的事件为B, P(B)=0.82×![]() ×
×![]() ×(1―0.9)=0.1152;
×(1―0.9)=0.1152;
19、(1)3/4, (2)、7/3
20、(1)、设事件A:从甲箱中任取2个产品,求这2个产品都是次品的事件, P(A)=![]() =
=![]() -
-![]() ;
;
(2)、设事件B:从甲箱中任取2个产品放入乙箱中, 然后再从乙箱中任取一个产品,是正品的事件,
①![]() :若从甲箱中任取2个放入乙箱中的是2个正品, 再从乙箱中任取一个是正品, P (
:若从甲箱中任取2个放入乙箱中的是2个正品, 再从乙箱中任取一个是正品, P (![]() ) =
) =![]()
![]() =
=![]() , ②
, ②![]() :若从甲箱中任取2个放入乙箱中的是1正品1次品, 再从乙箱中任取一个是正品, P (
:若从甲箱中任取2个放入乙箱中的是1正品1次品, 再从乙箱中任取一个是正品, P (![]() ) =
) =![]()
![]() =
=![]() , ③
, ③![]() :若从甲箱中任取2个产品放入乙箱中的是2个次品, 再从乙箱中任取一个是正品, P (
:若从甲箱中任取2个产品放入乙箱中的是2个次品, 再从乙箱中任取一个是正品, P (![]() ) =
) =![]()
![]() =
=![]() , ∴P
(B) = P (
, ∴P
(B) = P (![]() )+P (
)+P (![]() )+P (
)+P (![]() )=
)=![]() +
+![]() +
+![]() =
=![]() ;
;
21、(1)、![]() =( cos2x,
1),
=( cos2x,
1), ![]() = ( 1,
= ( 1, ![]() sin2x+2m),
sin2x+2m),![]() =
= ![]() sin2x + cos2x +2m
=2sin(2x+
sin2x + cos2x +2m
=2sin(2x+![]() )+2m,
∴ y=2sin(2x+
)+2m,
∴ y=2sin(2x+![]() )+2m; (2)、 由xÎ[0,
)+2m; (2)、 由xÎ[0,![]() ],得
],得
![]() ≤2x+
≤2x+![]() ≤
≤![]() , ―
, ―![]() ≤sin(2x+
≤sin(2x+![]() )≤1, 2m―1 ≤ 2sin(2x+
)≤1, 2m―1 ≤ 2sin(2x+![]() )+2m ≤2m +2,
)+2m ≤2m +2, ![]() =2m―1=6, ∴
=2m―1=6, ∴ ![]() =
=![]() ;
;
22、解:⑴、函数f(x)的图象过点(0,),∴-=2asin20+2sin0cos0-a,∴ a=,
∴f(x)=2sin2x+2sinxcosx-=sin2x-cos2x=2sin(2x-),
∵-1≤sin(2x-)≤1,∴函数f(x)的值域为[-2,2]。
⑵、由y =2sin[2(x-![]() m)-]=2sin(2x-m-),即函数y=2sin(2x-m-),的图象关于y轴对称,则必有 -m-=, ∴即m=--, (k∈Z且k为奇数),要使m最小,则当k=-1时,m=
m)-]=2sin(2x-m-),即函数y=2sin(2x-m-),的图象关于y轴对称,则必有 -m-=, ∴即m=--, (k∈Z且k为奇数),要使m最小,则当k=-1时,m=![]()
高一第二学期·必修三与必修四综合测试题(5)
一、C D B A C
B C B A D 11、![]() ; 12、
; 12、 ![]() ; 13、 30°; 14、
; 13、 30°; 14、![]() ;
;
15、![]() ; 16、
; 16、![]() 17、y=sin2x+cos2x+2=
17、y=sin2x+cos2x+2=![]() sin(2x+
sin(2x+![]() )+2; ①、 T=
)+2; ①、 T=![]() ; ②、 当x= kπ+
; ②、 当x= kπ+![]() (kÎZ) 时,
(kÎZ) 时,![]() =
=![]() ; ③、 [kπ―
; ③、 [kπ―![]() ,kπ+
,kπ+![]() ] ,kÎZ
] ,kÎZ
18、解: 点数对(a,b)共有6×6=36对,①,由![]() ⊥
⊥![]() 得 a―2b = 0,即a =
2b,
∴数对(a,b)只有三对:(1,2)、(2,4)、(3,6), ∴向量
得 a―2b = 0,即a =
2b,
∴数对(a,b)只有三对:(1,2)、(2,4)、(3,6), ∴向量![]() =(―1,2)、(―2,4)、(―3,6)只有3个, 此时的慨率P =
=(―1,2)、(―2,4)、(―3,6)只有3个, 此时的慨率P =![]() =
=![]() ;
②、
;
②、
![]() =
=![]() , ∴
, ∴![]() =
=![]() =2
=2![]() ,
,![]() +
+![]() =20, 又
=20, 又![]() ∥
∥![]() ,∴b = 2 a, 得
,∴b = 2 a, 得![]() =4,点数a=2,b=4, ∴向量
=4,点数a=2,b=4, ∴向量 ![]() =( 2 , 4 )
=( 2 , 4 )
19、 设分点P(x,y),∵![]() =―2
=―2![]() ,l=―2 ∴ (x―4,y+3)=―2(―2―x,6―y), x―4=2x+4,
y+3=2y―12, ∴ x=―8,y=15, ∴ P(―8,15)
,l=―2 ∴ (x―4,y+3)=―2(―2―x,6―y), x―4=2x+4,
y+3=2y―12, ∴ x=―8,y=15, ∴ P(―8,15)
20, 解:(Ⅰ)事件A:选出的3个元件中,至少有一个甲品牌元件; 则P(![]() )=
)=![]() ,
,
∴P(A)=
1-![]() ;(Ⅱ)事件B:选出的三个均为乙品牌元件,至少有两个乙品牌元件通过测试P(B)=
;(Ⅱ)事件B:选出的三个均为乙品牌元件,至少有两个乙品牌元件通过测试P(B)= ![]()
![]() =
=![]() ;
;
21, 解:![]()
![]()
![]() (Ⅰ)
(Ⅰ)![]()
![]()
![]()
(Ⅱ)![]()
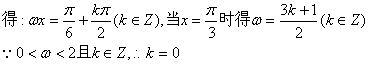
![]()
22、解:(1)![]() =
=![]()
=![]() =
=![]() =
=![]()
=![]() (2)由
(2)由![]() 得
得 ![]() =1
=1 ![]()
∴ ![]() (K
(K![]() Z) 或
Z) 或 ![]() (K
(K![]() Z
Z
所以方程的解为.
{x∣![]() ,K
,K![]() Z }
Z }