高一期末复习资料
_____班 姓名______ 高一第二学期必修三与必修四综合测试题(6)
撰稿: 方锦昌 易传庚 尹秋梅
一、选择题
1.1920°转化为孤度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(08广东文科3题)已知平面向量=(1,2),=(-2,m),且∥,则2+3= ( )
A.(-2,-4) B.(-3,-6) C.(-4,-8) D.(-5,-10)
3、(08广东文科5题)已知函数f(x)=(1+cos2x)sin3x,x∈R,则f(x)是( )
A.最小正周期为![]() 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为![]() 的偶函数
的偶函数
C.最小正周期为![]() 的奇函数 D.最小正周期为
的奇函数 D.最小正周期为![]() 的偶函数
的偶函数
4. (山东5题)(5)已知cos(α-![]() )+sinα=
)+sinα=![]() ( )
( )
(A)-![]() (B)
(B)![]() ( C ) -
( C ) -![]() (D)
(D) ![]()
5(广东理5题).在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F,若![]() 则
则![]() :
:
A.![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6.函数![]() 的图像的一条对称轴方程是( )
的图像的一条对称轴方程是( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]() D.
D.![]()
7.甲乙两人下棋,甲获胜的概率为30%,甲不输的概率为70%,则甲乙两人下一盘棋,最可能出现的情况是( )
A.甲获胜 B.乙获胜 C.二人和棋 D.无法判断
8.函数![]() 的最大值是(
)
的最大值是(
)
A.0 B.3 C.6 D.8
9. 在长为10 cm的线段AB上任取一点P,并以线段AP为边作正方形,这个正方形的面积介于25 cm2与49 cm2之间的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 10在10枝铅笔中,有8枝正品和2枝次品,从中不放回地任取2枝,至少取到1枝次品的概率是( )
10在10枝铅笔中,有8枝正品和2枝次品,从中不放回地任取2枝,至少取到1枝次品的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
11.已知向量=(2,3),=(-1,4),=-λ,=2-,若//,则λ=
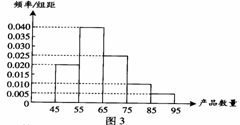
12.(08广东11题)为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为![]() ,
,![]() ,由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在
,由此得到频率分布直方图如图3,则这20名工人中一天生产该产品数量在![]() 的人数是 .
的人数是 .
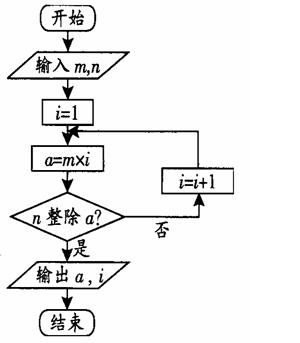
13 (08广东13题)阅读图4的程序框图,若输入m=4,n=3,则输出a=_______,i=________。
(注:框图中的赋值符号“=”,也可以写成“←”或“:=”)
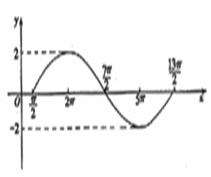 14.函数y=Asin(ωx+φ)
14.函数y=Asin(ωx+φ)![]() 部分图象如图,则函数解析式为y=________
部分图象如图,则函数解析式为y=________
15.用辗转相除法求两个数102、238的最大公约数是_____
三、解答题
16
(08广东16题13分)、已知函数f(x)=Asin(x+![]() )(A>0,0<
)(A>0,0<![]() <
<![]() ),x
),x![]() R的最大值是1,其图像经过点M
R的最大值是1,其图像经过点M![]() .(1)求f(x)的解析式;(2)已知α,β
.(1)求f(x)的解析式;(2)已知α,β![]()
![]() ,且f(α)=
,且f(α)=![]() ,f(β)=
,f(β)=![]() ,求f(α-β)的值.
,求f(α-β)的值.
17(08广东高考19题13分)某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 373 | x | y |
| 男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1) 求x的值;现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(2)
已知y![]() 245,z
245,z![]() 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.
18、(08安徽
理科17题12分)(17)已知![]()
(Ⅰ)求函数![]() 的最小正周期和图象的对称轴方程; (Ⅱ)求函数
的最小正周期和图象的对称轴方程; (Ⅱ)求函数![]() 在区间
在区间![]() 上的值域。
上的值域。
19.根据下面的要求,求满足1+2+3+…+n>500的最小的自然数n。
(Ⅰ)画出执行该问题的程序框图;
(Ⅱ)以下是解答该问题的一个程序,但有几处错误,请找出这些错误并予以更正。
 程序:i=1 S=1 n=0
程序:i=1 S=1 n=0
DO S<=500 S=S+I
i=i+1
n=n+1
WEND
PRINT n+1
END
20
(湖北16.题满分12分)已知函数f(t)=![]()
(Ⅰ)将函数g(x)化简成Asin(ωx+φ)+B(A>0,ω>0,φ∈[0,2π])的形式;(Ⅱ)求函数g(x)的值域.
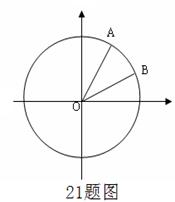
21 (08江苏高考15题).如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于
,它们的终边分别与单位圆相交于![]() 两点,已知
两点,已知![]() 的横坐标分别为
的横坐标分别为![]() ;求
;求![]() 的值 (2)求
的值 (2)求![]() 的值。
的值。
22题、在一次抗洪抢险中,准备用射击的方法引爆一个从桥上游漂流而下的一个巨大的汽油罐。已知现在手头只有五发子弹可用,且第一次命中油罐时只能使汽油流出;只有第二次再命中油罐时,油罐才能被引爆;又每次射击是相互不影响的,每次射击可命中油罐的概率是2/3。(1)问油罐最终被引爆的概率会是多少?(2)如果油罐被引爆或子弹被打光则射击停止,设射击的次数为§,求§大于或等于4的概率。
综合(6)参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | D | C | A | C | C | C | B | C |
11.λ=1/2; 12..13;13 a=12,i=3; 14. ![]() ;15. 34。
;15. 34。
16 解:(1)依题意知 A=1; ![]() , 又
, 又![]() ;
;
![]()
![]() 即
即
![]() ; 因此
; 因此 ![]() ;
;
(2)![]()
![]() ,
,![]() , 且
, 且 ![]()
![]()
![]() ,
,![]() ;
; ![]() ;
;
17解:(1)![]()
![]() ;
; ![]()
![]() (2)初三年级人数为y+z=2000-(373+377+380+370)=500, 现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为:
(2)初三年级人数为y+z=2000-(373+377+380+370)=500, 现用分层抽样的方法在全校抽取48名学生,应在初三年级抽取的人数为: ![]() 名
名
(3)设初三年级女生比男生多的事件为A ,初三年级女生男生数记为(y,z);
由(2)知 ![]() ,且
,且 ![]() ,基本事件空间包含的基本事件有:(245,255)、(246,254)、(247,253)、……(255,245)共11个事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245) 共5个;
,基本事件空间包含的基本事件有:(245,255)、(246,254)、(247,253)、……(255,245)共11个事件A包含的基本事件有:(251,249)、(252,248)、(253,247)、(254,246)、(255,245) 共5个; ![]()
![]() ;
;
18、解:(1)![]()
![]()
![]()
![]()
![]()
![]() 由
由![]()
![]() 函数图象的对称轴方程为
函数图象的对称轴方程为 ![]() (2)
(2)![]()
因为![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,所以
当
上单调递减,所以
当![]() 时,
时,![]() 去最大值 1 又
去最大值 1 又 ![]() ,当
,当![]() 时,
时,![]() 取最小值
取最小值![]() ,所以 函数
,所以 函数 ![]() 在区间
在区间![]() 上的值域为
上的值域为![]()
20题解:(Ⅰ)![]()
![]()
![]()
![]()
![]()
![]() =
=![]() (Ⅱ)由
(Ⅱ)由![]() 得
得![]()
![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数, 又
上为增函数, 又![]() (当
(当![]() ),即
),即![]() 故g(x)的值域为
故g(x)的值域为![]()
21解:由条件得![]() ,
, ![]() 为锐角,故
为锐角,故![]() 。同理可得
。同理可得![]() ,因此
,因此![]() 。(1)
。(1)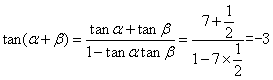 。
。
(2)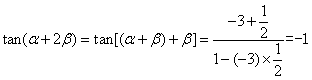
![]()
![]() ,从而
,从而![]() 。
。
22题:(1); (2)