姓名_______ 班级____班 高一第二学期数学测验试卷
学号:_______号 高一数学测验试卷 (测验内容:必修四 第二章 平面向量) (2008年3月底)
撰稿: 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题:(5×10=50′)
1.给出下面四个命题:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中正确的个数为 ( )(A)1个 (B)2个 (C)3个 (D)4个
。其中正确的个数为 ( )(A)1个 (B)2个 (C)3个 (D)4个
2、对于向量![]() ,
,![]() ,则 ( )
,则 ( )
(A)![]() ∥
∥![]() (B)
(B)![]() ⊥
⊥![]() (C)
(C)![]() 与
与![]() 的夹角为60° (D)
的夹角为60° (D)![]() 与
与![]() 的夹角为30°
的夹角为30°
3、在下面给出的四个函数中,既是区间![]() 上的增函数,又是以
上的增函数,又是以![]() 为周期的偶函数的是 ( )
为周期的偶函数的是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 4、给出向量
4、给出向量![]() =(2,1),
=(2,1),![]() =(3,4),则向量
=(3,4),则向量![]() 在向量
在向量![]() 方向上的投影为 ( )
方向上的投影为 ( )
(A)![]() (B)2 (C)
(B)2 (C)![]() (D)10、
(D)10、
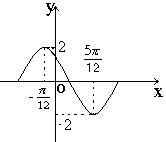
5、函数![]() 在一个周期内的图象如右所示,则此函数的解析式为( )(A)
在一个周期内的图象如右所示,则此函数的解析式为( )(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6.向量![]() ,且
,且![]() 与
与![]() 的夹角为锐角,则
的夹角为锐角,则![]() 的取值范围为 ( )
的取值范围为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、当![]() =
=![]() ,且
,且![]() 与
与![]() 不共线时,
不共线时,![]() +
+![]() 与
与![]() -
-![]() 的关系为( )
的关系为( )
A.平行 B.垂直 C.相交但不垂直 D.相等
8、若平面向量![]() 与向量
与向量![]() =(1,-2)的夹角是180o,且|
=(1,-2)的夹角是180o,且|![]() |=3
|=3![]() ,则
,则![]() =( )
=( )
A.(-3,6) B.(3,-6) C.(6,-3) D.(-6,3)
 9、已知
9、已知![]() 、
、![]() 是夹角为60°的两个单位向量,则
是夹角为60°的两个单位向量,则![]() =2
=2![]() +
+![]() 与
与![]() =-3
=-3![]() +2
+2![]() 的夹角是( ) A.30° B.60° C.120° D.150°
的夹角是( ) A.30° B.60° C.120° D.150°
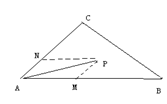
10、如图,点P是△ABC内一点,且=+,则△ABP的面积与△ABC的面积之比是( ) A、 1:5 B、2:5 C 、1:2 D、 2:1
二.填空题:
11、向量![]() 与
与![]() 共线,则
共线,则![]() = ;
= ;
12、已知![]() ,则
,则![]() = ;
= ;
13、函数![]() 的值域是
的值域是![]() ;
;
14、已知点A(-2,0),点B(3,0),动点P(x,y)满足·=x2,则动点P的轨迹方程为____
15、设![]() ,
,![]() ,
,![]() 为任意非0向量,且相互不共线,则下列命题中是真命题的序号为_______
为任意非0向量,且相互不共线,则下列命题中是真命题的序号为_______
(1)(![]() ·
·![]() )·
)·![]() -(
-(![]() ·
·![]() )·
)·![]() =0
(2)
=0
(2)![]() -
-![]() <
<![]() -
-![]() ;
;
(3)( ![]() ·
·![]() )·
)·![]() -(
-(![]() ·
·![]() )·
)·![]() 不与
不与![]() 垂直 (4)(3
垂直 (4)(3![]() +2
+2![]() )(3
)(3![]() -2
-2![]() )=9
)=9![]() 2-4
2-4![]() 2
2
三.解答题:
16、已知向量![]() =(6,2),
=(6,2),![]() =(-3,k),问当k为何值时,有:(1)、
=(-3,k),问当k为何值时,有:(1)、![]() ∥
∥![]() ?
?
(2)、![]() ⊥
⊥![]() ? (3、
? (3、![]() 与
与![]() 所成角θ是钝角 ?
所成角θ是钝角 ?
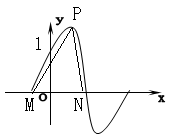
17题、如图,函数y=2sin(πx+j),(x∈R)(其中0≤j≤![]() )的图象与y轴交于点(0,1);①、求j的值;②、设P为图象上的最高点,M,N是图象与x轴的交点,求与的夹角。
)的图象与y轴交于点(0,1);①、求j的值;②、设P为图象上的最高点,M,N是图象与x轴的交点,求与的夹角。
18.
| |
(2)设向量![]() ,其中
,其中![]() ,若
,若![]() ,试求
,试求![]() 的取值范围.
的取值范围.
19、已知函数![]() 的图象在
的图象在![]() 轴右侧的第一个最大值点和最小值点分别为
轴右侧的第一个最大值点和最小值点分别为![]() 和
和![]() . (1)试求
. (1)试求![]() 的解析式; (2)将
的解析式; (2)将![]() 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的![]() (纵坐标不变),然后再将新的图象向
(纵坐标不变),然后再将新的图象向![]() 轴正方向平移
轴正方向平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.写出函数
的图象.写出函数![]() 的解析式,(3)、写出函数
的解析式,(3)、写出函数![]() 的一个单调递增区间,同时写出它的对称轴方程和对称中心坐标。
的一个单调递增区间,同时写出它的对称轴方程和对称中心坐标。
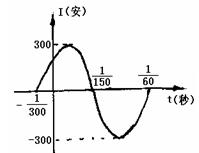
20、.如图,表示电流强度I与时间t的关系式![]() 在一个周期内的图象 :⑴、试根据图象写出
在一个周期内的图象 :⑴、试根据图象写出![]() 的解析式;⑵、为了使
的解析式;⑵、为了使![]() 中t在任意一段
中t在任意一段![]() 秒的时内I能同时取最大值A和最小值-A,那么正整数
秒的时内I能同时取最大值A和最小值-A,那么正整数![]() 的最小值为多少?
的最小值为多少?
21、如图在长方体![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的点,
上的点,![]() ,
,
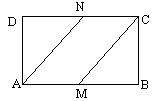 (1)若
(1)若![]() 是
是![]() 的中点,求证:
的中点,求证:![]() 与
与![]() 共线;(2)在线段
共线;(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与
与![]() 垂直?若不存在请说明理由,若存在请求出
垂直?若不存在请说明理由,若存在请求出![]() 点的位置;
点的位置;
(3)若动点![]() 在长方体
在长方体![]() 上运动,试求
上运动,试求![]() 的最大值及取得最大值时
的最大值及取得最大值时![]() 点的位置。
点的位置。
参考答案:
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | B | A | D | B | A | C | A |
11、![]() = -6 ;12、 -3
;13、
= -6 ;12、 -3
;13、![]() [-1,3] ;14、y2=x+6 15、((2)(4))
[-1,3] ;14、y2=x+6 15、((2)(4))
16题解:(1),k=-1; (2), k=9; (3), k<9, k≠-1;
17题解:(1)、j=![]() ;(2)、夹角的余弦值为
;(2)、夹角的余弦值为
18.
| |
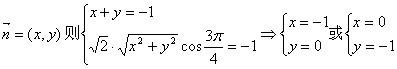
![]() ;(2)
;(2)![]() ;
;![]()
![]() =
=![]() =
=![]() =
=![]() ;∵ ―1≤sinx≤1, ∴0≤
;∵ ―1≤sinx≤1, ∴0≤![]() ≤2
≤2
19、(1)由题意可得:∵ ![]() ,
, ![]() ,∴
,∴![]() ;
;![]() 函数图像过(
函数图像过(![]() ,2),
,2), ![]() ,
, ![]() ,
,![]() ,
,![]() ;(2)依题意得
;(2)依题意得![]() ;
;
20、(1)、图象的解析式为:![]() ;(2)、要使t在任意一段
;(2)、要使t在任意一段![]() 秒能取得最大值和最小值,必须使得周期T
秒能取得最大值和最小值,必须使得周期T![]() ; 即
; 即![]() ;由于
;由于![]() 为正整数,故
为正整数,故![]() 的最小值为629
的最小值为629
21、解:(1)证明:∵![]() ;
; ![]() ∴
∴![]()
∴![]() 与
与![]() 共线;(2)解:在线段
共线;(2)解:在线段![]() 上存在点
上存在点![]() ,满足条件。设
,满足条件。设![]() ;
;![]() ∵
∵![]() 与
与![]() 垂直 ∴
垂直 ∴![]() ;即
;即![]() ∵
∵![]() ∴
∴![]() ;∴存在满足条件的点
;∴存在满足条件的点![]() ,即
,即![]() ,使得
,使得![]() 与
与![]() 垂直。 (3)解:①当
垂直。 (3)解:①当![]() 在线段
在线段![]() 上时,设
上时,设![]() ;则:
;则:![]() ;∴
;∴![]() 的最大值为
的最大值为![]() ②当
②当![]() 在线段
在线段![]() 上(不含端点)时,设
上(不含端点)时,设![]() ;∵
;∵![]() ∴
∴![]() ③当
③当![]() 在线段
在线段![]() 上时,设
上时,设![]()
![]() ; ∴
; ∴![]() 的最大值为
的最大值为![]() ; ④当
; ④当![]() 在线段
在线段![]() 上时,
上时,![]() 综上得:
综上得:![]() 的最大值是
的最大值是![]() 。
。