高一（上）数学期中考试试卷
出卷人：李 谧
一．选择题：（5＇×10）
1．已知集合M={
},集合N={
}，则M
( )。
（A）{
}
（B）{
}
（C）{
}
（D）
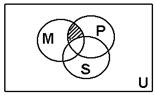
2.如图，U是全集，M、P、S是U的三个子集，则阴影部分所表示的集合是（ ）
（A）（M
（B）（M
（C）（M
P）（CUS）
（D）（MP）
（CUS）
3．已知全集U=R，A
U，BU，如果命题P：
，则命题非P是（ ）
（A）
（B）
（C）
（D）
4．下列函数中，值域为R+的是（ ）
（A）y=5
（B）y=(
)1-x
（C）y=
（D）y=
5. 化简（1+2
）（1+2
）（1+2
）(1+2-
)（1+2
），结果是（ ）
（A）
（1-2）-1 （B）（1-2）-1
（C）1-2
（D）（1-2）
6．设偶函数f(x)的定义域为R，当x
时f(x)是增函数，则f(-2),f(
),f(-3)的大小关系是（ ）
（A）f()>f(-3)>f(-2) （B）f()>f(-2)>f(-3)
（C）f()<f(-3)<f(-2) （D）f()<f(-2)<f(-3)
7．条件p∶x=x，条件q∶x2≥－x，则p是q的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
8．如果函数y=x2+ax-1在区间[0，3]上有最小值-2，那么a的值是（ ）
（A）
2 （B）-
（C）-2 （D）2或-
9．在命题“若抛物线y=ax2+bx+c的开口向下，则{
}
”的逆命题、否命题、逆否命题中结论成立的是（ ）
（A）都真 （B）都假 （C）否命题真 （D）逆否命题真
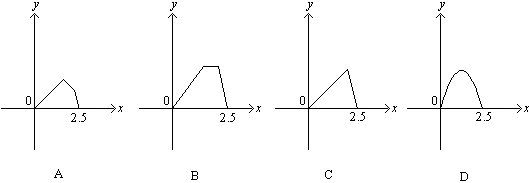
10．点P在边长为1的正方形ABCD的边上运动, 设M是CD边的中点, 则当P沿着A—B—C—M运动时, 以点P经过的路程x为自变量, 三角形APM的面积为y的函数y = f(x)的图象形状大致是( )
二．填空: （5＇×5）
11．已知
；则
。
12．
13. 化简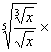
×
=
。
14．函数y=3
的单调递减区间是
。
15．有下列命题：①设映射
，则
中每一个元素不一定在
中都有原象与它对应；②命题“矩形不是四边形”是简单命题；③原命题：“能被
整除的数能被
整除”的逆命题是真命题；④甲为乙的充分条件，丙为乙的充要条件，丁为丙的必要条件，那么甲是丁的必要条件。⑤设
，
，则函数
的单调递减区间是
。其中正确的是
.（把正确答案的序号填在横线上）
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 得分 |
二．填空题答案栏（5＇×5）
11． 12． 13． 14． 15．
三．解答题：（5×12＇+15＇）
16．(本大题满分12分)
（1）求函数y=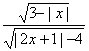
的定义域
（2）计算：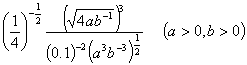
17．(本大题满分12分) 已知函数
(1)作出其图像；
(2)由图像指出函数的单调区间；
(3)由图像指出当x取何值时，函数有最值，并求出最值．
 |
18．)已知集合
，
，其中
，集合
，全集
。
（1）若
，求
的值；
（2）若
，求
。
19．
，
若
是
的充分不必要条件，求实数
的取值范围。
20．已知函数f(x)=
。
（1）求f(x)的值域；
（2）判断并证明f(x)的单调性
21．(本大题满分12分)已知函数
对一切实数x，y都满足
，且
。
（1）求
的值； （2）求的解析式；
（3）当
时，
恒成立，求实数a的取值范围。
。
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | B | A | A | A | C | .D | A |
二、填空题
11．-2
12．.f（x）＝x2－1（x≥1）.（注：无定义域者不得分）
13． 1
14．（0，+
）
15．①⑤
三、解答题
16．（1）
或
（2） 
17．(1)解：函数可化为
4分
图象如图． 6分
(2)解：由图象可以看出，函数的单调递减区间是
(－∞，1]，单调递增区间是[1，＋∞)．
18．(3)解：由图象可以看出，当x＝1时函数有最小值，且最小值为0．
解：（1）
由
可知
或
（2）
故
18．.由 。得
：
或
所以得：
解得：
20.（1）(-1,1)
（2）f(x)=
，
,且x1<x2,f(x1)-f(x2)=
<0,(∵22x1
<22x2)∴f(x)为增函数。
21. （1）令
得：
（2）令
得：
（3）由（2）知：
即
令
∵
故