高一（上）数学期末质量测试
（人教版必修1、2）
说明：
本试卷分第Ⅰ卷（选择填空题）和第Ⅱ卷（解答题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至6页，满分100分，考试时间90分钟。
第I卷 （选择填空题 满分48分）
一、选择题（本大题共12小题，每小题3分，满分36分．在每小题给出的四个选项中，只有一项是符合题目要求的）．
1．若
，
，则
（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
2、下列式子中成立的是 （ ）
A、
B、
C、
D、
3、已知函数
，当
时是增函数，当
时是减函数，则
（ ）
A.13 B.-3 C.7 D.由m的值而定的常数
4．若函数f(x)=x3(x∈R)，则函数y=f(-x)在其定义域上是 （ ）
A．单调递减的偶函数 B.单调递减的奇函数
C．单凋递增的偶函数 D．单调递增的奇函数
5、空间两条直线
与直线
都成异面直线，则的位置关系是
（ ）
A、平行或相交 B、异面 C、平行 D、平行、相交或异面
6.直线
，直线
与
平行，且直线
与垂直，则
（ ）
A.4 B.3 C.2 D.1
7、已知直线：
与圆
：
，则直线与的位置
关系是 （ ）
A、与相切
B、与相交且过的圆心
C、与相离
D、与相交且不过的圆心
8、实数a、b、c是图像连续不断的函数
定义域中的三个数，且满足
，则函数在区间（a,c）上零点的个数为
（
）
A.2 B.奇数 C.偶数 D.至少是2
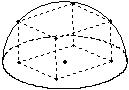9.如下图，一个正四棱柱的底面棱长为2，高为
，其下底面位于半球的大圆上，上底面四个顶点都在半球面上，则其上底面相邻两顶点间的球面距离为
（ ）
A. 
B. 
C. 
D. 
10．已知
为
上的减函数，则满足
的实数
的取值范围是（ ）
A．
B．
C．
D．
11、在直角坐标系中，已知两点
，沿轴把直角坐标平面折成直二面
角后，
两点的距离为
（ ）
A、
B、
C、
D、
12. 已知曲线C：(x-1)2+y2=1,点A(-1,0)及点B(2,a),从点A观察点B,要使视线不被曲线C拦住，则a的取值范围为 （ ）
A．(-∞,-1)∪(1,+∞)
B．( -∞,-
)∪(,+∞)
C．(,+∞)
D． ( -∞,-3)∪(3,+∞)
二、填空题（本大题共4小题，每小题3分，满分12分）．
13、函数
的定义域是
．
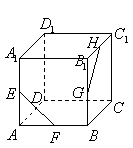
14．如图，在正方体
中，
分别为
，
，
，
的中点，则异面直线
与
所成的角等于＿＿＿＿
15已知圆
，过点A(1，0)与圆相切的直线方程为 ．
16．若函数
是奇函数,则
的值是_______
第Ⅱ卷（解答题 满分52分）
三、解答题（本大题共6小题，满分52分．解答应写出文字说明．证明过程或演算步骤）．
17（本小题满分7分）
如图，已知三角形的顶点为
，
，
，求：
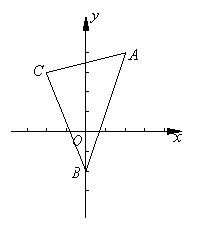（Ⅰ）AB边上的中线CM所在直线的方程；
（Ⅱ）求△ABC的面积．
18. （本小题满分7分）
已知函数是R上的增函数, 证明函数
在区间
上是增函数.
19．（本小题满分8分）
已知某几何体的俯视图是如图5所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．
(1)求该儿何体的体积V；
(2)求该几何体的侧面积S
20．（本小题满分10分）
如图，在三棱锥
中，侧面
与侧面
均为等边三角形，
，
为
中点．
（Ⅰ）证明：
平面
；
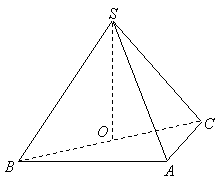（Ⅱ）求二面角
的余弦值．
21、（本小题满分10分）
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
某地西红柿从2月1日起开始上市，通过市场调查，得到西红柿种植成本Q（单位：元/102kg）与上市时间t（单位：天）的数据如下表
（1）根据上表数据，从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系，
，
（2）利用你选取的函数求西红柿种植成本最低时的上市天数及最低种植成本。
22. （本小题满分10分）
已知圆O：
和定点A(2,1)，由圆O外一点
向圆O引切线PQ，切点为Q且满足
．
(1) 求实数a、b间满足的等量关系；
(2) 求线段PQ长的最小值；
(3) 若以P为圆心所作的圆P与圆O有公共点，试求半径取最小值时圆P的方程．
答案
一选择题
DDABDB DDB C CB
二填空题
13 .
14. 
15 .
或
16. 2
三.解答题
17．（Ⅰ）解：AB中点M的坐标是
，
中线CM所在直线的方程是
，
即
（Ⅱ）解法一： 
，
直线AB的方程是
，
点C到直线AB的距离是
所以△ABC的面积是
．
解法二：设AC与
轴的交点为D，则D恰为AC的中点，其坐标是
，
18.证明: 设
.
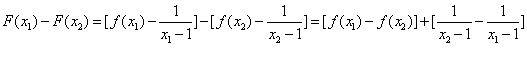
是R上的增函数,
是上的增数,
又
.故函数在区间上是增函数.
19. 解： (1)由题目知道该几何体是一个四棱锥
其体积V=
SH=
864=64
(2)该几何体的四个侧面是两对全等的三角形
其斜高分别为
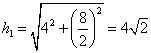
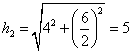
故侧面面积S=58+64=40+24
20．证明：（Ⅰ）由题设
，连结
，
为等腰直角三角形，所以
，且
，又
为等腰三角形，故
，且
，从而
．
所以
为直角三角形，
．
又
．
所以平面．
（Ⅱ）
取
中点
，连结
，由（Ⅰ）知
，得
．
为二面角的平面角．
由
得
平面
．
所以
，又
，
故
．
所以二面角的余弦值为
21、解：（1）由题意知，任意描述均应
，而此时，
均为单调函数，这与表格所提供的数据不吻合，
所以选取二次函数
进行描述。
4分
（2）由表格提供的数据代入得：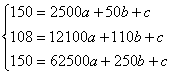
2分
2分
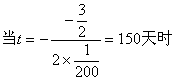，西红柿种植成本最低为
1分
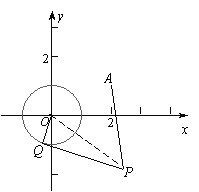22解：（1）连
为切点，
，由勾股定理有
.
又由已知
，故
.
即：
.
化简得实数a、b间满足的等量关系为：
.
（2）由
，得
.
=
.
故当
时，
即线段PQ长的最小值为
解法2：由(1)知，点P在直线l：2x + y－3 = 0 上.
∴ PQ min = PA min ，即求点A 到直线 l 的距离.
∴ PQ min = = .
（3）设
P 的半径为
，
P与O有公共点，O的半径为1，
即
且
.
而
，
故当
时，
此时, 
，
.
得半径取最小值时P的方程为
．
解法2： P与O有公共点，P半径最小时为与O外切（取小者）的情形，而这些半径的最小值为圆心O到直线l的距离减去1，圆心P为过原点与l垂直的直线l’ 与l的交点P0.
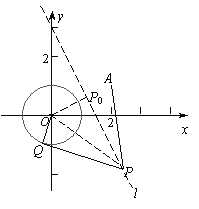r = －1 = －1.
又 l’：x－2y = 0,
解方程组
，得
.即P0( ,).
∴ 所求圆方程为