高一数学第二学期期中测试
数学试卷
（考试时间：120分钟 满分：150分 ）
说明：1．本卷分第Ⅰ卷(选择题)，第Ⅱ卷(填空题与解答题)，第Ⅰ卷选择题的答案涂在答题卡上，学生只要交答题卡和第Ⅱ卷．
第Ⅰ卷
一、 选择题（12小题，每小题5分，共60分．）
1．等差数列
的前
项和为
，若
A．12 B．10 C．8 D．6
2.在
中，
，则A等于
A
3. 设
是非零实数，若
，则下列不等式成立的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
4.在中,
,则此三角形解的情况是
A.两解 B.一解 C.一解或两解 D.无解
5．等比数列
中，
，则
等于
Ａ．
Ｂ．
Ｃ．
Ｄ．
6. 设
，
，则
=
A．
B．
C．
D．
7.在中,若
,则是
A. 等腰三角形 B. 直角三角形
C. 等腰或直角三角形 D. 钝角三角形
8. 在
高的山顶处，测得山脚处一塔顶
与塔底
的俯角分别为
与
，则塔高
等于
(A
) 
(B)
(C) 
(D) 
9. 数列{an}的通项公式是a n =
(n∈N*)，若前n项的和为
，则项数为
A．12 B．11 C．10 D．9
10.在R上定义运算
：
，若不等式
对任意实数
成立，则a的取值范围为
A．
B．
C．
D．
11.某人朝正东方向走千米后，向右转
并走3千米，结果他离出发点恰好
千米，那么的值为
(A) (B)
(C) 或 (D) 3
12.数列{an}中，已知对任意正整数n，a1＋a2＋a3＋…＋an=2n－1，则a12＋a22＋a32＋…+an2等于
(A) 
(B)
(C)
(D) 
二.填空题（本题共4小题，每小题5分，共20分）
13.在△ABC中,若a2+b2<c2,且sinC=
,则∠C=
.
14. 若数列的前
项和Sn=n2-10n（n=1，2，3，…），则此数列的通项公式为 ；数列
中数值最小的项是第 项．
15．若函数f(x) = 
的定义域为R，则a的取值范围为_______.
16. 如图，它满足①第n行首尾两数均为n，②表中的递推关系类似杨辉三角，则第n行
第2个数是
. 。
第一行 ………………… 1
第二行 ………………… 2 2
第三行 ………………… 3 4 3
第四行 ………………… 4 7 7 4
第五行 ………………… 5 11 14 11 5
第六行 ………………… 6 16 25 25 16 6
肥城一中2007—2008学年度第二学期期中测试
数学试卷
二、填空题:（每题4分,共16分）
13、_________ 14、________，_______ 15、__________ 16、__________
三.解答题（本题共6小题，共72分，解答应写出文字说明、证明过程或推演步骤）
17．(12分) 已知不等式
的解集为A，不等式
的解集为B。
（1）求A∩B；
（2）若不等式
的解集为A∩B，求不等式
的解集。
解：
18．(12分)在△ABC中，BC＝a，AC＝b，a，b是方程
的两个根，
且
。
求：(1)角C的度数；
(2)AB的长度。
解：
19．(12分)已知是等差数列，其中
（1）求的通项;
（2）数列从哪一项开始小于0;
（3）求a1+a3+a5+…+a19值。
解：
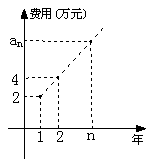20．（12分）某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用
的信息如下图。
（1）求；
（2）引进这种设备后，第几年后该公司开始获利；
（3）这种设备使用多少年，该公司的年平均获利最大？
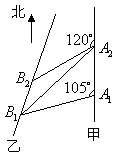
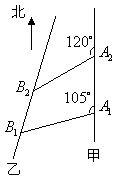21. (13分) 如图，甲船以每小时
海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于
处时，乙船位于甲船的北偏西
方向的
处，此时两船相距
海里，当甲船航行分钟到达
处时，乙船航行到甲船的北偏西
方向的
处，此时两船相距
海里，问乙船每小时航行多少海里？
22．(13分) 设数列满足
，
．
（Ⅰ）求数列的通项；
（Ⅱ）设
，求数列
的前项和
．
答案
CACAC DBACD CA
13.120o 14. an
=2n-11，3 15.[-1，0]
16. 
17.解：（1）由得
，所以A=（-1，3） ……2分
由得
，所以B=（-3，2），
……4分
∴A∩B=（-1，2） ……6分
（2）由不等式的解集为（-1，2），
所以
，解得
……9分
∴
，解得解集为R.
……12分
18. 解：（1）
C＝120°……4分
（2）由题设：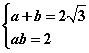
……7分
……11分
……12分
19.解：（1）
……4分
（2） 
∴数列从第10项开始小于0 ……8分
（3）
是首项为25，公差为
的等差数列，共有10项
由（2）可得：前五项为正，后五项为负。
其和
=
=
……12分
20.解：（1）由题意知，每年的费用是以2为首项，2为公差的等差数列，求得：
…………2分
（2）设纯收入与年数n的关系为f(n),则：
…………4分
由f(n)>0得n2-20n+25<0 解得
…………6分
又因为n
,所以n=2,3,4,……18.即从第2年该公司开始获利 …………8分
（3）年平均收入为
=20-
…………10分
当且仅当n=5时，年平均收益最大.所以这种设备使用5年，该公司的年平均获利最大。 …………12分
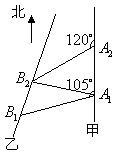21.解法一：如图，连结
，由已知
，
，
，
…………2分
又
，
是等边三角形，
…………4分
，
由已知，
，
，
…………6分
在
中，由余弦定理，
．
．
…………10分
因此，乙船的速度的大小为
（海里/小时）．…………12分
答：乙船每小时航行海里．
…………13分
解法二：如图，连结
，由已知
，，
，
，
．
在
中，由余弦定理，
．
．
由正弦定理
，
，即
，
．
在
中，由已知
，由余弦定理，
．
，
乙船的速度的大小为海里/小时．
答：乙船每小时航行海里．
22.解: (I)
…………2分
…………5分
验证
时也满足上式，
…………6分
(II) 
，
…………8分
…………10分
，
…………13分