高一数学第二学期期中测试卷
一、选择题:(每题5分,共70分)
1、不等式![]() 的解集为
.
的解集为
.
2、在△ABC中,![]() 则
则![]() .
.
3、等差数列![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() .
.
4、已知![]() ,则
,则![]() 与
与![]() 的大小关系是
.
的大小关系是
.
5、![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,若
,若![]() 成等比数列,且
成等比数列,且![]() ,则
,则![]() .
.
6、已知数列![]() 的前n项和
的前n项和![]() ,则通项
,则通项![]() .
.
7、已知等比数列中连续的三项为![]() .
.
8、在![]() 中,若
中,若![]() ,
,![]() ,那么这三角形的外接圆周长为 .
,那么这三角形的外接圆周长为 .
9、 ![]() .
.
10、在数列![]() 中,
中, ![]() ,则
,则![]() 等于______ _.
等于______ _.
11、函数![]() 的值域为_________ ___.
的值域为_________ ___.
12、已知![]() ,则不等式
,则不等式![]() 的解集为
.
的解集为
.
13、已知函数![]() 满足
满足![]() ,
,![]() ,且对任意的正整数
,且对任意的正整数![]() 都有
都有![]() ,则
,则![]() .
.
14、 定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为5,那么这个数列的前21项和
,公和为5,那么这个数列的前21项和![]() 的值为__
.
的值为__
.
二、解答题:(共90分)
15、 (14分) 根据下列条件解三角形:
(1)![]() ;(2)
;(2)![]() .
.
16、(15分)⑴ 已知正数x、y满足2x+y=1,求![]() 的最小值及对应的x、y值.
的最小值及对应的x、y值.
⑵ 若正数x、y满足2x+y-xy=0,求x+y的最小值.
17、(15分)在△ABC中,已知![]() 、
、![]() 、
、![]() 分别是角A、B、C的对边,不等式
分别是角A、B、C的对边,不等式![]() 对一切实数
对一切实数![]() 恒成立.
恒成立.
(1)求角C的最大值;(2)若角C取得最大值,且![]() ,求角B的大小.
,求角B的大小.
18、(15分)已知{an}为等差数列,![]() ,其前n项和为
,其前n项和为![]() ,若
,若![]() ,
,
(1)求数列{an}的通项;(2)求![]() 的最小值,并求出相应的n值.
的最小值,并求出相应的n值.
19、(15分)某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;
②总纯收入获利最大时,以8万元出售该渔船. 问哪种方案最合算?
20、定义:若数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列![]() 中,
中,![]() ,且
,且![]() 其中
其中![]() 为正整数.
为正整数.
(1)设![]() 证明:数列
证明:数列![]() 是“平方递推数列”,且数列
是“平方递推数列”,且数列![]() 为等比数列;
为等比数列;
(2)设(1)中“平方递推数列” ![]() 的前
的前![]() 项之积为
项之积为![]() ,即
,即![]()
![]() ,求数列
,求数列![]() 的通项及
的通项及![]() 关于
关于![]() 的表达式;
的表达式;
(3)记![]() ,求数列
,求数列![]() 的前
的前![]() 项之和
项之和![]() ,并求使
,并求使![]()
![]() 的
的![]() 的最小值.
的最小值.
高一数学期中测试参考答案
一、填空题:
1、(-1,1) ; 2、1200; 3、27; 4、![]() ; 5、
; 5、![]() ;
;
6、![]() ; 7、
; 7、![]() ; 8、2π; 9、
; 8、2π; 9、![]() ; 10、
; 10、![]() ;
;
11、![]() ; 12、
; 12、![]() ; 13、900,600; 14、52 。
; 13、900,600; 14、52 。
二、解答题:
15、解:(1)![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]() 为锐角, ∴
为锐角, ∴![]() ,∴
,∴![]() .
.
(2)![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴当![]() ;
;
∴当![]() ;
;
所以,![]()
![]() .
.
16、解:(1)因为正数x、y满足2x+y=1,
所以![]()
当且仅当![]() 时取等号。 由
时取等号。 由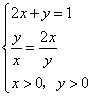 得
得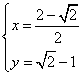
所以当![]() ,
,![]() 时
时![]() 有最小值为
有最小值为![]() 。
。
(2)
由正数x、y满足2x+y-xy=0得![]()
所以![]()
当且仅当![]() 时取等号。由
时取等号。由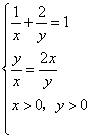 得
得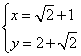
所以当![]() ,
,![]() 时
时![]() 有最小值为
有最小值为![]() 。
。
17、解:(1)由条件知,当![]() 时,不合题意。
时,不合题意。
当![]() 时,
时,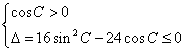 即
即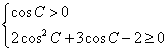
![]()
![]() 为
为![]() 的内角,
的内角,![]() 。所以角C的最大值为
。所以角C的最大值为![]() 。
。
(2) 由(1)得![]() ,
,![]() ,
,![]() ,
,![]()
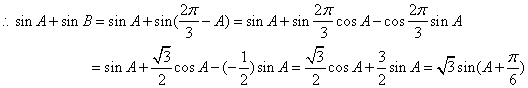
![]() ,
,![]() ,
,![]()
即![]() 的取值范围是
的取值范围是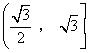 。
。
(3) 由(1)得![]() ,
,![]() 。由
。由![]() 得
得![]()
![]()
![]()
![]()
18、解:(1)由![]() 及
及![]() 得
得![]() ,解得
,解得![]()
所以![]()
(2)令![]() ,即
,即![]() 得
得![]() 。又n为正整数,
。又n为正整数,
所以当![]() 时
时![]() 。
。
所以当n=6时,![]() 最小。
最小。![]() 的最小值为
的最小值为![]()
或者先求出![]() 的表达式,再求它的最小值。
的表达式,再求它的最小值。
(3) 由(2)知数列![]() 中前6项为负数,从第7项开始为正数。所以
中前6项为负数,从第7项开始为正数。所以
当![]() 时,
时,![]()
![]()
当![]() 时,
时,![]()
![]()
所以![]()
19、解:由题设知每年的费用是以12为首项,4为公差的等差数列。
设纯收入与年数的关系为f(n),则
![]()
(1)由f(n)>0得![]()
又∵n∈N*,∴n=3,4,……17。即从第3年开始获利.
(2)①年平均收入为![]()
当且仅当n=7时,年平均获利最大,总收益为12×7+26=110(万元)
②f(n)=-2(n-10)2+102 ∵当n=10时,![]() ,
,
总收益为102+8=110(万元) 但7<10
∴第一种方案更合算。
20、(1)由条件得:![]() ,
,
![]() ,
,![]() 是“平方递推数列”。
是“平方递推数列”。
由![]() 为等比数列。
为等比数列。
(2![]()
![]()
![]() 。
。
![]()
![]() 。
。
(3)![]() ,
,
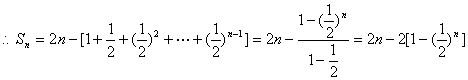
![]() 。
。
由![]() 得
得![]() ,
,
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,因此
,因此![]() 的最小值为1005。
的最小值为1005。