高一数学第二学期期中考试题
本卷分选择题和非选择题两部分，满分150分.考试用时间120分钟.
注意事项：
1． 考生务必将自己的姓名．班级．学校用蓝．黑墨水钢笔签字笔写在答题卷上；
2． 选择题．填空题每小题得出答案后，请将答案填写在答题卷相应指定位置上。答在试题卷上不得分；
3． 考试结束，考生只需将答题案交回。
第一部分 选择题(共50分)
一．选择题（本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．cos24°cos36°－sin24°sin36°的值等于( ) B
A． 0 B. 
C. 
D.-
2. f (x)=
x 3+3 x 2+2，若f ¢(－1)=4，则的值为（ ）D
A．
B．
C．
D．
3. 直线
经过原点和点(－1,－1),则直线的斜率是 ( ) A
A．
B． 
C． 
D． 
4. 已知扇形
的周长是6cm，该扇形的中心角是1弧度，则该扇形的面积（ ）A
A．2 
B．3 C．4 D．6
5. 已知sin(
+
)=
,则cos(－
)的值为( ) A
A．
B．-
C．
D．-
6. 等比数列
中，公比
，且前四项和为1，那么前八项之和为（ ）B
A．15 B．17 C．19 D．21
7. 已知
是第三象限角且sin
4+ cos 4=
,则sin •cos 的值等于( ) A
A. 
B. - C. 
D. -
8. 已知y = f(x)是偶函数，当x > 0时，f(x) = (x－1)2；若当
时，n≤f(x)≤m恒成立，则m－n的最小值是（ ）C
A． B． C．1 D．
9. 数列满足
的前n项和，则S21为（ ）A
A．
B．
C．6
D．10
10.已知函数
对于一切实数
均有
成立,且
,则当
时,不等式
恒成立时,实数的取值范围是( ) D
A．
B．
C．
D．
第二部分 非选择题(共100分)
二．填空题(每小题5分,共20分)
11. 在等差数列{n}中, 已知3＋11＝40, 则6＋7＋8＝__________．60
12. 已知角的终边经过点P（-8m, -3 ），且cos= -
，则m=
．
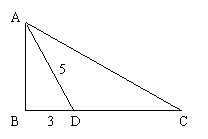
13.如右图：直角三角形ABC中，∠B是直角，AD是∠BAC
的平分线，又AD=5，AB=4，求sin∠BAC= ．
14.设
是等比数列
的前
项和, 对于等比数列,有命题
若
成等差数列,则
成等差数列成立；对于命题
：若
成等差数列, 则
________________成等差数列.请将命题补充完整,使它也是真命题.(只要一个符合要求的答案即可)
开放题，答案不唯一.
三．解答题（共80分）
15．(本小题满分12分)已知tan=2, 求
的值；
解：=
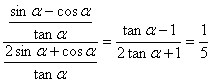………12分
16．(本小题满分12分)设
是公比大于1的等比数列，为数列的前项和．已知
，且
构成等差数列．
求数列的通项公式和
解： 由已知得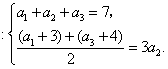
………2分
解得
．………4分
设数列的公比为，由，可得
．………6分
又，可知
，
即
， ………8分
解得
． ………9分
由题意得
．
．
………10分
故数列的通项为
． 
………12分
17. (本小题满分14分)已知为锐角，且
．
（Ⅰ）求
的值；
（Ⅱ）若cos (2－
)=－,为锐角,求cos的值．（注：原试卷中”sin (2－)=－”，改为”cos (2－)=－”）
解：（Ⅰ）由 ，为锐角 得
且
………2分
∴
且
………4分
（Ⅱ）由（Ⅰ）得
，
………6分
又cos
(2－)=－可知
………8分
∴sin (2－)=
………10分
………14分
18. (本小题满分14分)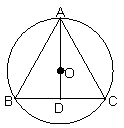 
2．如图：在半径为2
的圆内，作内接等腰三角形ABC，当底边上高为多少时三角形ABC的面积最大
？并求出此时三角形的面积。
解
设圆内接等腰三角形的底边长为2x,高为h，
那么h=AO+BO=2+
,解得
x2=h(4－h),于是内接三角形的面积为
S=x·h=
从而
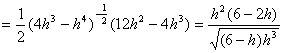
令S′=0,解得h=3,由于不考虑不存在的情况，所在区间(0,4)上列表如下
| h | (0,2) | 2 | ( |
| S′ | + | 0 | － |
| S | 增函数 | 最大值 | 减函数 |
,4)由此表可知，当
=3时，等腰三角形面积最大 此时
答 当底边上高为3时，等腰三角形面积最大，此时三角形的面积为
。
19. (本小题满分14分)已知函数
，
，
的最小值恰好是方程
的三个根，其中
．
（Ⅰ）求以上三个函数的最小值；
（Ⅱ）求证：
；
（Ⅲ）设
，
是函数
的两个极值点．
若
，求函数的解析式；
解：（Ⅰ）三个函数的最小值依次为，
，
，…………………… …3分
（Ⅱ）由，得
…………………… …4分
∴ 
，…………………… …5分
故方程
的两根是，．
故
，
．………………………7分
，即
∴ ． …………………………………………………………………8分
（Ⅲ）依题意
是方程
的根，
故有
，
，…………9分
且△
，得
．…………10分
由
；得，
，
．……………………11分
由（Ⅰ）知
，故
，………………12分
∴ 
，
………………13分
∴ 
．………………………………………………14分
20. (本小题满分14分)若对于正整数
、
表示的最大奇数因数，（例如：3的正奇数因数有1、3，所以
，又如：20的正奇数因数有1、5，所以
，）并且
,设
（Ⅰ）求S1、S2、S3 ；（注： 
）
（Ⅱ）求证：
；
（III）设
，求证数列
的前顶和
．
解：（Ⅰ）
……1分
……2分
……3分
（Ⅱ）
，
……4分
……5分
……6分
则
……7分
（Ⅲ）
……8分
……9分
……10分
……11分
当
时，
成立 ……12分
当
时，
……13分
……14分
高一数学第二学期期中考试题
二．填空题（每小题5分，共20分）
11．__________________；12．__________________；
13．__________________；14．__________________；
三．解答题（共80分）
16．（12分）
17．（12分）
18．（12分）
19．（14分）
20．（14分）
