高一数学第二学期期初考试试题

高一数学第二学期期初考试试题

高一数学试题

 (考试时间：120分钟　 总分160分)

命题人：吴春胜

A．必做题部分

一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）

1．已知角的终边经过点，则的值等于　　▲　 ．

2．当时，有　 ▲　　 ．（从中选择一个作答）

3．已知，，则　　▲　 ．

4．已知，则　　▲　 ．

5．已知向量，，且，则　　▲　 ．

6．若，，则的取值范围为　 ▲　 ．

7．已知,，与的夹角为，若，则的值为　▲　 ．

8．若、为不共线的两个向量，实数、满足，则　　▲　 ．

9．函数的单调递增区间为　  ▲　 ．

10．已知函数,存在，使恒成立，则的最小值为　　▲　 ．

11．已知，，且，则向量　　▲　 ．

12．直角△ABC中，，，若长为的线段以点为中点， 则的最大值为　　▲　 ．

13．给出下列命题：

　（1）存在实数，使；

　（2）存在实数，使；

　（3）函数是偶函数；

　（4）方程是函数图象的一条对称轴方程；

　（5）若是第一象限角，且，则tan>tan。

  （6）把函数的图象向右平移个单位，所得的函数解析式为

其中正确命题的序号是　　▲　 ．（注：把你认为正确的命题的序号都填上）

14．已知方程在内恰有两个不相等的实数根，则　　▲　 ．

　　　　　　　　　　　　　　　　 

第二学期第一次月考高一数学试题答题纸

成绩______________

注意：请把填空题的答案填在下面的横线上.

1、　　　　  　　 2、　　　　　　　 3、　　　　　　  4、　　　　　　 

 

5、　　　　　　　 6、　　　　　　　 7、　　　　　　  8、　　　　　　 

 

9、　　　　　　  10、　　　　　　  11、　　　　　　  12、　　　　　　 

 

13、　　　　　　  14、　　　　　　 

二、解答题：（本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤．）

15．（本小题满分14分）

已知函数，当时，函数的最小值为2，求函数的最大值.　

16．（本小题满分14分）

已知向量，_，与、的夹角相等，且，求向量的坐标

17．（本小题满分14分）

已知

（1）求的夹角；

（2）求实数，使垂直.

18．（本小题满分14分）

已知函数，在同一周期内，最高点的坐标为（2，2），最低点的坐标为（8，-4）

(1)　求、的值；

(2)　求函数的解析式；

(3)　求函数的周期（直接写出答案，不要求写出过程）

19．（本小题满分16分）

设G、H分别为非等边三角形ABC的重心与外心，A(0，2)，B（0，－2）且(λ∈R). （1）求证：点的坐标满足方程（；）

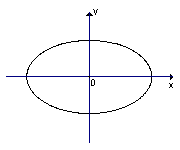
（2）若直线过点(2，0)，与曲线（图象如图所示）相交于M、N两点，设，是否存在这样的直线，使四边形OMPN为矩形？若存在，求出直线的方程；若不存在，试说明理由.

[20．（本小题满分18分）

已知为锐角三角形，， ，（）

(1) 比较与的大小并给出证明；

(2) ，角是的一个内角，比较与1的大小并给出证明.

B．附加题部分

三、附加题部分（本大题共10小题, 每小题3分，共30分.）

注意：请同学们做完上述考题后，再认真检查一遍，估计一下你的得分情况。如果你全卷得分低于96分，则本附加题部分的得分将计入全卷总分，但计入后全卷总分最多不超过96分；如果你全卷得分已经达到或超过96分，则本附加题部分的得分不计入全卷总分。

21．角的终边在第　　▲　 象限.　

22．弧度等于　　▲　 度.　

23．函数是　　▲　 函数.（填奇偶性）

24．函数的周期为　　▲　 .

25．函数的最大值为　　▲　 .

26．若，，则　　▲　 .

27．若，则　　▲　 .

28．若，，则　　▲　 .

29．若，，，则　　▲　 .

30．若，，，则　　▲　 .

注意：请把附加题的答案填在下面的横线上.

21、　　　　　　　 22、　　　　　　  23、　　　　　　  24、　　　　　　　

 

25、　　　　　  　 26、　　　　　　  27、　　　　　　  28、　　　　　　 

 

29、　　　　　　  30、