高一数学第二学期第三学段试题(期中)
数学试题(必修模块三 适用北师大版教材)
(试题录入: 陕西省渭南吝店中学 郝进) hao－
参考分式: 2008-4-23
样本数据x1,x2,…, xn的标准差 
线性回归方程系数公式: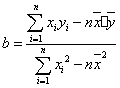 
, 
考生须知:
1.本试题共4页, 考试时间为100分钟.试题由第Ⅰ卷(基本题满分100分)和第Ⅱ卷(附加题20分)组成.基本题为每个学生必答题, 附加题由学有余力的学生选用.
2.在答题前,同学们务必在答题卡上填上你的学校、班级、姓名、学号.
3.答题时请同学们在答题卡上做答,考试结束时只交答题卡.
第Ⅰ卷(基本题 满分100分)
一、选择题(本大题共8个小题,每小题4分,共32分)
1.把总体中的N个个体的代号写在形状、大小相同的签上,然后将这些均匀搅拌,每次随机地从中抽取一个,然后将签均匀搅拌,现进行下一次抽取,这种方法属于( )
A. 分层抽样 B.简单随机抽样 C. 系统抽样 D.以上都不正确
2.某班有48名同学,春游前,班长把全班同学对春游地的意向绘制成了扇形统计图,其中,"想去秦岭太白山的同学数"对应的扇形圆心角为60°,则下列说法正确的是( )
A.想去秦岭太白山的同学占全班同学的
.
B.想去秦岭太白山的同学占全班同学的60%
C.想去秦岭太白山的同学肯定最多
D.想去秦岭太白山的同学有12人
3.任何一个算法都必须有的基本结构是( )
A.顺序结构 B. 条件结构 C. 循环结构 D. 三个都有
4.口袋内装有一些大小相同的红球、白球和黑球,从中摸出红球的概率是0.26,摸出黑球的概率是0.61,则摸出白球的概率是( )
A. 0.87 B. 0.61 C. 0.26 D. 0.13
5.从学号1~50的高一某班50名学生中随机选取5名同学参加数学测试, 采用系统抽样的方法, 则所选5名学生的学号可能是( )
A. 1,2,5,6,9 B. 5,15,25, 35,45 C. 3,5,13,15,25 D. 1,11,23,35,47
6.如果算法程序框图如右图,那么输出的S等于( )
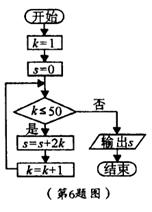
A. 2550 B. 2601 C. 2500 D. 2551
7.已知一组数据: －1,x,0,1,－2的平均数是0, 那么,这组数据的标准差是( )
A. 
B.2 C. 4 D. 10
8.抛掷两颗骰子, 则点数之和出现7点概率为( )
A. B. 
C. 
D. 
二、填空题(本大题共4小题,每小题5分, 共20分)
9.甲、乙两人做出拳游戏(锤子、剪刀、布),则平局的概率为
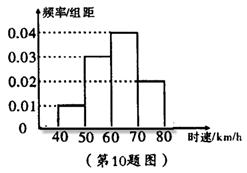
10.200辆汽车通过某一段公路时的时速频率分布直方图如图所示,则时速在[50,60)的汽车大约有 辆
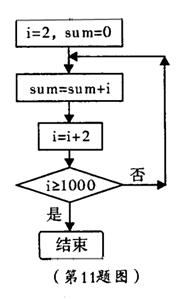
11.给出下面的算法程序框图,那么其循环体执行的次数是 .
12. 对总数为n的一批零件抽取一个容量为30的样本,若每个零件被抽到的概率为0.25, 则n
三、解答题(本大题4小题,共48分,解答写出文字说明,证明过程或演算步骤)
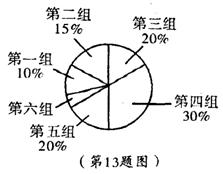
13.(12分)在学校开展的综合实践活动中,某班全班同学分成6个小组, 各小组上交作品如图所示,其中第二组上交了12件.
(1)本次活动共有多少作品参加评比?
(2)哪一组上交的作品数最多?有多少件?
(3)经评比,第四组和第六组分别有10件、2件作品获奖,则这两组中哪一组获奖率较高?
14.(12分)口袋里有若干红球、黄球与蓝球, 随机从中摸一个球,摸到红球的概率为0.40, 摸到黄球的概率为0.30, 求:
(1)摸出的一个为红球或黄球的概率;
(2)摸出的一个为蓝球的概率.
15.(12分)下表是某小卖部6天卖出可乐的数量与当天平均气温的对比表:
| 气温/°C | －1 | 4 | 10 | 13 | 18 | 26 |
| 数量(个) | 20 | 24 | 34 | 38 | 50 | 64 |
(1)将上表中的数据制成散点图;
(2)求线性回归方程系数a、b.
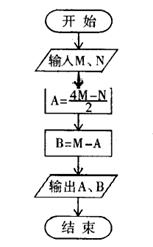
16.(12分)我国古算术中有一个鸡兔同笼问题, 请完成下列一个算法:
(1)输入鸡和兔的总数量M;
(2)输入鸡和兔的总数量N;
(3)鸡的数量A= ;
(4)兔的数量B= ;
写出程序框图.
第Ⅱ卷 (附加题 满分20分)
四、附加题(本大题共2小题,共20分)
17.某商场为了促销,采用购物打折的优惠办法: 每位顾客一次购物:
①在1000元及以上且2000元以下者按九五折优惠;
②在2000元以上且3000元以下者按九折优惠;
③在3000元以上且5000元以下者按八五折优惠;
④在5000元及以上者按八折优惠.
(1)写出函数关系式;
(2)试编写流程图求优惠价.
18. 甲、乙两人独立地破译1个密码, 他们能译出密码的概率分别为和, 求:
(1)甲、乙两人至少有一个人破译出密码的概率;
(2)两人都没有破译出密码的概率.
陕西普通高中新课程教学质量检测学段考试
数学试题(必修模块三 适用北师大版教材)
一、选择题(本大题共8个小题,每小题4分,共32分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | A | A | D | B | A | A | C |
二、填空题(本大题共4小题, 每小题5分,共30分)
9. 10. 60 11. 499 12. 120
三、解答题(本大题4小题, 共48分.解答写出文字说明,证明过程或演算步骤)
13.解: (1) 12÷15%=80 (件) (4分)
(2) 第四组: 30%÷15%×12=24 (件) (8分)
(3)第四组作品数为24件, 获奖率为10÷24≈41.7%.
第六组作品数为80×(1－20%-30%-20%-15%-10%)=4(件) 获奖率为2÷4=50%, 所以,第六组获奖率较高. (12分)
14. 解: (1) 0.7 (6分) (2) 0.30 (12分)
15. 解: (1) (4分)
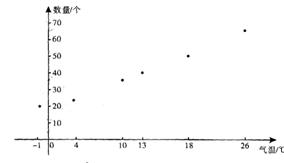
(2) 
, 
, 
=1+16+100+169+324+676=1286.
=－20+96++26×64=3474 (8分) 
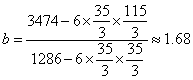
a≈18.73 (12分)
16. 解: A= (3分) B=M－N (6分) 程序框图:
四、选作题 (本大题2小题,共20分)
17.解: 设购物款数原为x元, 优惠后人格为y元, 则优惠付款方式可用分段函数表示为
(1) 
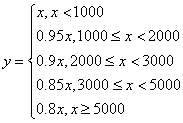(5分)
(2)用流程图表示为:
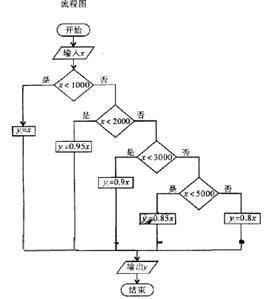
18. 解(1)设甲破译密码的事件为A, 乙破译密码的事件为B, 则 P(A+B)=P(A)+P(B)= + = 答: 至少有一个人破译出密码的概率为 (5分)
(2)设两人都没有破译的事件为C, 则P(C)=1－P(A+B)=1－ =
答: 两人都没有破译出密码的概率为 (10分)
其他解法参照以上评分标准评分.