高一数学必修2练习题(四)
4.1圆的方程 4.2直线、圆的位置关系 4.3空间直角坐标系
A组题(共100分)
一.选择题:本大题共有5小题,每小题7分,共35分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1、已知两点A(9,4)和B(3,6),则以AB为直径的圆的方程为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2、如果直线x-my+2=0与圆![]() 有两个不同的交点,则
有两个不同的交点,则
(A)m≥![]() (B)m>
(B)m>![]() (C)m<
(C)m<![]() (D)m≤
(D)m≤![]()
3、在空间直角坐标系中点P(1,3,-5)关于![]() 对称的点的坐标是( )
对称的点的坐标是( )
(A)(-1,3,-5) (B)(1,-3,5)
(C)(1,3,5) (D)(-1,-3,5)
4、若圆![]() ,
,![]() ,则
,则![]() 和
和![]() 的位置关系是
的位置关系是
(A)外离 (B)相交 (C)内切 (D)外切
5、方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值依次为
(A)2、4、4; (B)-2、4、4; (C)2、-4、4; (D)2、-4、-4
二.填空题:本大题共有4小题,每小题6分,共24分.把答案直接填在答题卷相应题的横线上.
6、设M是圆![]() 上的点,则M到直线
上的点,则M到直线![]() 的最长距离是
.
的最长距离是
.
7、过点P(-1,6)且与圆![]() 相切的直线方程是________________.
相切的直线方程是________________.
8、设直线![]() 和圆
和圆![]() 相交于点A、B,则弦AB的垂直平分线方程是
.
相交于点A、B,则弦AB的垂直平分线方程是
.
9、.圆心在直线![]() 上的圆C与
上的圆C与![]() 轴交于两点
轴交于两点![]() ,
,![]() ,则圆C的方程为 .
,则圆C的方程为 .
三.解答题:本大题共3小题,共41分.解答应写出文字说明,证明过程或演算步骤.
10、(本小题满分13分)
一圆与![]() 轴相切,圆心在直线
轴相切,圆心在直线![]() 上,在
上,在![]() 上截得的弦长为
上截得的弦长为![]() ,求此圆的方程.
,求此圆的方程.
11、(本小题满分14分)
已知点P(-1,0)与Q(1,0),且动点M满足![]() ,求点M的轨迹方程,并说明轨迹是什么图形.
,求点M的轨迹方程,并说明轨迹是什么图形.
12、(本小题满分14分)
已知圆C:![]() 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
B组题(共100分)
一.选择题:本大题共有5小题,每小题7分,共35分.在每小题给出的四个选项中,有且只有一项是符合题目要求的。
1、1.方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)表示圆方程,则t的取值范围是
A.-1<t<![]() B.-1<t<
B.-1<t<![]()
C.-![]() <t<1
D.1<t<2
<t<1
D.1<t<2
2、已知A(3,3,1),B(1,0,5),则到A、B两点距离相等的点P(x,y,z)的坐标x,y,z满足的条件是
(A)4x-6y-8z-7=0 (B)4x-6y-8z+7=0
(C)4x+6y-8z-7=0 (D)4x+6y-8z+7=0
3、已知直线ax+by+c=0(abc≠0)与圆x2+y2=1相切,则三条边长分别为|a|、|b|、
|c|的三角形
A.是锐角三角形 B.是直角三角形
C.是钝角三角形 D.不存在
4、M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是
A、相切 B、相交 C、相离 D、相切或相交
5、两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为
A.-1 B.2 C.3 D.0
二.填空题:本大题共有4小题,每小题6分,共24分.把答案直接填在答题卷相应题的横线上.
6、过圆x2+y2-x+y-2=0和x2+y2=5的交点,且圆心在直线3x+4y-1=0上的圆的方程为
.
7、将圆x2+y2=1按向量a平移得到圆(x+1)2+(y-2)2=1,则a的坐标为____________.
8、圆x2+y2+x-6y+3=0上两点P、Q关于直线kx-y+4=0对称,则k=____________.
9.若直线y=x+k与曲线x=![]() 恰有一个公共点,则k的取值范围是___________.
恰有一个公共点,则k的取值范围是___________.
三.解答题:本大题共3小题,共41分.解答应写出文字说明,证明过程或演算步骤.
10、(本小题满分13分)
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
11、(本小题满分14分)
已知圆C:![]() ,直线l:
,直线l:![]() (m∈R). (Ⅰ)证明:不论m取什么实数,直线l与圆恒交于两点.
(m∈R). (Ⅰ)证明:不论m取什么实数,直线l与圆恒交于两点.
(Ⅱ)求直线被圆C截得的弦长最小时l的方程.
12、(本小题满分14分)
设有半径为3![]() 的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
C组题(共50分)
一.填空题:把答案直接填在答题卷相应题的横线上.
1、曲线![]() 与直线
与直线![]() 有两个交点时,实数
有两个交点时,实数![]() 的取值范围是
.
的取值范围是
.
2、已知直线![]() 与圆O:则
与圆O:则![]() 相交于A、B两点,且AB=
相交于A、B两点,且AB=![]() ,则
,则![]() =
.
=
.
二.解答题:
3、.圆![]() 内有一点P(-1,2),AB过点P,
内有一点P(-1,2),AB过点P,
① 若弦长![]() ,求直线AB的倾斜角
,求直线AB的倾斜角![]() ;
;
②若圆上恰有三点到直线AB的距离等于![]() ,求直线AB的方程.
,求直线AB的方程.
4、如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若![]() =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
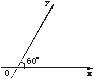
(1)若P点斜坐标为(2,-2),求P到O的距离PO;
(2)求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
答案与提示
A组:
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | A | B | C | D | B |
6.
8 7. x=-1或3x-4y+27=0 8.. ![]() 9. (x-2)2+(y+3)2=5
9. (x-2)2+(y+3)2=5
10.解:解:设所求圆的方程为![]() ,则
,则
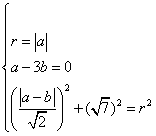 ,解得
,解得![]() 或
或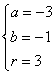 .
.
所以,所求圆的方程为![]() ,或
,或![]() .
.
11.解:设点M的坐标为(x,y),由于![]() ,则
,则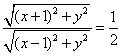 ,
,
整理得:![]() 即
即 ![]()
这就是点M的轨迹方程.图形为以(-![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆.
为半径的圆.
12.解:(1)已知圆C:![]() 的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
的圆心为C(1,0),因直线过点P、C,所以直线l的斜率为2,
直线l的方程为y=2(x-1),即 2x-y-2=0.
(2)当弦AB被点P平分时,l⊥PC, 直线l的方程为![]() , 即
x+2y-6=0
, 即
x+2y-6=0
(3)当直线l的倾斜角为45º时,斜率为1,直线l的方程为y-2=x-2 ,即 x-y=0
圆心C到直线l的距离为![]() ,圆的半径为3,
,圆的半径为3,
弦AB的长为![]() .
.
B组:
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 答案 | C | D | B | C | A |
6. (x+1)2+(y-1)2=13
7. (-1,2) 8.
2
9 -1<k≤1或k=-![]()
10.解:圆(x-2)2+(y-2)2=1关于x轴的对称方程是(x-2)2+(y+2)2=1.
设l方程为y-3=k(x+3),由于对称圆心(2,-2)到l距离为圆的半径1,从而可得k1=-![]() ,k2=-
,k2=-![]() .故所求l的方程是3x+4y-3=0或4x+3y+3=0.
.故所求l的方程是3x+4y-3=0或4x+3y+3=0.
11.解:(Ⅰ)证明:直线l:![]() 可化为
可化为
![]()
由于m∈R,则![]() ,解得
,解得![]() ,
,
∴直线l经过定点A(3,1).
又∵ 圆C的圆心坐标为(1,2),且│AC│=![]() <5(半径),
<5(半径),
∴ 点A在圆C内,
从而不论m为何值,直线l恒与圆C相交于两点.
(Ⅱ)解:要使弦长最小时,必须l⊥AC,
由kBC=-![]() ,知k1=2,m=-
,知k1=2,m=-![]() .
.
所以直线l的方程为2x-y-5=0.
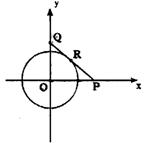
12.解:如图建立平面直角坐标系,由题意
可设A、B两人速度分别为3v千米/小时 ,
v千米/小时,再设出发x0小时,在点P改变
方向,又经过y0小时,在点Q处与B相遇.
则P、Q两点坐标为(3vx0, 0),(0,vx0+vy0).
由OP2+OQ2=PQ2知,
(3vx0)2+(vx0+vy0)2=(3vy0)2,
即![]() .
.
![]() ……①
……①
将①代入![]()
又已知PQ与圆O相切,直线PQ在y轴上的截距就是两个相遇的位置.
设直线![]() 相切,
相切,
则有![]()
答:A、B相遇点在离村中心正北![]() 千米处
千米处
C组:
1. ![]() 2.
2. ![]()
3. (1)![]() 或
或![]() ;(2)x+y-1=0或x-y+3=0.
;(2)x+y-1=0或x-y+3=0.
4.解:(1)∵P点斜坐标为(2,-2),
∴![]() =2e1-2e2. ∴
=2e1-2e2. ∴![]() 2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
2=(2e1-2e2)2=8-8e1·e2=8-8×cos60°=4.
∴![]() =2,即OP=2.
=2,即OP=2.
(2)设圆上动点M的斜坐标为(x,y),则![]() =xe1+ye2.
=xe1+ye2.
∴(xe1+ye2)2=1. ∴x2+y2+2xye1·e2=1. ∴x2+y2+xy=1.
故所求方程为x2+y2+xy=1.