高一数学必修4练习题（一）
A组题（共100分）
一．选择题：本大题共5小题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1.下列各角中与角
终边相同的是
（ ）
A.-
B.-3000
C. 
D.2400
2.角α的始边在x轴正半轴、终边过点P（3,4）,则sinα的值为 （ ）
A.
B. 
C.
D.
3. 角α的始边在x轴正半轴、终边过点P（
,y）,且cosα=
，则y的值为（
）
A.3 B. 1 C.±3 D.±1
4. 式子sin3000的值等于 （ ）
A.
B. 
C.- D.-
5. 已知tanα= -a，则tan（π-α）的值等于 （ ）
A. a B. -a C.
D.-
二．填空题：本大题共4小题，每小题6分，共24分。
6．与角-1000同终边的角的集合是 .
7．角
的终边与单位圆的交点的坐标是
.
8. 已知角α是第三象限角，且tanα=2，则sinα+cosα等于 .
9. 已知sinα+cosα>1，则α是第 象限角.
三．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
10．（本小题13分）已知
，求
+sin2x的值
11.（本小题14分）化简：
.
12.（本小题14分）已知
，
求（1）
；（2）
的值
B组题（共100分）
四．选择题：本大题共5小题，每小题7分，共35分。在每小题给出的四个选项中，只有一项是符合题目要求的。
13．设角
是第二象限角，且
，则
角的终边在（ ）
A 第一象限
B 第二象限
C 第三象限
D 第四象限
14．若是第四象限角，则
是
（ ）
A 第一象限角 B 第二象限角 C 第三象限角 D 第四象限角
15. 式子sin2cos3tan4的值 （ ）
A 小于
B 大于 C 等于
D 不存在
16. 函数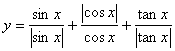
的值域是
（ ）
A 
B 
C 
D 
17. 若角α的终边落在直线x+y=0上，则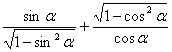
的值等于（ ）
A 
B 
C 或
D
五．填空题：本大题共4小题，每小题6分，共24分。
18．设
分别是第二象限角，则点
落在第_________象限
19．若角α与角β的终边关于y轴对称，则α与β的关系是___________
20. 设扇形的周长为
，面积为
，则扇形的圆心角的弧度数是
21. 与-20020终边相同的最大负角是_______________
六．解答题：本大题共3小题，共41分，解答题应写出文字说明、证明过程或演算步骤。
22．（本小题13分）已知
是关于
的方程
的两个实根，且
，求
的值
23．（本小题14分）已知
求
的范围
24.（本小题14分）已知
求
的值
C组题（共50分）
七．选择或填空题：本大题共2题。
25．三角形ABC中角C为钝角，则有 （ ）
A.sinA>cosB B. sinA<cosB C. sinA=cosB D. sinA与cosB大小不确定
26．已知sin（200+α）=
，则cos（1100+α）=
.
八．解答题：本大题共2小题，解答题应写出文字说明、证明过程或演算步骤。
27．一个扇形
的周长为
，试问：当扇形的半径和圆心角各取何值时，此扇形的面积最大？
28．已知
其中为锐角，求证：
.
参考答案
A组题（共100分）
一.选择题： BDCDA
二.填空题： 6.（｛α︱α=k·3600-1000，k∈Z｝），7.（（,））， 8.（-
）9．（一）
三.解答题：
10．解：
+sin2x= 
+
= 
+
= -3+
= -2
11. 解：原式
12. 解：由
得
即
（1）
（2）
B组题（共100分）
四.选择题： CCACD
五.填空题：18．（四、三、二），19．（
，k∈Z），20.（2），21.（
）
六.解答题：
22．解：
，而，则
得
，则
，
23．解：
，
24. 解：
, 
C组题（共50分）
七.选择或填空题： 25．（B） 26．（-）
八.解答题：
27．解：设扇形的半径为
，则
当
时，
取最大值，此时
28．证明：由得
即
而
，得
，即
得
而为锐角，
.
说明：
A组题：最基本要求．最高达到会考的中等要求，与课本的练习题．简单的习题对应．
B组题：中等要求．会考的中、高级要求，高考的中等要求，与课本的习题对应
C组题：高等要求．对应高考的高等要求．
其中：有些题出自王新敞的资料．