高一数学必修4练习题(二)
适用范围1.4三角函数图象与性质,1.5函数![]() 的图象,1.6三角函数模型的简单应用
的图象,1.6三角函数模型的简单应用
A组题(共100分)
一.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
![]()
![]()
![]()
![]()
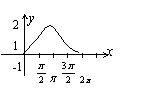
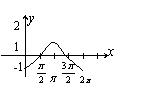
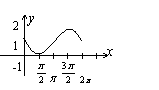
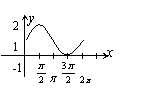 1.函数
1.函数![]() 的大致图象是( )
的大致图象是( )
|
A. B. C. D.
![]() 2. 函数
2. 函数![]() 的周期为( )
的周期为( )
A. ![]() B.
B. ![]() C.
C.![]() D.
D.![]()
![]() 3. 为了得到函数
3. 为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上各点( )
的图象上各点( )
A.向左平移![]() 个长度单位 B.向右平移
个长度单位 B.向右平移![]() 个长度单位
个长度单位
 C.向左平移
C.向左平移![]() 个长度单位 D.向左平移
个长度单位 D.向左平移![]() 个长度单位
个长度单位
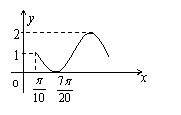
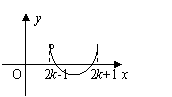
4.函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的解析式为( )
的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
5. 在下列函数中,同时满足①在![]() 上递增,②以
上递增,②以![]() 为周期,③是奇函数的函数是( )
为周期,③是奇函数的函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二. 填空题:本大题共4小题,每小题6分,共24分。
6.函数![]() 的定义域是_________________________.
的定义域是_________________________.
7.函数![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() ,则
,则![]() =_______,
=_______,![]() =_______.
=_______.
8.函数![]() 的单调递减区间是___________________.
的单调递减区间是___________________.
9. 下列函数中,①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
不是偶函数的是____________.
三. 解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.(本小题13分)已知函数![]()
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出![]() 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由![]() 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.
 |
11.(本小题14分)已知函数![]()
(1)求该函数的单调区间,最大、最小值;
(2)设![]() ,若
,若![]() 的图象关于y轴对称,求实数
的图象关于y轴对称,求实数![]() 的最小正值。
的最小正值。
12.(本小题14分)设地球表面某地正午太阳高度角为![]() ,
,![]() 为此时太阳直射纬度(北纬为正、南纬为负),
为此时太阳直射纬度(北纬为正、南纬为负),![]() 为该地的纬度值(北纬为正、南纬为负),那么这三个量之间的关系是
为该地的纬度值(北纬为正、南纬为负),那么这三个量之间的关系是![]() ,当太阳直射北回归线时,
,当太阳直射北回归线时,![]() =
=![]() ;当太阳直射南回归线时,
;当太阳直射南回归线时,![]() =
=![]() 。已知厦门市北纬24°
。已知厦门市北纬24°![]() =1.1785。(精确到
=1.1785。(精确到
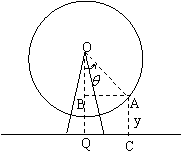
(1)如果在厦门市的一幢高h=
(2)某人想在厦门市买房,经过勘查,发现某小区的位置及楼房结构、质量都不错,但想买的楼房南面有一幢高约
 |

B组题(共100分)
四. 选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.下列不等式中,正确的是( )
A.tan![]() B.sin
B.sin![]()
C.sin(π-1)<sin1o D.cos![]()
14. 函数![]() 的单调递减区间是( )
的单调递减区间是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
15.函数![]() 的周期和对称轴分别为( )
的周期和对称轴分别为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
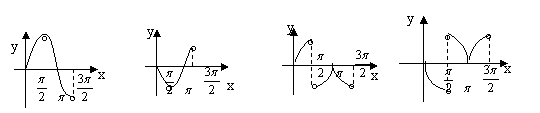 16.如图,函数
16.如图,函数![]() 的图像是( )
的图像是( )
A B C D
17.要得到函数![]() 的图象,可由函数
的图象,可由函数![]() ( )
( )
A. 向左平移![]() 个长度单位 B. 向右平移
个长度单位 B. 向右平移![]() 个长度单位
个长度单位
C. 向左平移![]() 个长度单位 D. 向右平移
个长度单位 D. 向右平移![]() 个长度单位
个长度单位
五. 填空题:本大题共4小题,每小题6分,共24分。
18. 若函数![]() 同时满足条件:①在区间
同时满足条件:①在区间![]() 内为增函数;②
内为增函数;②![]() ;③最小正周期为
;③最小正周期为![]() ,则这样的解析式为__________________.(注:填上你认为正确的一个解析式即可,不必考虑所有情况)
,则这样的解析式为__________________.(注:填上你认为正确的一个解析式即可,不必考虑所有情况)
19. 已知函数![]() ,若对任意
,若对任意![]() 都有
都有![]() 成立,则
成立,则![]() 的最小值是______________.
的最小值是______________.
20. 如果函数![]() 的图象关于
的图象关于![]() 对称,那么实数
对称,那么实数![]() 的值为_______.
的值为_______.
21.给出下列命题:
①函数![]() 不是周期函数; ②函数
不是周期函数; ②函数![]() 在定义域内是增函数;
在定义域内是增函数;
③函数![]() 的周期是
的周期是![]() ; ④函数
; ④函数![]() 是偶函数。
是偶函数。
其中正确的命题的序号是_______________.
六. 解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
22.(本小题13分)已知![]() ,且
,且![]() ,求证:对于
,求证:对于![]() ,有
,有![]() .
.
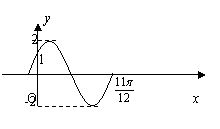
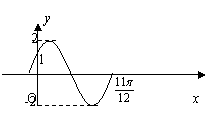
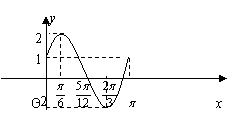
23.(本小题14分)已知函数![]() 在一个周期内的图象 下图所示。
在一个周期内的图象 下图所示。
(1)求函数的解析式;
 (2)设
(2)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
.
24.(本小题14分)如图,游乐场所的摩天轮匀速旋转,每转一周需要12min,其中心O离地面
(1)求出你与地面的距离![]() 和时间
和时间![]() (min)的函数关系式;
(min)的函数关系式;
(2)当你第四次距离地面
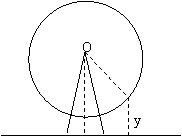 (3)当你登上摩天轮2分钟后,你的朋友也在摩天轮的最低处登上摩天轮,问你的朋友登上摩天轮多少时间后,第一次出现你和你的朋友与地面的距离之差最大?求出这个最大值。
(3)当你登上摩天轮2分钟后,你的朋友也在摩天轮的最低处登上摩天轮,问你的朋友登上摩天轮多少时间后,第一次出现你和你的朋友与地面的距离之差最大?求出这个最大值。
C组题(共50分)
七.选择或填空题:本大题共2题。
25.设![]() 是定义域为R,最小正周期为
是定义域为R,最小正周期为![]() 的函数,若
的函数,若 ,则
,则![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]() C.0
D.
C.0
D. ![]()
26. 设![]() 则
则![]() 的值域为 _______ .
的值域为 _______ .
八. 解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
27. 已知函数![]() .
.
(1)试讨论函数![]() 的奇偶性;
的奇偶性;
(2)求当![]() 取得最大值时,自变量x的取值范围.
取得最大值时,自变量x的取值范围.
.
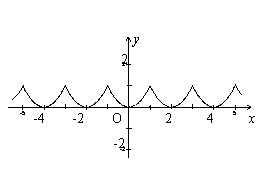
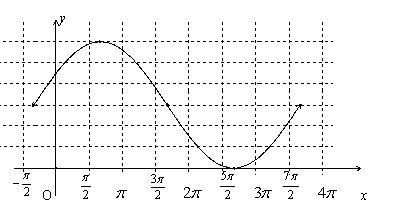
28. 设函数![]() 是定义在区间
是定义在区间![]() 上以2为周期的函数,记
上以2为周期的函数,记![]() .已知当
.已知当![]() 时,
时,![]() ,如图.
,如图.
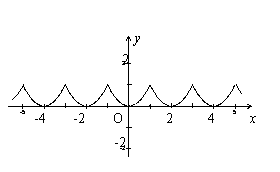 (1)求函数
(1)求函数![]() 的解析式;
的解析式;
(2)对于![]() ,求集合
,求集合![]() .
.
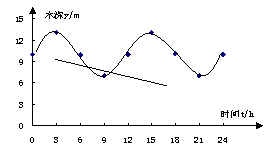
29. 某港口的水深y(m)是时间t (0≤t≤24,单位:h)的函数,下表是该港口某一天从0:00时至24:00时记录的时间t与水深y的关系:
| t(h) | 0:00 | 3:00 | 6:00 | 9:00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
| y(m) | 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
经长时间的观察,水深y与t的关系可以用![]() 拟合。根据当天的数据,完成下面的问题:
拟合。根据当天的数据,完成下面的问题:
(1)求出当天的拟合函数![]() 的表达式;
的表达式;
(2)如果某船的吃水深度(船底与水面的距离)为
(3)若某船吃水深度为
厦门市2007—2008学年数学必修4练习(二)参考答案
适用范围1.4三角函数图象与性质,1.5函数![]() 的图象,1.6三角函数模型的简单应用
的图象,1.6三角函数模型的简单应用
A组题(共100分)
一.选择题:BADDC
二.填空题:
6. ![]()
7. ![]() ,1
,1
8. ![]()
9. ②④
三.解答题:
10.解:(1)列表
| x |
|
|
|
|
|
|
| 0 |
|
|
|
|
|
| 3 | 6 | 3 | 0 | 3 |
(2)周期T=![]() ,振幅A=3,初相
,振幅A=3,初相![]() ,
,
由![]() ,得
,得![]() 即为对称轴;
即为对称轴;
(3)①由![]() 的图象上各点向左平移
的图象上各点向左平移![]() 个长度单位,得
个长度单位,得![]() 的图象;
的图象;
②由![]() 的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得
的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),得![]() 的图象;
的图象;
③由![]() 的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得
的图象上各点的纵坐标伸长为原来的3倍(横坐标不变),得![]() 的图象;
的图象;
④由![]() 的图象上各点向上平移3个长度单位,得
的图象上各点向上平移3个长度单位,得![]() +3的图象。
+3的图象。
11.解:(1)![]() =
=![]()
=![]()
当![]() 时函数递增,得
时函数递增,得![]() ,
,
所以函数的单调增区间为: ![]()
同理得函数单调减区间为:![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
(2)由(1)得![]() ,
,
![]() ,
,
![]()
![]() 的图象关于y轴对称,
的图象关于y轴对称,![]() ,
,
![]() ,
,
![]() 实数
实数![]() 的最小正值是
的最小正值是![]() 。
。
 12.解:(1)由于厦门市北纬24°
12.解:(1)由于厦门市北纬24°![]() =-
=-![]() 时,楼房向北的影子最长。
时,楼房向北的影子最长。
这时![]() =
=![]()
当h=![]() .
.
 即两楼间的距离不应小于
即两楼间的距离不应小于
(2)如图,AC=![]()
![]() ,
,
![]() ,
,
由于楼层高
B组题(共100分)
四.选择题: DCACB
五.填空题:
18. ![]() ,
,![]() ,
,![]() ,……
,……
19. 2
20. ![]() ,提示:
,提示:![]()
21.①④
六.解答题:
22. 解:![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() 在
在![]() 上为增函数,
上为增函数,![]() 在
在![]() 上为减函数,
上为减函数,
![]() ,
,
又![]()
![]() ,
,
![]() 在R上为减函数,且
在R上为减函数,且![]()
![]() ,
,
 从而
从而![]()
23. 解:(1)显然A=2,
又图象过(0,1)点,![]() ,
,
![]() ,
,![]() ;
;
由图象结合“五点法”可知,![]() 对应函数
对应函数![]() 图象的点(
图象的点(![]() ),
),
![]() ,得
,得![]() .
.
所以所求的函数的解析式为:![]() .
.
 (2)如图所示,在同一坐标系中画出
(2)如图所示,在同一坐标系中画出![]() 和
和![]() (
(![]() )的图象,
)的图象,
由图可知,当![]() 时,直线
时,直线![]() 与曲线有两个不同的交点,即原方程有两个不同的实数根。
与曲线有两个不同的交点,即原方程有两个不同的实数根。
![]() m的取值范围为:
m的取值范围为:![]() ;
;
当![]() 时,两根和为
时,两根和为![]() ;当
;当![]() 时,两根和为
时,两根和为![]() .
.
24. 解:(1)![]() 摩天轮的角速度
摩天轮的角速度![]()
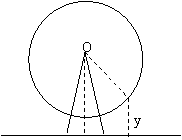
![]() 最低点的角终边OQ到与地面的距离
最低点的角终边OQ到与地面的距离![]() 的角终边OA的角
的角终边OA的角![]() ,
,
![]() ,
,
即与地面的距离![]() 与时间
与时间![]() (min)的函数关系式为
(min)的函数关系式为 ![]() ;
;
 (2)令
(2)令![]() 得
得![]() ,
,
![]() 第四次距离地面
第四次距离地面
![]() ,
,![]() ,
,
即第四次距离地面
(3)当朋友距离地面高度![]() 时,
时,
这时自己距离地面高度![]() ;
;
![]()
当两人所处位置连线垂直地面时,距离之差最大,这t=2.
即当你的朋友登上摩天轮2min后,第一次出现你和你的朋友与地面的距离之差最大;
这个最大值为
(![]() =
=![]()
=![]() =
=![]() )
)
C组题(共50分)
七.选择或填空题:
25.B
26. ![]()
八.解答题:
27. 解:(1)当![]() 时,
时,![]() 是奇函数;当
是奇函数;当![]() 时,
时,![]() 是非奇非偶的函数.
是非奇非偶的函数.
(2)
当![]() 时,
时,![]() ,
,![]() 取得最大值,这时x的取值范围为
取得最大值,这时x的取值范围为![]() ;
;
当![]() 时,
时,![]() ,
,![]() 取得最大值,这时x的取值范围为
取得最大值,这时x的取值范围为![]() ;
;
当![]() 时,
时,![]() ,
,![]() 取得最大值,这时x的取值范围为
取得最大值,这时x的取值范围为![]() .
.
 28. 解:(1)
28. 解:(1)![]() 是以2为周期的函数,
是以2为周期的函数,
![]() ,
,
当![]() 时,
时,![]() ,
,
![]()
![]() 的解析式为:
的解析式为:![]() .
.
(2)当![]() 且
且![]() 时,
时,![]() 化为
化为![]() ,
,
令![]()
![]() ,
,
则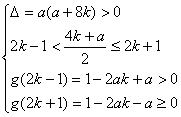
即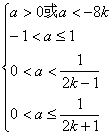
![]()
![]()
29. 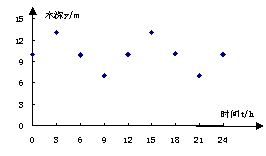 解:(1)根据数据,画出散点图,
解:(1)根据数据,画出散点图,
知A=3,h=10,T=12,
![]() ,
,![]()
![]() (2)由题意,水深y≥4.5+7,
(2)由题意,水深y≥4.5+7,
即![]() ,
,
![]() ,
,![]() ,
,
![]() 或
或![]() ;
;
所以,该船在1:00至5:00或13:00至17:00能安全进港。
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
(3)设在时刻x船舶安全水深为y,则![]() (
(![]() ),
),
这时水深![]() ,
,
若使船舶安全,则![]() ,
,
 即
即![]() ,
,
![]() ,
,
即该船在7:00必须停止卸货,驶向较安全的水域。
 y
y