高一数学必修4练习题(三)
适用范围:第二章 《平面向量》
A组题(共100分)
一.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列说法正确的是( )
A.向量![]() 与向量
与向量![]() 是共线向量,则A、B、C、D必在同一直线上
是共线向量,则A、B、C、D必在同一直线上
B.向量![]() 与
与![]() 平行,则
平行,则![]() 与
与![]() 的方向相同或相反
的方向相同或相反
 C.向量
C.向量![]() 的长度与向量
的长度与向量![]() 的长度相等
的长度相等
D.单位向量都相等
2.如图,在平行四边形ABCD中,![]() 等于( )
等于( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
3. 已知向量![]() ,
,![]() ,若
,若![]() 、
、![]() 平行且反向,则
平行且反向,则![]() 的值为( )
的值为( )
A.0 B.-![]()
4. 在正方形ABCD中,已知它的边长为1,设![]() ,则
,则![]() 的值为( )
的值为( )
A.0
B![]() D.
D.
![]()
5. 将![]() 的图象按向量
的图象按向量![]() 平移,则平移后所得图象的解析式为( )
平移,则平移后所得图象的解析式为( )
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
二.填空题:本大题共4小题,每小题6分,共24分。
6.已知![]() ,则
,则![]() =____________.
=____________.
7. 若向量![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() .
.
8.已知向量![]() ,则与
,则与![]() 垂直的单位向量的坐标是_____________.
垂直的单位向量的坐标是_____________.
9.河水的流速为![]() ,静水的速度为v,则
,静水的速度为v,则![]() =________,v=________m/s.(可用数据
=________,v=________m/s.(可用数据![]() )
)
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.(本小题13分)已知![]() ,分别求使下列结论成立的实数
,分别求使下列结论成立的实数![]() 的值:
的值:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() 的夹角是
的夹角是![]() .
.
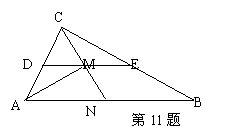 11.(本小题14分)如图,在
11.(本小题14分)如图,在![]() 中,D、E分别是AC、BC的中点,M是DE的中点,若
中,D、E分别是AC、BC的中点,M是DE的中点,若![]() .
.
(1)用![]() 表示
表示![]() ;
;
(2)若N为线段AB的中点,求证:C、M、N三点共线.
12.(本小题14分)已知![]() ,
,![]() ;
;
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
B组题(共100分)
四.选择题:本大题共5小题,每小题7分,共35分。在每小题给出的四个选项中,只有一项是符合题目要求的。
13.已知![]() 的三个顶点A、B、C及平面内一点P满足
的三个顶点A、B、C及平面内一点P满足![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. P在![]() 的内部
B. P在
的内部
B. P在![]() 的外部
的外部
C. P在边AB所在的直线上 D. P是边AC上的一个三等分点
14.(07浙江) 若非零向量![]() 满足
满足![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15. (07辽宁) 若向量![]() 不共线,
不共线,![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]() 的夹角为( )
的夹角为( )
A.0 B.![]() C.
C.![]() D.
D.![]()
16. 已知向量![]() ,若
,若![]() 与
与![]() 垂直,则
垂直,则![]() =( )
=( )
 A.
A.![]() B.
B.![]()
![]() C.
C.![]() D.4
D.4
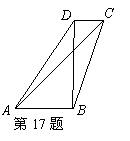
17. 如图,在四边形![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
五.填空题:本大题共4小题,每小题6分,共24分。
18.已知点A(1,0),B(0,1),若点P满足![]() ,则点P的轨迹方程是_______________________.
,则点P的轨迹方程是_______________________.
19.在![]() 中,
中,![]() ,则点O是
,则点O是![]() 的_______心.(指三角形
的_______心.(指三角形 的内心、外心、重心、垂心)
的内心、外心、重心、垂心)
20. (07陕西)如图,平面内有三个向量![]() 、
、![]() 、
、![]() ,其中与
,其中与![]() 与
与![]() 的夹角为120°,
的夹角为120°,![]() 与
与![]() 的夹角为30°,且
的夹角为30°,且![]() =
=![]() =1,
=1,![]() =
=![]() ,若
,若![]() =λ
=λ![]() +μ
+μ![]() (λ,μ∈R),则λ+μ的值为
.
(λ,μ∈R),则λ+μ的值为
.
21.对于任意的两个实数对![]() ,规定:
,规定:![]() ,当且仅当
,当且仅当![]() ;定义运算“
;定义运算“![]() ”为:
”为:![]() ,运算“
,运算“![]() ”为:
”为:![]() .
.
设![]() ,若
,若![]() ,则
,则![]() =___________.
=___________.
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
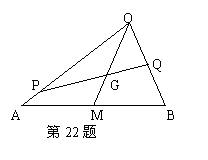 22.(本小题13分)如图,PQ过
22.(本小题13分)如图,PQ过![]() 的重心G,设
的重心G,设![]() ;若
;若![]() .求证:
.求证:![]() .
.
23.(本小题14分)(07广东)已知△![]() 顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
(1)若![]() ,求sin∠A的值;
,求sin∠A的值;
(2)若∠A是钝角,求c的取值范围.
24.(本小题14分)已知向量![]() .若存在不同时为零的实数
.若存在不同时为零的实数![]() ,使
,使![]() ,且
,且![]() .
.
(1)试求函数关系式![]() ;
;
(2)若![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围.
的取值范围.
C组题(共50分)
七.选择或填空题:本大题共2题。
25.在三角函数中,对于单位圆上任意一点![]() ,我们有
,我们有![]()
![]()
![]() ;若定义
;若定义![]() .则下列条件中,不能确定A、B、P三点共线的是(
)
.则下列条件中,不能确定A、B、P三点共线的是(
)
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
26. 已知向量![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的夹角,则
的夹角,则![]() 的取值范围是___________________.
的取值范围是___________________.
八.解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
 27.如图,在Rt△ABC中,已知BC=
27.如图,在Rt△ABC中,已知BC=![]() ,若长为2
,若长为2![]() 的线段PQ以点A为中点,问
的线段PQ以点A为中点,问![]() 与
与![]() 的夹角θ取何值时,
的夹角θ取何值时,![]()
![]() 的值最大?并求出这个最大值。
的值最大?并求出这个最大值。
28.已知二次项系数为正数的二次函数![]() 对任意的
对任意的![]() ,都有
,都有![]() ,设向量
,设向量![]() ,当
,当![]() ,求不等式
,求不等式![]() 的解集.
的解集.
29. 设点O在![]() 的内部,S表示面积。
的内部,S表示面积。
(1)若
![]() 成立,求
成立,求![]() ;
;
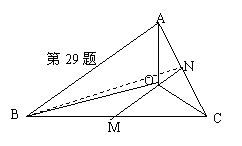 (2) 若
(2) 若![]() 成立,求
成立,求![]() .
.
厦门市2007—2008学年数学必修4练习(三)参考答案
适用范围:第二章 《平面向量》
A组题(共100分)
一.选择题:1.C 2.A 3 B
二.填空题:6. ![]() 7.
7. ![]() 8.
8. ![]() 9.
9. ![]() ,
,![]()
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
10.解:(1)![]()
![]() ,
,![]() ,即
,即![]() ;
;
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,解得
,解得![]() ;
;
(3)
![]() 的夹角是
的夹角是![]() ,
,![]()
![]() =
=![]() ,
,
化简整理得:![]() ,
,![]() .
.
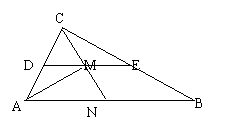 11.解:(1)
11.解:(1)![]() ,
,
![]() D、E分别是AC、BC的中点,
D、E分别是AC、BC的中点,
![]() ,
,
又M是DE的中点,
![]() ,
,
![]() .
.
(2)![]() N为线段AB的中点,
N为线段AB的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,即C、M、N三点共线。
,即C、M、N三点共线。
12. 解:(1)![]() ,
,
![]() ,
,
![]() ;
;
![]() ;
;
(2)![]() ,
,
![]() ,
,![]() ,
,
![]()
B组题(共100分)
四.选择题:13.D
解析:选D.![]()
14.C 15. D 16.C 17. C
五.18.![]() 19. 垂心
20. 6 21. (2,0)
19. 垂心
20. 6 21. (2,0)
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤。
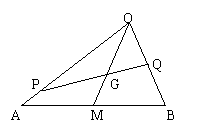 22.解:
22.解:![]() G
G![]() 的重心,
的重心,
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() 点P、G、Q共线,
点P、G、Q共线,
![]() ,
,![]() ,
,
![]()
![]() ,
,
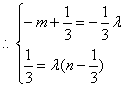
消元![]() 得:
得:![]() ,即
,即![]() .
.
23.解:(1) ![]() ,
,
当c=5时,![]() ,
,
![]() ,
,
![]() ;
;
(2)若A为钝角,则![]() ,
,
![]() ,
,
解得c>![]() ,
,
显然此时有AB和AC不共线,故当A为钝角时,c的取值范围为[![]() ,
,![]() ).
).
24.解:(1)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)设![]() ,
,
则![]() =
=![]() ,
,
![]()
![]() 在
在![]() 上是增函数,
上是增函数,![]() ,
,
又![]() ,
,![]() ,
,
即![]() 上恒成立,
上恒成立,
![]() ,
,
![]() 即为所求.
即为所求.
C组题(共50分)
七.25.D 26. ![]()
八.解答题:本大题共3小题,解答题应写出文字说明、证明过程或演算步骤。
27.解法一:∵![]() ,∴
,∴![]() 。
。
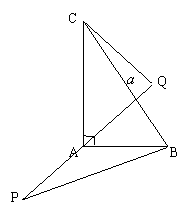 ∵
∵![]()
∴![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
故当![]() ,既
,既![]() (
(![]() 与
与![]() 方向相同)时,
方向相同)时,![]() 最大,其最大值为0。
最大,其最大值为0。
解法二:以直有项点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系。
设AB=c, AC=b,则A(0,0),B(c,0),C(0,b)
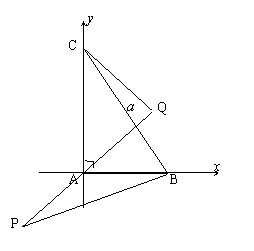 且
且![]() ,
,![]() 。
。
设点P的坐标为![]() ,则
,则![]() 。
。
∴![]() ,
,
![]() 。
。
∴![]()
=![]() 。
。
∵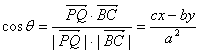 ;
;
∴![]() 。
。
∴![]() 。
。
故当![]() ,即
,即![]() (
(![]() 与
与![]() 方向相同)时,
方向相同)时,![]() 最大,其最大值为0。
最大,其最大值为0。
28.解:因为二次函数![]() 对任意的
对任意的![]() ,都有
,都有![]() ,
,
![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
又二次项系数为正数![]() 在
在![]() 上是增函数;
上是增函数;
![]() ,
,
![]() ,
,
不等式![]() 化为
化为![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
所以![]() 的解集为
的解集为![]() .
.
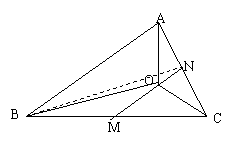 29.
解:(1)设M、N分别是BC、AC的中点,
29.
解:(1)设M、N分别是BC、AC的中点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
即M、O、N三点共线,且![]() ,
,
![]() ,
,
![]() ,
,
同理:![]() ,
,![]() ,
,
所以![]() =3:1:2.
=3:1:2.
(2)设M、N分别是BC、AC的中点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
即M、O、N三点共线,且![]() ,
,
![]() ,
,
![]() ,
,
同理:![]() ,
,
![]() ,
,
所以![]() =
=![]() ,
,
即![]() =
=![]()