高一数学必修5练习题(三)
A组题(共100分)
一.选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如果-1,a,b,c,-9成等比数列,那么( )
A b=3,ac=9 B b=-3,ac=9 C b=3,ac=-9 D b=-3,ac=-9
2.在等比数列{an}中,a1=1,a10=3,则![]() ( )
( )
A. 81
B. 27![]() C.
C. ![]() D. 243
D. 243
3.等比数列{a n }中,已知a9 =-2,则此数列前17项之积为 ( )
A.216 B.-216 C.217 D.-217
4.等比数列{an}中,a3=7,前3项之和S3=21, 则公比q的值为( )
A.1 B.-![]() C.1或-1 D.-1或
C.1或-1 D.-1或![]()
5.在等比数列{an}中,如果a6=6,a9=9,那么a3等于( )
A.4 B.![]() C.
C.![]() D.2
D.2
二.填空题:本大题共4小题,每小题6分,共24分.
6.在等比数列{an}中,已知a1=![]() ,a4=12,则q=_____ ____,an=____ ____.
,a4=12,则q=_____ ____,an=____ ____.
7.在等比数列{an}中,an>0,且an+2=an+an+1,则该数列的公比q=___ ___.
8.在等比数列{an}中,已知a4a7=-512,a3+a8=124,且公比为整数,求a10= .
9.数列{![]() }中,
}中,![]() 且
且![]() 是正整数),则数列的通项公式
是正整数),则数列的通项公式![]() .
.
三.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤.
10.已知等比数列![]() 的前n项和记为
的前n项和记为![]() a3=3 , a10=384.
a3=3 , a10=384.
求该数列的公比q和通项公式an
11.已知等比数列{an},公比为-2,它的第n项为48,第2n-3项为192,求此数列的通项公式.
12.数列{an}是正项等比数列,它的前n项和为80,其中数值最大的项为54,前2n项的和为6560,求它的前100项的和.
B组题(共100分)
四.选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
13.数列1,37,314,321,……中,398是这个数列的( )
(A)第13项 (B)第14项 (C)第15项 (D)不在此数列中
14.在公比q![]() 1的等比数列{bn}中,若bm=p,则bm+n的值为( )
1的等比数列{bn}中,若bm=p,则bm+n的值为( )
(A)pqn+1 (B)pqn-1 (C)pqn (D)pqm+n-1
15.若数列{bn}是等比数列,公比为q,则下列命题中是真命题的是( )
(A)若q>1,则bn+1>bn (B)若0<q<1,则bn+1<bn
(C)若q=1,则sn+1=Sn (D)若-1<q<0,则![]()
16.在等比数列{an}中,a9+a10=a(a![]() ),a19+a20=b,则a99+a20的值为( )
),a19+a20=b,则a99+a20的值为( )
(A)![]() (B)(
(B)(![]() )9 (C)
)9 (C)![]() (D)(
(D)(![]() )10
)10
17.在2与6之间插入n个数,使它们组成等比数列,则这个数列的公比为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
五.填空题:本大题共4小题,每小题6分,共24分.
18.在等比数列{an}中,a1-a5=-![]() ,S4=-5,则a4= .
,S4=-5,则a4= .
19.三个正数a,b,c成等比数列,且a+b+c=62,lga+lgb+lgc=3,则这三个正数为
20.某工厂在某年度之初借款A元,从该年度末开始,每年度偿还一定的金额,恰在n年内还清,年利率为r,则每次偿还的金额为 元.
21.某种细胞每隔20分钟分裂一次,一个细胞每次分裂成两个细胞,则一个细胞经过3小时20分分裂成细胞有_____个.
六.解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤.
22.已知数列满足a1=1,an+1=2an+1(n∈N*)
(1) 求证数列{an+1}是等比数列;
(2) 求{an}的通项公式.
23.四个数中,前三个数成等差数列,后三个数成等比数列,第二、第三个数之和为8,第一、第四个数之和为16,求这四个数.
24.在等比数列{an}中,已知Sn=48,S2n=60,求S3n.
C组题(共50分)
七.填空题:本大题共2题.
25.在等比数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() _________.
_________.
26.![]() 等于_________.
等于_________.
八.解答题:本大题共2小题,解答题应写出文字说明、证明过程或演算步骤.
27.某城市1990年底人口为50万,人均住房面积为16 m2,如果该市每年人口平均增长率为1%,每年平均新增住房面积为30万 m2,求2000年底该市人均住房的面积数.(已知1.015≈1.05,精确到0.01 m2)
28.在等比数列{an}中,已知对n∈N*,a1+a2+…+an=2n-1,求a12+a22+…+an2.
参考答案
A组题
一.选择题:
1.B 2.A 3.C. 4.A. 5.D.
二.填空题:
6.2, 3·2n-2. 7.![]() . 8.512 . 9.
. 8.512 . 9.![]() .
.
三.解答题:
10.解: 由a10= a3q7 得q7=128, ∴q=2 ………………………4分
又a3=3得a1q2=3 ∴ a1=![]()
∴ an=![]() ×2n-1=3·2n-3…………………………………10分
×2n-1=3·2n-3…………………………………10分
11.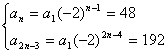
![]() 解得a1=3 ∴an=a1qn-1=3(-2)n-1 .
解得a1=3 ∴an=a1qn-1=3(-2)n-1 .
12.∵ S2n>Sn, ∴q![]() 1
1 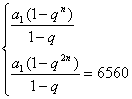
![]() ②/①,得qn=81 ③∴q>1,故前n项中an最大.③代入①,得a1=q-1
②/①,得qn=81 ③∴q>1,故前n项中an最大.③代入①,得a1=q-1
又由an=a1qn-1=54,得81a1=54q ∴a1=2,q=3 ∴S100=![]() .
.
B组题
13.C 14.C 15.D 16.A 17.C 18.1
19.50,10,2或2,10,50
20.![]()
21.1024
22..(1)证明: 由an+1=2an+1得an+1+1=2(an+1)
又an+1≠0 ∴![]() =2
=2
即{an+1}为等比数列.
(2)解析: 由(1)知an+1=(a1+1)qn-1
即an=(a1+1)qn-1-1=2·2n-1-1=2n-1
23. 解:由条件可设四数分别为![]() ,
,![]() ,
,![]() ,
,![]()
由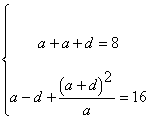 解得
解得![]() 或
或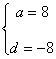 (因
(因 ![]() ,舍去)
,舍去)
![]() 四数分别是-2,2,6,18
四数分别是-2,2,6,18
24. 解析一: ∵S2n≠2Sn,∴q≠1
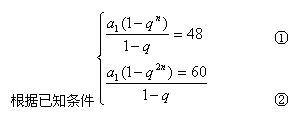
②÷①得:1+qn=![]() 即qn=
即qn=![]() ③
③
③代入①得![]() =64 ④
=64 ④
∴S3n=![]() (1-q3n)=64(1-
(1-q3n)=64(1-![]() )=63
)=63
解析二: ∵{an}为等比数列
∴(S2n-Sn)2=Sn(S3n-S2n)
∴S3n=![]() +60=63
+60=63
C组题
25. 105
26. ![]()
27. 解析:依题意,每年年底的人口数组成一个等比数列{an}:a1=50,q=1+1%=1.01,n=11
则a11=50×1.0110=50×(1.015)2≈55.125(万),
又每年年底的住房面积数组成一个等差数列{bn}:b1=16×50=800,d=30,n=11
∴b11=800+10×30=1100(万米2)
因此2000年底人均住房面积为:1100÷55.125≈19.95(m2)
28.解析: 由a1+a2+…+an=2n-1 ①
n∈N*知a1=1
且a1+a2+…+an-1=2n-1-1 ②
由①-②得an=2n-1,n≥2
又a1=1,∴an=2n-1,n∈N*
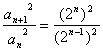 =4
=4
即{an2}为公比为4的等比数列
∴a12+a22+…+an2=![]()