高一数学必修5练习题(四)
————不等式
A组题(共100分)
一.选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
![]()
2.下列各对不等式中同解的是( )
A.![]() 与
与 ![]() B.
B.![]() 与
与 ![]()
C.![]() 与
与![]() D.
D.![]() 与
与 ![]()
3.若![]()
![]()
![]() ,则函数
,则函数![]() 的值域是(
)
的值域是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.如果![]() ,那么,下列不等式中正确的是( )
,那么,下列不等式中正确的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.如果实数![]() 满足
满足![]() ,则
,则![]() 有 ( )
有 ( )
A.最小值![]() 和最大值1
B.最大值1和最小值
和最大值1
B.最大值1和最小值![]()
C.最小值![]() 而无最大值
D.最大值1而无最小值
而无最大值
D.最大值1而无最小值
二.填空题:本大题共4小题,每小题6分,共24分
6.二次方程![]() ,有一个根比
,有一个根比![]() 大,另一个根比
大,另一个根比![]() 小,
小,
则![]() 的取值范围是 ____________.
的取值范围是 ____________.
7.一个两位数的个位数字比十位数字大![]() ,若这个两位数小于
,若这个两位数小于![]() ,
,
则这个两位数为________________.
8.某公司一年购买某种货物400吨,每次都购买![]() 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为![]() 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则![]() _______
吨.
_______
吨.
9.当![]() ______时,函数
______时,函数![]() 有最_______值,且最值是_________.
有最_______值,且最值是_________.
三、解答题:(本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤)
10.解不等式![]()
![]()
11.不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
12.求![]() 的最大值,使式中的x、y满足约束条件
的最大值,使式中的x、y满足约束条件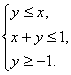
B组题(共100分)
一 选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.一元二次不等式![]() 的解集是(
的解集是(![]() ,
,![]() ),则
),则![]() 的值是( ).
的值是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.设集合![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知直线l过点P(2,1),且与x轴、y轴的正半轴分别交于A、B两点,O为坐标原点,则三角形OAB面积的最小值为 ( )
A.4 B.3 C.2 D.5
4.下列各函数中,最小值为2的是 ( )
A.![]() B.
B.![]() ,
,![]()
C.![]() D.
D.![]()
5.如果![]() ,则
,则![]() 的最大值是 ( )
的最大值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题6分,共24分).
6.设正实数x、y满足![]() ,则
,则![]() 的取值范围是___________.
的取值范围是___________.
7.若![]() 的解集是
的解集是![]() ,则
,则![]() 的值为___________.
的值为___________.
8.当![]() 时,函数
时,函数![]() 的最小值是________.
的最小值是________.
9.设![]() 且
且![]() ,则
,则![]() 的最小值为________.
的最小值为________.
三、解答题:(本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤)
10.(1)已知实数![]() 、
、![]() 满足
满足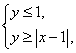 求
求![]() 的最大值.
的最大值.
(2)已知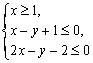 求
求 ![]() 的最小值.
的最小值.
11.若a,b,c>0且a(a+b+c)+bc=4-![]() ,求2a+b+c的最小值.
,求2a+b+c的最小值.
12.设函数![]() 的值域为
的值域为![]() ,求a,b的值.
,求a,b的值.
C组题(共100分)
一.选择题:本大题共5题,每小题7分,共35分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若方程![]() 只有正根,则
只有正根,则![]() 的取值范围是( ).
的取值范围是( ).
A.![]() 或
或![]() B.
B. ![]()
C.![]() D.
D. ![]()
2.若关于![]() 的不等式
的不等式![]() ≤
≤![]() +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数![]() ,总有( )
,总有( )
A.2∈M,0∈M B.2![]() M,0
M,0![]() M C.2∈M,0
M C.2∈M,0![]() M
D.2
M
D.2![]() M,0∈M.
M,0∈M.
3.若a>0,b>0,则不等式-b<![]() < a等价于( )
< a等价于( )
A.![]() <x<0或0<x<
<x<0或0<x<![]() B.-
B.-![]() <x<
<x<![]() C.x<-
C.x<-![]() 或x>
或x>![]() D.x<
D.x<![]() 或x>
或x>![]()
4.若不等式![]() 有唯一解,则
有唯一解,则![]() 的取值为( )
的取值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.不等式组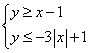 的区域面积是( )
的区域面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题6分,共24分).
6.不等式![]() 的解集是_______________.
的解集是_______________.
7.若![]() 且
且![]() 则
则![]() 的最大值为________.
的最大值为________.
8.设![]() ,则函数
,则函数![]() 在
在![]() =________时,有最小值__________.
=________时,有最小值__________.
9.已知函数f(x)= ax2 + 2ax + 4 (a>0),若x1< x2 , x1+x2=0 , 则f(x1)与f(x2)的大小关系为__________.
三、解答题:本大题共3小题,共41分,解答题应写出文字说明、证明过程或演算步骤.
10.求函数![]() 的最小值.
的最小值.
11.甲、乙两地相距skm, 汽车从甲地匀速行驶到乙地,速度不得超过ckm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的二次方成正比,且比例系数为b,固定部分为a元.
(1)把全部运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大的速度行驶?
12.已知不等式![]()
(I)求t,m的值;
(2)若函数f(x)=-x2+ax+4在区间![]() 上递增,求关于x的不等式loga(-mx2+3x+2—t)<0的解集.
上递增,求关于x的不等式loga(-mx2+3x+2—t)<0的解集.
厦门市2007—2008学年数学必修5练习(四)参考答案
A组题(共100分)
1.D 2.B 3.B 4.A 5.B 6 . -1<a<0 7.13或24
8. 解:某公司一年购买某种货物400吨,每次都购买![]() 吨,则需要购买
吨,则需要购买![]() 次,运费为4万元/次,一年的总存储费用为
次,运费为4万元/次,一年的总存储费用为![]() 万元,一年的总运费与总存储费用之和为
万元,一年的总运费与总存储费用之和为![]() 万元,
万元,![]() ≥160,当
≥160,当![]() 即
即![]() 20吨时,一年的总运费与总存储费用之和最小.
20吨时,一年的总运费与总存储费用之和最小.
9. ±1,大,1
10.解: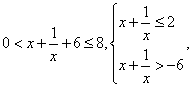 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
![]()
11.解:![]()
当![]() 时,
时,![]() 并不恒成立;
并不恒成立;
当![]() 时,则
时,则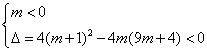
得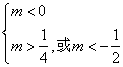
![]()
12. 作出可行域 ![]()
B组题(共100分)
1.D 2.B 3.A 4.D 5.D 6 .[1,+∞) 7. 2 8. 4 9. 16
10.(1) 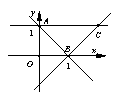 解析:已知实数
解析:已知实数![]() 、
、![]() 满足
满足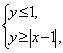 在坐标系中画出可行域,三个顶点分别是A(0,1),B(1,0),C(2,1),∴
在坐标系中画出可行域,三个顶点分别是A(0,1),B(1,0),C(2,1),∴ ![]() 的最大值是4.
的最大值是4.
(2)由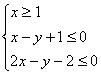 ,画出可行域,得交点A(1,2),B(3,4),则
,画出可行域,得交点A(1,2),B(3,4),则![]() 的最小值是5.
的最小值是5.
11.解若![]() 且
且![]() 所以
所以![]() ,
,
![]()
![]()
![]()
∴ ![]() ,则(
,则(![]() )≥
)≥![]()
12.解:令![]()
显然![]() 可以成立,当
可以成立,当![]() 时,
时,![]()
而![]() ,
,![]() 是方程
是方程![]() 的两个实数根
的两个实数根
所以![]() ,
,![]() 得出
得出![]() ,
,![]() .
.
C组题(共100分)
1.B 2.A 3.D 4.B 5D
6 . ![]()
![]()
![]()
![]()
7. ![]()
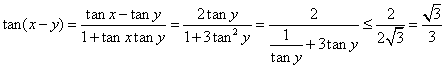
而![]() ,
,![]()
8. ![]()
![]()
9. f(x1)<f(x2)
10. 解:![]()
令![]() ,则
,则![]()
对称轴![]() ,而
,而![]()
![]() 是
是![]() 的递增区间,当
的递增区间,当![]() 时,
时,![]()
![]() .
.
11..解 (1)依题意,汽车从甲地匀速行驶到乙地所用时间为![]() ,
,
全程运输成本为y=a·![]() +bv2·
+bv2·![]() =s
=s![]()
∴所求函数及其定义域为y=s![]() v∈(0,c)
v∈(0,c)
(2)依题意知s、a、b、v均为正数 ∴y=s![]() ≥2s
≥2s![]()
当且仅当![]() =bv,即v=
=bv,即v=![]() 时,等号成立.
时,等号成立.
若![]() ≤c,则当v=
≤c,则当v=![]() 时,全程运输成本最小,最小值为2s
时,全程运输成本最小,最小值为2s![]() ;
;
若![]() >c,则当v∈(0,c)时,有
>c,则当v∈(0,c)时,有
s![]() ∵v∈(0,c)
∵v∈(0,c)
∴![]() 即a>bc2 ∴a-bcv>a-bc2>0∴s
即a>bc2 ∴a-bcv>a-bc2>0∴s![]()
当且仅当v=c时,等号成立,即当v=c时,全程运输成本最小,最小值为s![]() .
.
综上所述,为使全程运输成本最小,当![]() ≤c时,行驶速度应为v=
≤c时,行驶速度应为v=![]() km/h;当
km/h;当![]() >c时,行驶速度为c km/h.
>c时,行驶速度为c km/h.
点评 利用平均值不等式求函数的最大值和最小值时,应注意必须具备三个条件:①都是正数;②和或积是一个常数;③这两个或三个正数可以相等.这三个条件缺一不可,本题中由v=![]() 不一定是定义域内的值,故要讨论说明.
不一定是定义域内的值,故要讨论说明.
12、解:⑴![]() 不等式
不等式![]() <0的解集为
<0的解集为![]() ∴
∴![]() 得
得![]()
⑵![]() f(x)=
f(x)=![]() 在
在![]() 上递增,∴
上递增,∴![]()
又![]() ,
,
由![]() ,可知0<
,可知0<![]() <1
<1
由![]() , 得0<x<
, 得0<x<![]()
由![]() 得x<
得x<![]() 或x>1
或x>1
故原不等式的解集为![]() x0<x<
x0<x<![]() 或1<x<
或1<x<![]()
![]()