高一数学第一学期期中教学质量检测
高一级数学试卷
考试时间:100分钟,满分100分.
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.下列关系正确的是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知集合![]() ,
,![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列函数中,图象过定点![]() 的是
的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若![]() ,则
,则![]() 的值是:
的值是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数![]() 的零点所在的区间是
的零点所在的区间是
A.(0,1)
B.(1,2) C.(2,3) D.(3,+![]() )
)
6.已知函数![]() 是偶函数,则当
是偶函数,则当![]() 时,
时,![]() 的值域是:
的值域是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
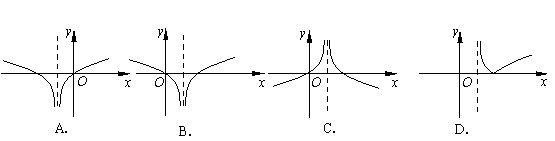 7.函数
7.函数![]() 的图像大致是
的图像大致是
8.某林场计划第一年造林10 000亩,以后每年比前一年多造林20%,则第四年造林
A.14400亩 B.172800亩 C.17280亩 D.20736亩
9.设![]() 均为正数,且
均为正数,且![]() ,
,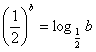 ,
,![]() .则
.则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知函数![]() (
(![]() ),对于任意的正实数
),对于任意的正实数![]() 下列等式成立的是
下列等式成立的是
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卷中的横线上.
11.若幂函数![]() 的图象过点
的图象过点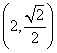 ,则
,则![]() _________
_________
12.函数![]() 的定义域是
的定义域是
13. 用二分法求函数![]() 在区间
在区间![]() 上零点的近似解,经验证有
上零点的近似解,经验证有![]() 。若给定精确度
。若给定精确度![]() ,取区间的中点
,取区间的中点![]() ,计算得
,计算得![]() ,则此时零点
,则此时零点![]() _____________(填区间)
_____________(填区间)
14.已知函数![]() ,有以下命题:1函数
,有以下命题:1函数![]() 的图象在y轴的一侧;2函数
的图象在y轴的一侧;2函数![]() 为奇函数;3函数
为奇函数;3函数![]() 为定义域上的增函数;4函数
为定义域上的增函数;4函数![]() 在定义域内有最大值,则正确的命题序号是 。
在定义域内有最大值,则正确的命题序号是 。
三、解答题:本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题8分)
已知集合![]()
![]() ,
,![]() ,
,
求:(1)![]() ;(2)
;(2)![]()
16.(本小题9分)已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)求函数![]() 的零点;
的零点;
(3)若函数f(x)的最小值为![]() ,求
,求![]() 的值。
的值。
17.(本小题9分)
已知函数![]() .
.
(1)求证:不论![]() 为何实数
为何实数![]() 总是为增函数;
总是为增函数;
(2)确定![]() 的值, 使
的值, 使![]() 为奇函数;
为奇函数;
(3)当![]() 为奇函数时, 求
为奇函数时, 求![]() 的值域.
的值域.
18. (本小题8分)
某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需要增加投入100元,已知总收益满足函数: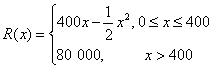 ,其中
,其中![]() 是仪器的月产量。
是仪器的月产量。
(1)将利润![]() 元表示为月产量
元表示为月产量![]() 台的函数;
台的函数;
(2)当月产量为何值时,公司所获得利润最大?最大利润是多少?(总收益=总成本+利润)
19.(本小题10分)
设函数![]() 定义在
定义在![]() 上,对于任意实数
上,对于任意实数![]() ,恒有
,恒有
![]() ,且当
,且当![]() 时,
时,![]()
(1)求证: ![]() 且当
且当![]() 时,
时,![]()
(2)求证: ![]() 在
在![]() 上是减函数;
上是减函数;
(3)设集合![]() ,
,![]() ,
,
且![]() , 求实数
, 求实数![]() 的取值范围。
的取值范围。