姓名_______班级_________
_______________号 高一数学三角函数测试(2008年3月)
撰稿： 方锦昌 电子邮箱 fangjingchang2 手机号码
一、选择题：(5×10=50′)
1、若 –π/2<a<0，则点
位于（
）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．若
，
则
的值是（ ）
A．
B．
C． 
D．
3、函数
在区间
的简图是（ ）
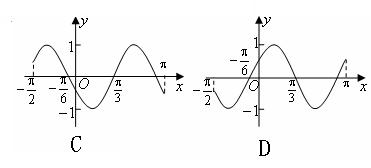
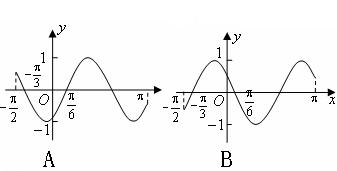
4．函数
的最小正周期是（ ）
A．
B．
C．
D．
5．满足函数
和
都是增函数的区间是（ ）
A．
, 
B．
,
C．
, D．
6．要得到函数
的图象，只需将函数
的图象（ ）
A．向右平移
个单位 B．向右平移
个单位 C．向左平移个单位 D．向左平移个单位
7．函数
的图象的一条对称轴方程是（ ）
A．
B．
C．
D．
8．函数y=cos2x –3cosx+2的最小值是（ ）
A．2 B．0 C．
D．6
9．如果
在第三象限，则
必定在第（ ）象限
A．一、二 B．一、三 C．三、四 D．二、四
10．已知函数
在同一周期内，当
时有最大值2，当x=0时有最小值-2，那么函数的解析式为（ ）
A．
B．
C．
D．
二、填空题：11．终边落在y轴上的角的集合是____________________
12、设
是某港口水的深度
（米）关于时间t（时）的函数，其中
．下表是
该港口某一天从0时至24时记录的时间t与水深y的关系：
| X | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| Y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察，函数的图象可以近似地看成函数
的图象.下面的函数中，最能近似表示表中数据间对应关系的函数有(填序号)________
(1)．
(2)．
(3)．
(4)．
13．函数
的定义域是___________________________
14．已知
，且x是第二、三象限角，则a的取值范围是________
15、函数
的图象为
，则如下结论中正确的序号是 _____ ①、图象关于直线
对称； ②、图象关于点
对称； ③、函数
在区间
内是增函数； ④、由
的图角向右平移
个单位长度可以得到图象．
三、解答题：16题．设
是角终边上不同于原点O的某一点，请求出角的正弦、余弦、和正切的三角函数之值.。
17题、 已知函数f(x)=Asin(ωx+j)的图象如图所示，试依图指出：
(1)、f(x)的最小正周期； (2、)使f(x)=0的x的取值集合； (3)、使f(x)＜0的x的取值集合；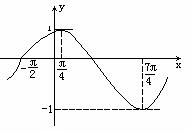 
(4)、f(x)的单调递增区间和递减区间；
(5)、求使f(x)取最小值的x的集合； (6)、图象的对称轴方程； (7)、图象的对称中心．
18题、化简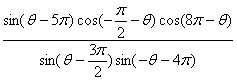
19题、已知
的最大值为
，最小值为
。求函数
的周期、最值，并求取得最值时的
之值；并判断其奇偶性。
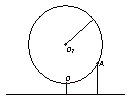20、如图，某大风车的半径为
，每
旋转一周，它的最低点
离地面
。风车圆周上一点
从最低点开始，运动
后与地面的距离为
。
⑴求函数
的关系式； ⑵画出函数的图象。
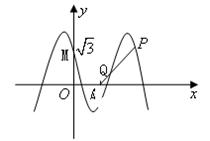21题、如图所示，函数
的图象与轴相交于点M
，且该函数的最小正周期为
．
（1）
求
和
的值； （2）已知点
，点
是该函数图象上一点，点
是
的中点，当
，
时，求
的值
参考答案：
一、选择题答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | A | A | C | D | A | A | B | D | C |
二、填空题答案：
11． 
12、 (1)．
13． 
14． 
15、 ①②③
三、解答题答案：
17题、 
18题、原式=-sinq
19题、a=;b=1
20题、y=2.5-2cos t (t≥0)
21题、解：（1）将
，
代入函数
中得
，
因为
，所以
．由已知
，且
，得
．
（2）因为点，是的中点，．所以点的坐标为
．
又因为点在
的图象上，且
，所以
，
，从而得
或
，即
或
．