夷陵中学高一数学培优资料
高一数学三角函数的综合应用测试
例1. 已知α、β为锐角,且x(α+β-![]() )>0,试证不等式f(x)=
)>0,试证不等式f(x)=![]() x<2对一切非零实数都成立
x<2对一切非零实数都成立![]()
证明![]() 若x>0,则α+β>
若x>0,则α+β>![]()
∵α、β为锐角,∴0<![]() -α<β<
-α<β<![]() ;0<
;0<![]() -β<
-β<![]() ,
,
∴0<sin(![]() -α)<sinβ
-α)<sinβ![]() 0<sin(
0<sin(![]() -β)<sinα,
-β)<sinα,
∴0<cosα<sinβ,0<cosβ<sinα,
∴0<![]() <1,0<
<1,0<![]() <1, ∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2
<1, ∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2![]()
若x<0,α+β<![]() ,∵α、β为锐角, 0<β<
,∵α、β为锐角, 0<β<![]() -α<
-α<![]() ,0<α<
,0<α<![]() -β<
-β<![]() ,
,
0<sinβ<sin(![]() -α), ∴sinβ<cosα,0<sinα<sin(
-α), ∴sinβ<cosα,0<sinα<sin(![]() -β),
-β),
∴sinα<cosβ,∴![]() >1,
>1, ![]() >1,
>1,
∵f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=2,∴结论成立![]()
例2、已知函数f(x)=tan(![]() sinx)
sinx)
(1)求f(x)的定义域值域;
(2)在(-π,π)中,和求f(x)的单调区间;
(3)判定方程f(x)=tan![]() π在区间(-π,π)上解的个数。
π在区间(-π,π)上解的个数。
解:(1)∵-1≤sinx≤1 ∴ - ![]() ≤
≤![]() sinx≤
sinx≤![]() 。又函数y=tanx在x=kπ+
。又函数y=tanx在x=kπ+![]() (k∈Z)处无定义,
(k∈Z)处无定义,
且 (-![]() ,
,![]() )
)![]() [-
[-![]() ,
,![]() ]
]![]() (-π, π),
(-π, π),
∴令![]() sinx=±
sinx=±![]() ,则sinx=±
,则sinx=±![]() 解之得:x=kπ±
解之得:x=kπ±![]() (k∈Z)
(k∈Z)
∴f(x)的定义域是A={xx∈R,且x≠kπ±![]() ,k∈Z}
,k∈Z}
∵tanx在(-![]() ,
,![]() )内的值域为(-∞,+∞),而当x∈A时,函数y=
)内的值域为(-∞,+∞),而当x∈A时,函数y=![]() sinx的值域B满足(-
sinx的值域B满足(-![]() ,
,![]() )
)![]() B ∴f(x)的值域是(-∞,+∞)。
B ∴f(x)的值域是(-∞,+∞)。
(2)由f(x)的定义域知,f(x)在[0,π]中的x=![]() 和x=
和x=![]() 处无定义。
处无定义。
设t=![]() sinx,则当x∈[0,
sinx,则当x∈[0, ![]() )∪(
)∪(![]() ,
,![]() )∪(
)∪(![]() ,π)时,t∈[0,
,π)时,t∈[0, ![]()
![]() ∪(
∪(![]() ,
,![]()
![]() ,且以t为自变量的函数y=tant在区间(0,
,且以t为自变量的函数y=tant在区间(0,![]() ),(
),(![]() ,
,![]()
![]() 上分别单调递增。
上分别单调递增。
又∵当x∈[0,![]() ]时,函数t=
]时,函数t=![]() sinx单调递增,且t∈[0,
sinx单调递增,且t∈[0, ![]()
![]()
当x∈(![]() ,
,![]()
![]() 时,函数t=
时,函数t=![]() sinx单调递增,且t∈(
sinx单调递增,且t∈(![]() ,
, ![]()
![]()
当x∈[![]() ,
,![]()
![]() 时,函数t=
时,函数t=![]() sinx单调递减,且t∈(
sinx单调递减,且t∈(![]() ,
, ![]()
![]()
当x∈(![]() ,π)时,函数t=
,π)时,函数t=![]() sinx单调递减,且t∈(0,
sinx单调递减,且t∈(0,![]() )
)
∴f(x)=tan(![]() sinx)在区间[0,
sinx)在区间[0,![]()
![]() ,(
,(![]() ,
,![]()
![]() 上分别是单调递增函数;在
上分别是单调递增函数;在![]() 上是单调递减函数。
上是单调递减函数。
又f(x)是奇函数,所以区间(-![]() ,0
,0![]() ,[-
,[-![]() ,-
,-![]()
![]() 也是f(x)的单调递增区间
也是f(x)的单调递增区间![]() 是f(x)的递减区间。
是f(x)的递减区间。
故在区间(-π,π)中,f(x)的单调递增区间为:[-![]() ,-
,-![]()
![]() ,(-
,(-![]() ,
,![]() ),(
),(![]() ,
,![]()
![]() 单调递减区间为
单调递减区间为![]() 。
。
(3)由f(x)=tan![]() π得:tan(
π得:tan(![]() sinx)=tan(
sinx)=tan(![]() π)
π)![]()
![]() sinx=kπ+
sinx=kπ+![]() π (k∈Z)
π (k∈Z)
![]() sinx=k
sinx=k![]() +
+![]() (k∈Z)①
(k∈Z)①
又∵-1≤sinx≤1,∴![]() ∴k=0或k= -1
∴k=0或k= -1
当k=0时,从①得方程sinx=![]() 当k=1时,从①得方程sinx= -
当k=1时,从①得方程sinx= -![]() +
+![]()
显然方程sinx=![]() ,sinx= -
,sinx= -![]() +
+![]() ,在(-π, π)上各有2个解,故f(x)=tan
,在(-π, π)上各有2个解,故f(x)=tan![]() π在区间(-π,π)上共有4个解。
π在区间(-π,π)上共有4个解。
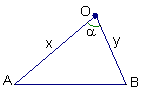
例3.(2004年全国卷Ⅱ)已知锐角三角形ABC中,![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)设AB=3,求AB边上的高.
(Ⅰ)证明:![]()
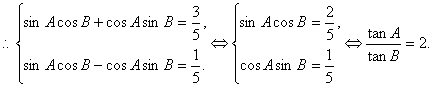
所以![]()
(Ⅱ)解:![]() ,
,![]()
即![]() ,将
,将![]() 代入上式并整理得
代入上式并整理得
![]() 解得
解得![]() ,舍去负值得
,舍去负值得![]() ,
,![]() 设AB边上的高为CD.则AB=AD+DB=
设AB边上的高为CD.则AB=AD+DB=![]() 由AB=3,得CD=2+
由AB=3,得CD=2+![]() . 所以AB边上的高2+
. 所以AB边上的高2+![]() .
.
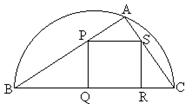 例4. 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=
例4. 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]() .
.
解:(1)![]()
设正方形边长为![]() ,则
,则![]()
![]()
![]()
(2)当![]() 固定,
固定,![]() 变化时,
变化时,![]()
令![]()
![]() ,用导数知识可以证明:函数
,用导数知识可以证明:函数![]() 在
在![]() 是减函数,于是当
是减函数,于是当![]() 时,
时,![]() 取最小值,此时
取最小值,此时![]() 。
。
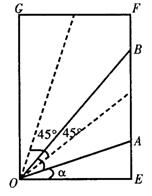 例5、如图,A、B是一矩形 OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=
例5、如图,A、B是一矩形 OEFG边界上不同的两点,且∠AOB=45°,OE=1,EF=![]() ,设∠AOE=α.
,设∠AOE=α.
(1)写出△AOB的面积关于α的函数关系式f(α);
(2)写出函数f(x)的取值范围。
当k=1时,从①得方程sinx= -![]() +
+![]()
当k=1时,从①得方程sinx= -![]() +
+![]()
解:(1)∵OE=1,EF=![]()
∴∠EOF=60°
当α∈[0,15°]时,△AOB的两顶点A、B在E、F上,且AE=tanα,BE=tan(45°+α)
∴f(α)=S△AOB=![]() [tan(45°+α)-tanα]
[tan(45°+α)-tanα]
=![]() =
=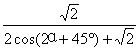
当a∈(15°,45°]时,A点在EF上,B点在FG上,且OA=![]() ,OB=
,OB=![]()
∴![]() =S△AOB=
=S△AOB=![]() OA·OB·sin45°=
OA·OB·sin45°=![]() ·
·![]() ·sin45°=
·sin45°=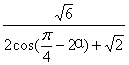
综上得:f(α)= 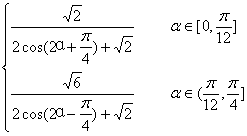
(2)由(1)得:当α∈[0,![]() ]时
]时
f(α)= 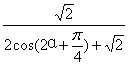 ∈[
∈[![]() ,
,![]() -1]
-1]
且当α=0时,f(α)min=![]() ;α=
;α=![]() 时,f(α)max=
时,f(α)max=![]() -1;
-1;
当α∈![]() 时,-
时,-![]() ≤2α-
≤2α-![]() ≤
≤![]() ,f(α)=
,f(α)=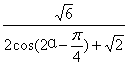 ∈[
∈[![]() -
-![]() ,
,![]() ]
]
且当α=![]() 时,f(α) min=
时,f(α) min=![]() -
-![]() ;当α=
;当α=![]() 时,f(α) max=
时,f(α) max=![]() 所以f(x) ∈[
所以f(x) ∈[![]() ,
,![]() ]。
]。
巩固练习![]()
1![]() 函数y=-x·cosx的部分图象是( )
函数y=-x·cosx的部分图象是( )
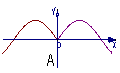
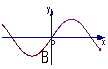
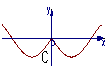
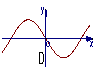
2![]() 函数f(x)=cos2x+sin(
函数f(x)=cos2x+sin(![]() +x)是( )
+x)是( )
A![]() 非奇非偶函数 B
非奇非偶函数 B![]() 仅有最小值的奇函数
仅有最小值的奇函数
C![]() 仅有最大值的偶函数 D
仅有最大值的偶函数 D![]() 既有最大值又有最小值的偶函数
既有最大值又有最小值的偶函数
3![]() 函数f(x)=(
函数f(x)=(![]() )|cosx|在[-π,π]上的单调减区间为_________
)|cosx|在[-π,π]上的单调减区间为_________![]()
4![]() 设ω>0,若函数f(x)=2sinωx在[-
设ω>0,若函数f(x)=2sinωx在[-![]() ,]上单调递增,则ω的取值范围是_________
,]上单调递增,则ω的取值范围是_________![]()
5![]() 设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0
设二次函数f(x)=x2+bx+c(b,c∈R),已知不论α、β为何实数恒有f(sinα)≥0和f(2+cosβ)≤0![]()
(1)求证![]() b+c=-1;
b+c=-1;
(2)求证c≥3;
(3)若函数f(sinα)的最大值为8,求b,c的值![]()
6![]() 有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问
有一块半径为R,中心角为45°的扇形铁皮材料,为了获取面积最大的矩形铁皮,工人师傅常让矩形的一边在扇形的半径上,然后作其最大内接矩形,试问![]() 工人师傅是怎样选择矩形的四点的?并求出最大面积值
工人师傅是怎样选择矩形的四点的?并求出最大面积值![]()
7![]() 设-
设-![]() ≤x≤
≤x≤![]() ,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值
,求函数y=log2(1+sinx)+log2(1-sinx)的最大值和最小值![]()
8![]() 是否存在实数a,使得函数y=sin2x+a·cosx+
是否存在实数a,使得函数y=sin2x+a·cosx+![]() a-
a-![]() 在闭区间[0,
在闭区间[0,![]() ]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由
]上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由![]()
参考答案![]()
1![]() 解析
解析![]() 函数y=-xcosx是奇函数,图象不可能是A和C,又当x∈(0,
函数y=-xcosx是奇函数,图象不可能是A和C,又当x∈(0, ![]() )时,y<0
)时,y<0![]()
答案![]() D
D
2![]() 解析
解析![]() f(x)=cos2x+sin(
f(x)=cos2x+sin(![]() +x)=2cos2x-1+cosx=2[(cosx+
+x)=2cos2x-1+cosx=2[(cosx+![]() ]-1
]-1![]() 答案
答案![]() D
D
3![]() 解
解![]() 在[-π,π]上,y=|cosx|的单调递增区间是[-
在[-π,π]上,y=|cosx|的单调递增区间是[-![]() ,0]及[
,0]及[![]() ,π]
,π]![]() 而f(x)依|cosx|取值的递增而递减,故[-
而f(x)依|cosx|取值的递增而递减,故[-![]() ,0]及[
,0]及[![]() ,π]为f(x)的递减区间
,π]为f(x)的递减区间![]()
4![]() 解
解![]() 由-
由-![]() ≤ωx≤
≤ωx≤![]() ,得f(x)的递增区间为[-
,得f(x)的递增区间为[-![]() ,
,![]() ],由题设得
],由题设得
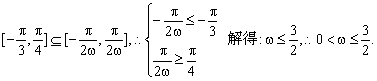
5![]() 解
解![]() (1)∵-1≤sinα≤1且f(sinα)≥0恒成立,∴f(1)≥0
(1)∵-1≤sinα≤1且f(sinα)≥0恒成立,∴f(1)≥0
∵1≤2+cosβ≤3,且f(2+cosβ)≤0恒成立![]() ∴f(1)≤0
∴f(1)≤0![]()
从而知f(1)=0∴b+c+1=0![]()
(2)由f(2+cosβ)≤0,知f(3)≤0,∴9+3b+c≤0![]() 又因为b+c=-1,∴c≥3
又因为b+c=-1,∴c≥3![]()
(3)∵f(sinα)=sin2α+(-1-c)sinα+c=(sinα-![]() )2+c-(
)2+c-(![]() )2,
)2,
 当sinα=-1时,[f(sinα)]max=8,由
当sinα=-1时,[f(sinα)]max=8,由![]() 解得b=-4,c=3
解得b=-4,c=3![]()
6![]()
 解
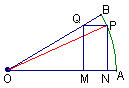
解![]() 如下图,扇形AOB的内接矩形是MNPQ,连OP,则OP=R,设∠AOP=θ,则∠QOP=45°-θ,NP=Rsinθ,在△PQO中,
如下图,扇形AOB的内接矩形是MNPQ,连OP,则OP=R,设∠AOP=θ,则∠QOP=45°-θ,NP=Rsinθ,在△PQO中,![]() ,
,
∴PQ=![]() Rsin(45°-θ)
Rsin(45°-θ)![]()
S矩形MNPQ=QP·NP=![]() R2sinθsin(45°-θ)
R2sinθsin(45°-θ)
=![]() R2·[cos(2θ-45°)-
R2·[cos(2θ-45°)-![]() ]≤
]≤![]() R2,
R2,
当且仅当cos(2θ-45°)=1,即θ=22![]() 5°时,S矩形MNPQ的值最大且最大值为
5°时,S矩形MNPQ的值最大且最大值为![]() R2
R2![]()
工人师傅是这样选点的,记扇形为AOB,以扇形一半径OA为一边,在扇形上作角AOP且使∠AOP=22![]() 5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为
5°,P为边与扇形弧的交点,自P作PN⊥OA于N,PQ∥OA交OB于Q,并作OM⊥OA于M,则矩形MNPQ为面积最大的矩形,面积最大值为![]() R2
R2![]()
7![]() 解
解![]() ∵在[-
∵在[-![]() ]上,1+sinx>0和1-sinx>0恒成立,
]上,1+sinx>0和1-sinx>0恒成立,
∴原函数可化为y=log2(1-sin2x)=log2cos2x,
又cosx>0在[-![]() ]上恒成立,
]上恒成立,
∴原函数即是y=2log2cosx,在x∈[-![]() ]上,
]上,![]() ≤cosx≤1
≤cosx≤1![]()
∴log2![]() ≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-
≤log2cosx≤log21,即-1≤y≤0,也就是在x∈[-![]() ]上,ymax=0, ymin=-1
]上,ymax=0, ymin=-1![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
综合上述知,存在![]() 符合题设
符合题设![]()