高一集合不等式的解法函数测试题
命题人：杨昌座
1．设集合P={3，4，5}，Q={4，5，6，7}，定义P·Q={(a,b) ｜a∈P,b∈Q},则P·Q中元素的个数为（ ）D
A. 3 B. 7 C.10 D.12
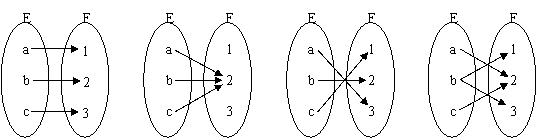2．在下列集合E到集合F的对应中，不能构成E到F的映射是（ D ）
A B C D
3．已知集合A＝{1，a2}，实数a不能取的值的集合是（A ）
A．{－1，1} B．{－1} C．{－1，0，1} D．{1}
4．右图中阴影部分所对应的集合是（ C ）
A. (CUA)ÇB B. CU(AÈB) C. (CUB)ÇA D. CU(AÇB)
5．下列各组函数中，表示同一个函数的是：（ D ）
A、y=x-1和
B、y=x0和y=1
C、f(x)=x2 和g(x)=(x+1)2
D、
和
6．设集合
，集合
＝正实数集，则从集合
到集合的映射只可能是（ C ）
A．
B．
C．
D．
7．下列函数中，在区间(0，＋∞)上是减函数的是（ D ）．
A．y＝－ B．y＝x C．y＝x2 D．y＝1－x
8．设全集是实数集
，
，且
，则实数
的
取值范围为（ C ）
A． 
B．
C． 
D． 
9．设函数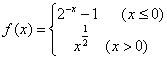
,若f(x0)>1，则x0的取值范围是（ D
）
A、（-1，1） B、（-1，+∞） C、（-∞，-2） D、（-∞，-1）∪（1，+∞）
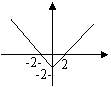
10．设函数y=f(x)的图像如图所示，则f(x)的解析式为（ A ）
A、y=x-2 B、y=x-2 C、y=-x+2 D、y=x+2
11．国内快递1000g以内的包裹的邮资标准如下表：
| 运送距离x (km) | 0＜x≤500 | 500＜x≤1000 | 1000＜x≤1500 | 1500＜x≤2000 | … |
| 邮资y (元） | 5.00 | 6.00 | 7.00 | 8.00 | … |
如果某人在南京要快递800g的包裹到距南京1200km的某地，那么他应付的邮资是( C )．
A．5.00元 B．6.00元 C．7.00元 D．8.00元
12．已知定义在区间[0，1]上的函数y=f(x),图象如图所示，对满足0<x1〈x2<1的任意x1,,
x2给出下列结论：C
①
|
②
|
xf(x)>xf(x);
③
<f(
).
|
|
|
A.0个 B.1个 C.2 个 D.3个
13．函数
的定义域为＿＿＿
＿＿＿＿＿；
14．定义f (x, y)=(y2, 2y-x)，若f (m, n)=(1,2)，则 (m,n)= （0，1）或（-4，-1）
15．函数f（x）＝
的递增区间是
。
16．已知函数f(x)满足：(1)对任意x1<x2，总有f(x1)<f(x2)；(2)对x1、x2
R，都有f(x1·x2)＝f(x1)·f(x2)；(3)函数f(x)的图象不是直线。写出一个同时满足上述三个条件的函数解析式 y＝x3(x
) .
17．已知全集U={1，2，3，4，5，6，7，8}，A={x1≤x≤5，x∈Z}，B={x2<x<9,x∈Z}。
（1） 求A∩B;
（2） 求（CUA）∪(CUB)。（10分）
解：（1）A∩B={3，4，5}
（2）（CUA）∪(CUB)= CU（A∩B）={1，2，6，7，8}
18．求下列函数的值域：
（1）
（2）
。
1．配方得
。
，
，
。从而函数的值域为
。
2．原函数的定义域是
。令
，则
，
。
。问题转化为求
值域的问题。
，
，
。从而函数的值域为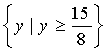
。
19．设函数f(x)=x2-2x-3 (1)求函数f(x)的零点；（2）画出函数图像，并写出单调区间。
解：（1）f(x)=x2-2x-3=0，x=3或x=-1 ∴函数f(x)的零点为x=3或x=-1；
（2）对称轴：x=1 单增区间：[-1，1]，
单减区间：
，[1，3]
20．某旅游公司有客房300间，每间房租为200元，每天客满，公司欲提高档次，并提高租金。如果每间客房每日增加20元，客房出租就减少10间，若不考虑其他因素，公司将房租提高到多少时，每天客房的租金总收入最高？（10分）
解：设公司将房租提高x个20元，则每天客房的租金收入y为：
y=(200+20x)(300-10x) （x∈N）
=60000+4000x-200x2
这个二次函数图像的对称轴为：
200+20x=200+20×10=400
当x=10时，y最大值=80000.
答：将房租提高到400元/间时，客房的租金总收入最高，每天为80000元。
21．已知函数
在区间
上为增函数，求a的取值范围。
解：令g(x)=x2-ax-a
∵f(x)=logag(x)在上为增函数，∴g(x)应在上为减函数
且g(x)>0在上恒成立
因此：
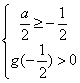即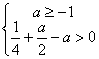
解得：
故实数a的取值范围是：
22．设定义在R上的函数f (x)，满足当x＞0时，f(x) ＞1且对任意的x,y ∈R都有f(x+y)=f(x) ·f(y),f(1)=2
（1）求f(0)
(2) 求证：对任意的x∈R,都有f(x)>0;
(3) 解不等式：f(3x-x2) ＞4
（1）f(x)=f(x+0)=f(x)f(0).故f(0) ≠0. 
x>0时,f(x)>1,又f(0)= [f(0)]2
f(0)=1
(2)f(x)=f(
+)=[f()]2≥0.假设存在某个x0R,使f(x0)=0,则对任意x>0，有f(x)=f[(x-x0)+x0]=
f(x-x0)f(x0)=0,与已知矛盾，xR均满足f(x)>0
(3)任取x1, x2R且x1< x2, 则x2-x1>0,故f(x2-x1)>1. f(x2)-f(x1)=
f[(x2-x1)+x1]-f(x1, )= f(x2-x1)
f(x1)- f(x1)= f(x1) f[(x2-x1)-1]>0,
xR时, f(x)为单调递增函数。 f(1)=2，则f(2)= f(1) f(1)=4。f(3x-x2)>4= f(2), 3x-x2>2,即1〈x<2.
不等式的解集为{x1〈x<2.}