高中数学学业评价试卷双向细目表必修1
| 考试内容 | A | B | C | |
| 集合 | 子集 | Ö | ||
| 交集与并集 | Ö | |||
| 补集 | Ö | |||
| 函数 | 映射与函数的概念 | Ö | ||
| 函数的定义域 | Ö | |||
| 函数的值域 | Ö | |||
| 函数的表示方法 | Ö | |||
| 函数的图象 | Ö | |||
| 函数的单调性 | Ö | |||
| 函数的奇偶性 | Ö | |||
| 指数函数 | Ö | Ö | ||
| 指数与对数 | Ö | |||
| 换底公式 | Ö | |||
| 对数函数 | Ö | |||
| 函数图象变换 | Ö | |||
| 幂函数 | Ö | |||
| 函数与方程 | Ö | |||
| 函数模型及其应用 | Ö |
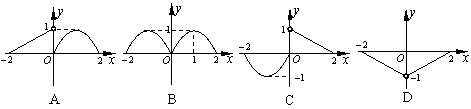
说明：A：了解 B：理解与掌握 C：综合运用
南京市高中数学学业评价试卷必修1(C卷)
一、选择题（每小题6分，共60分）
1．已知集合A＝｛x≤x＜｝和m＝π，则下列关系中正确的是( )．
A．mÍA B．mA C．｛m｝∈A D．｛m｝ÍA
2．若全集U＝{1，2，3，4}，集合A＝{1，2}，则满足A∪B＝U的集合B是( )．
A．1个 B．2个 C．3个 D．4个
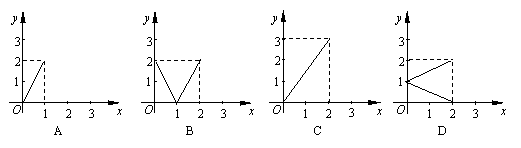3．设集合M＝{x0≤x≤2}，集合N＝{y0≤y≤2}，下图给出4个图形分别表示集合M到集合N的对应，其中是从集合M到集合N的函数的是( )．
4．已知函数y＝x2＋ax＋3的定义域为[－1，1]且当x＝－1时，函数有最小值；当x＝1时，函数有最大值，则a满足( )．
A．0＜a≤2 B．a≥2 C．a＜0 D．a∈R
5．当x∈[－2，2)时，f(x)＝3－x的值域是( )．
A．[，9） B．（，9） C．[，9] D．（，9]
6．已知指数函数y＝ax(a＞0且a≠1)在
0，
上的最大值与最小值的和为3，则实数a的值为( )．
A． B． C．2 D．4
7．函数y＝x2的图象与函数y＝的图象在第一象限的部分( )．
A．关于原点对称 B．关于x轴对称 C．关于y轴对称 D．关于直线y＝x对称
8．设0＜a＜1，则函数y＝loga(x＋5)的图象经过( )．
A．第二象限，第三象限，第四象限 B．第一象限，第三象限，第四象限
C．第一象限，第二象限，第四象限 D．第一象限，第二象限，第三象限
9．若关于x的方程ax＝x＋a有两个解，则实数a的取值范围是( )．
A．(1，＋∞)
B．(0，＋∞) C． (0，1) D．Æ
10．已知函数y＝f(x)的图象如右图所示，则函数y＝f(x)的图象为( )．
二、填空题（每小题5分，共30分）
11．设全集U＝｛2，3，a2＋2a－3｝，A＝｛2a－1，2｝，
UA＝｛5｝，则实数a的值为____________．
12．若集合A＝{xkx2＋4x＋4＝0}中只有一个元素，则实数k的值为__________．
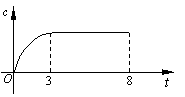13．某工厂8年来某种产品的总产量c与时间t (年)的函数关系如下图，下列四种说法：
（1）前三年，总产量增长的速度越来越快；
（2）前三年中，总产量增长的速度越来越慢；
（3）第三年后，这种产品停止生产；
（4）第三年后，年产量保持不变．
其中说法正确的是_______________．
14．若f(x)是R上的奇函数，当x＞0时，f(x)＝x(x＋1)，则当x＜0时，f(x)＝ ．
15．若log37·log29·log49a＝log4，则a的值为_____________．
16．若函数y＝的定义域为R，则实数m的取值范围是 ．
三、解答题（每小题14分，共70分）
17．（本题满分14分）已知≤x≤8，求函数f(x)＝(log2)(log2)的最大值和最小值．
18．（本题满分14分）已知函数f(x)＝x(1－)．
（1）判断f(x)的奇偶性；
（2）证明：当x≠0时，f(x)＞0．
19．（本题满分14分）设集合A＝｛xx2＋4x＝0｝，B＝｛xx2＋2(a＋1)x＋a2－1＝0｝．
(1)若A∪B＝B，求实数a的取值范围；
(2)若A∩B＝B，求实数a的取值范围．
20．（本题满分14分）设函数f(x)＝x2－4x－5．
(1)在区间[－2，6]上画出函数f(x)的图象；
(2)设集合A＝{xf(x)≥5}，B＝(－∞,－2]∪[0，4]∪[6 ，＋∞)，根据图象判断集合
和
之间的关系．
21．（本题满分14分）已知实数a＜０，函数f(x)＝a＋＋．
(1)设t＝＋，求t的取值范围；
(2)将f(x)表示为t的函数h(t)；
(3)若函数f(x)的最大值为g(a)，求g(a)．
必修1(C)
一、选择题（每小题6分，共60分）
1．D 2．D 3．B 4．B 5．D 6．C 7．D 8．A 9．A 10．B
二、填空题（每小题5分，共30分）
11．2 12．０或1 13．②④ 14．－x2＋x 15． 16．[，＋∞)
三、解答题（每小题14分，共70分）
17．解：由≤x≤8得≤log2x≤3，y＝( log2x－1)(2－log2x)＝－(log2x－)2＋．
当log2x＝时，即x＝2时，y取最大值；当log2x＝3时，即x＝8时，y取最小值－2．
18．解：（1）函数f(x)＝x(1－)=x()，所以f(－x)＝(－x)()＝x()，所以
f(x)是偶函数．
（2）当x＞0时，2x＞1，所以f(x)＝x()＞0，又因为f（x）是偶函数，所以当x＜0时，f(x)＝f(－x)＞0，于是，当x≠0时，f(x)＞0．
19．解：（1）A＝｛0，－4｝．又因为A∪B＝B，所以AÍB．
又B为一元二次方程的解集，最多有两个元素，因此B＝A＝｛0，－4｝．
即 解得a＝1．
所以若A∪B＝B时，实数a的取值范围是｛a a＝1｝．
（2）A∩B＝B即BÍA，则B可能为Æ，｛0｝，｛－4｝，｛0，－4｝．
当B＝Æ时，由△＝[2(a＋1)]2－4(a2－1)＜0，解得a＜－1；
当B＝｛0｝时，则解得a＝－1；
当B＝｛－4｝时，则无解；
当B＝｛0，－4｝时，由（1）得a＝1．
综上，A∩B＝B时，实数a的取值范围是｛a a≤－1或a＝1｝．
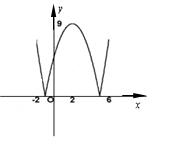
20．解：（1）如右图所示．
（2）方程f(x)＝5的解分别是2－，0，4和2＋，
由于f(x)在(－∞,－1］和[2，5]上单调递减，
在[－1，2]和[5，＋∞)上单调递增，
因此A＝(－∞,2－]∪[０，4]∪[2＋ ，＋∞)．
由所以B⊆A．
21．解：(1)令t＝＋．
要使有t意义，必须1＋x≥0且1－x≥0，即－1≤x≤1，
∴t2＝2＋2．∴t2∈[2，4]且t≥0 ．t的取值范围是[，2]．
(2)∵t2＝2＋2，∴＝t2－1．∴m(t)＝a(t2－1)＋t＝at2＋t－a，t∈[，2]．
(3) h(t)＝a(t2－1)＋t＝at2＋t－a，t∈[，2]．
∵a＜0，∴函数y＝h(t)， t∈ [，2]的图象是开口向下的抛物线的一段．
h(t)＝at2＋t－a＝a(t＋)2－a－．
若－∈[0，]时，即a≤－，则g(a)＝h()＝；
若－∈(，2]时，即－＜a≤－，则g(a)＝h(－)＝－a－；
若－∈(2，＋∞)时，即－＜a＜0，则g(a)＝h(2)＝a＋2．
综上有g(a)＝