高一12月份月考数学试题
第I卷(选择题,共60分)
一、选择题(本大题有12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将正确答案填涂在机读卡上).
1.设集合![]() 为
( )
为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() .
.
2. 使不等式![]() 成立的一个充分不必要条件是
( )
成立的一个充分不必要条件是
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 设等比数列的前n项积为![]() , 若
, 若![]() ,则一定有
( )
,则一定有
( )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D. ![]() .
.
4. 设![]() 且
且![]() ,
,![]() ,则M与N的大小关系是(
)
,则M与N的大小关系是(
)
A. ![]() B.
B. ![]() C.
C.
![]() D. 不能确定.
D. 不能确定.
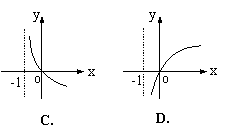
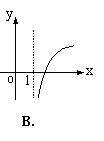
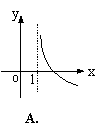 5. 若函数
5. 若函数![]() (
(![]() 且
且![]() )为增函数,则函数
)为增函数,则函数![]() 的大致图象是( )
的大致图象是( )
6.已知向量![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() .
.
7.设函数![]() ,当
,当![]() 时,
时,![]() 单调递增,则实数a的范围是( )
单调递增,则实数a的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() .
.
8. 设函数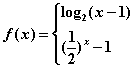
![]() , 若
, 若![]() ,则
,则![]() 的取值范围为 ( )
的取值范围为 ( )
A. ![]() B. (0,2) C.
B. (0,2) C.
![]() D.
D. ![]() .
.
9.给定两个向量![]() 实数
实数![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.3 D.
C.3 D.![]() .
.
10.将函数![]() 的图象按向量
的图象按向量![]() 平移后图象的解析式为
平移后图象的解析式为![]() ,则函数
,则函数![]() 的解析式可以是( )
的解析式可以是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() .
.
11.函数![]() 是 ( )
是 ( )
A. 周期为![]() 的奇函数 B. 周期为
的奇函数 B. 周期为![]() 的偶函数
的偶函数
C. 周期为![]() 的奇函数 D. 周期为
的奇函数 D. 周期为![]() 的偶函数.
的偶函数.
12.已知命题P:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;命题Q:
;命题Q:![]() 是减函数,若P或Q为真命题,P且Q为假命题,则实数
是减函数,若P或Q为真命题,P且Q为假命题,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() .
.
第II卷 (非选择题,共90分)
二、填空题(本大题有4个小题,每小题4分,共16分![]() 请把答案填在答题卷上相应的位置).
请把答案填在答题卷上相应的位置).
13. 设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() =____.
=____.
14. 函数![]() 的反函数
的反函数![]() ________.
________.
15. 已知向量![]() 的最大、最小值分别为m、n,则
的最大、最小值分别为m、n,则![]() __________.
__________.
16. 已知不等式![]() 的解集为
的解集为![]() ,则不等式
,则不等式![]() 的解集为____________.
的解集为____________.
三、解答题(本大题有6个小题,共74分。解答应写出必要的文字说明、证明过程或演算步骤).
17. (本小题满分13分)已知向量![]() 、
、![]() 满足:
满足:![]() ,其中
,其中![]() .
.
(1) 用![]() 表示
表示![]() ;
;
(2) 当![]() 最小时,求
最小时,求![]() 与
与![]() 的夹角θ的大小.
的夹角θ的大小.
18. (本小题满分13分)设函数![]() 的图象与函数
的图象与函数![]() 的图象关于原点对称,且
的图象关于原点对称,且![]() .
.
(1) 求函数![]() 的解析式;
(2) 解关于x的不等式:
的解析式;
(2) 解关于x的不等式:![]() .
.
19. (本小题满分12分) 已知函数![]()
(1) 若![]() 的单调递增区间;
的单调递增区间;
(2) 若![]() 的最大值为4,求a的值,并求出这时x的值.
的最大值为4,求a的值,并求出这时x的值.
20. (本小题满分12分) 设![]() 是正项数列
是正项数列![]() 的前n项和,且
的前n项和,且![]() .
.
(1) 求![]() 的值;
的值;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) ![]()
![]() 的值.
的值.
21. (本小题满分12分) 在![]() 中,已知角A为锐角,角A、B、C的对边分别为a、b、c,
中,已知角A为锐角,角A、B、C的对边分别为a、b、c,![]() .
.
(1) 求![]() 的值;
的值;
(2) 若![]() ,
,![]() ,求
,求![]() 的值.
的值.
22. (本小题满分12分) 已知函数![]() 对任意的实数m、n都有:
对任意的实数m、n都有:![]() ,且当
,且当![]() 时,有
时,有![]() .
.
(1)求证:![]() 在R上为增函数;
在R上为增函数;
(2)若![]() ,解关于x的不等式
,解关于x的不等式![]() ;
;
(3)若关于x的不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
一、选择题:1. B 2 .C 3.B 4.A 5.D 6.B 7 .C 8.C 9.A 10.B 11.C 12.B
二、填空题:
13. ![]() 14.
14.![]() 15.2
16.
15.2
16.![]()
三、解答题:
17(本题满分13分)(1)由已知有: ![]()
![]()
∴ ![]()
(2)![]()
此时![]()
∴ ![]() ∴
∴ ![]()
18. (本题满分13分)(1)在![]() 上任取一点
上任取一点![]() ,它关于原点对称点为
,它关于原点对称点为![]() , 则
, 则![]() 在
在![]() 上
上
∴![]() 即
即![]()
∴ ![]()
(2)不等式即:![]()
∴![]() 即
即 ![]()
∴![]() 或
或 ![]()
∴ ![]() 或
或![]()
∴ 不等式解集为 ![]()
19. (本题满分12分)(1)![]()
![]()
当![]()
即![]() 时,
时,![]() 为增函数
为增函数
(2)当![]() 时,
时,![]()
![]() ,
,
![]()
![]()
![]()
当![]() 时,
时,![]()
即![]()
又![]()
![]()
20. (本题满分12分)⑴ 当n = 1时,![]()
解出a1 = 3
⑵ 又4sn = an2 + 2an-3 ①
4sn-1 = ![]() + 2an-3 (n≥2) ②
+ 2an-3 (n≥2) ②
①-② 4an = an2-![]() + 2an-2an-1
+ 2an-2an-1
即![]()
∴ ![]()
![]() (
(![]() )
)
![]() 是以3为首项,2为公差之等差数列
是以3为首项,2为公差之等差数列
![]()
⑶ ![]() ③
③
又![]() ④
④
④-③ ![]()
![]()
![]()
∴![]()
21. (本题满分12分)⑴在△ABC中,因为角A为锐角且 ![]() ,
,
所以![]()
![]()
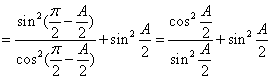
![]()
⑵由![]()
![]() ,得
,得![]() ①
①
由余弦定理,![]() ,即
,即![]() ②
②
由①②解得![]() 或
或![]()
22. (本题满分12分)
(1)
证:任取![]() 且
且![]() ,∴
,∴![]() ,
,![]()
∵![]()
∴![]()
∴![]() 在R上为增函数
在R上为增函数
(2)∵![]()
∴![]()
∴![]() 即
即![]()
∵![]() 在R上为增函数
在R上为增函数
∴![]()
∴![]()
(3)令![]()
∴![]()
∴![]()
∵![]() 即
即 ![]()
∴![]()
由①知 ![]() 恒成立
恒成立
∴![]() 恒成立
恒成立
∴![]()
∴![]()