三、函数思想方法的应用
【要点】
1．函数的思想，是指运用运动变化的观点，分析和研究数量关系，通过建立或构造函数关系式，运用函数的图像和性质去分析问题、转化问题，从而使问题获得解决的思想方法．
2．方程的思想，是指根据数学问题中变量间的特殊关系，有意识地构造方程或方程组，通过解方程或方程组，或者运用方程的性质去分析、转化问题，使问题获得解决的思想方法．
3．函数和方程是密切相关的，可以互相转化。比如研究函数y=f(x)与y=g(x)的图象的交点问题，就是研究方程f(x)=g(x)的实数解的问题；解方程f(x)=0，就是求函数y=f(x)的零点．
4．函数应用题的解题步骤简述如下：
（1）审题：阅读理解文字表达的题意,分清条件和结论；
（2）建模：将文字语言转化为数学语言,利用数学知识,建立相应的数学模型,；
（3）求模：求解数学模型，得到数学结论；
（4）作答：对结果进行验证或评估，作出解释或回答。
解应用题可归结为“过三关”：一是事理关，即读懂题意，需要一定的阅读理解能力；二是文理关，即把文字语言转化为数学的符号语言；三是数理关，即构建相应的数学模型，构建之后还需要扎实的基础知识和较强的数理能力。
【例题】
1．方程x2=2x的解的个数为（ ）
A．0 B．1 C．2 D．3
2．已知
，（a、b、c∈R），则有（
）
A．
B．
C．
D．
3．已知关于
的方程 
－(2 m－8)x +
－16 = 0的两个实根 
、
满足 ＜
＜，则实数m的取值范围_______________．
4．关于x的方程x2－4x+3－a=0有三个不相等的实数根，则实数a的值是______．
5．若不等式
≥
x+11-a的解集为{x-4≤x≤-2}，求实数a的值．
6．已知直线y=3-x和坐标轴交于A、B两点，若抛物线y=-x2+mx-1和线段AB有两个不同的交点，求实数m的范围．
7．设不等式2x－1>m（x
－1）对满足m≤2的一切实数m的取值都成立．求x的取值范围．
8．设f（x）＝lg
，如果当x∈（-∞,1]时f（x）有意义，求实数a的取值范围．
9．若方程lg（－x＋3x－m）＝lg（3－x）在x∈（0,3）内有唯一解，求实数m的取值范围．
10．已知函数f(x)=logm
(1)若f(x)的定义域为［α，β］，（β＞α＞0），判断f(x)在定义域上的增减性，并加以说明；
(2)当0＜m＜1时，使f(x)的值域为［logm［m(β–1)］，logm［m(α–1)］］的定义域区间为［α,β］(β＞α＞0)是否存在？请说明理由．
11．（1997年全国高考题）甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米／时，已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度 v（千米／时）的平方成正比，比例系数为b；固定部分为a元．
（1）把全程运输成本y（元）表示为速度v（千米／时）的函数，并指出函数的定义域；
（2）为了使全程运输成本最小，汽车应以多大速度行驶？
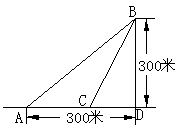
12．某海滨浴场的岸边可以近似的看成直线，位于岸边A处的救生员发现海中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D处，然后游向B处，若救生员在岸边的行进速度为6米/秒，在海中的行进速度2米/秒
（1）分析救生员的选择是否正确；
（2）在AD上找一落点C，使救生员从A到B的时间最短，并求出最短时间。
【习题】
一、选择题（A、B、C三级试题分别为3、2、1，共6小题）：
1.
方程2
＝x＋2x＋1的实数解的个数是_____．
A．1 B．2 C．3 D．以上都不对
2. 方程lgx+x=3的解所在区间为（ C ）
A．(0，1) B．(1，2) C．(2，3) D．(3，+∞)
3.
函数
的最小值是
A．1 B．2 C．25/12 D．13/6
4.
设x1、x2、x3依次是方程
，
，2x+x=2的根，则有（
）
A．x2＜x3＜x1 B．x1＜x3＜x2 C．x2＜x1＜x3 D．x3＜x2＜x1
5.
设
（n∈N），则在数列{an}的前30项中的最大项、最小项依次是 （ ）
A．a1，a30 B．a1，a9 C．a10，a9 D．a10，a30
6.
已知集合P＝{(x,y)y＝
}、Q＝{(x,y)y＝x＋b}，若P∩Q≠
，则b的取值范围是 ．
A．b<3 B．b≤3
C．－3≤b≤3 D．－3<b<3
二、填空题（A、B、C三级试题分别为2、1、1，共4小题）：
7. 若不等式m>x－1＋x＋1的解集是非空数集，那么实数m的取值范围是_________．
8.
若方程x－3ax＋2a＝0的一个根小于1，而另一根大于1，则实数a的取值范围是______．
9.
对于满足0≤p≤4的所有实数p，使不等式x＋px＞4x＋p－3成立的x的取值范围是________．
10. 若关于x的方程x－6x＋8＝a恰有两个不等实根，则实数a的取值范围是____________．
三、解答题（A、B、C三级试题分别为2、2、2，共6小题）：
11. 已知函数g(x)=lg[a(a+1)x2－(3a+1)x+3]的值域是R，求实数a的取值范围．
12. 定义域内不等式
恒成立，求实数
的取值范围．
13. 已知点A（0,1）、B（2,3）及抛物线y＝x＋mx＋2，若抛物线与线段AB相交于两点，求实数m的取值范围．
14.
当实数
在什么范围内时，方程
有两个不相等的实数根．
15. 已知二次函数f(x)=ax2+bx(a,b为常数，且a≠0)满足条件:f(x–1)=f(3–x)且方程f(x)=2x有等根．
（1）求f(x)的解析式；
（2）是否存在实数m，n(m＜n)，使f(x)定义域和值域分别为［m,n］和［4m,4n］，如果存在，求出m、n的值；如果不存在，说明理由．
16. （1）一次函数f(x)=kx+h(k≠0)，若m＜n有f(m)＞0，f(n)＞0，则对于任意x∈(m，n)都有f(x)＞0，试证明之；
（2）试用上面结论证明下面的命题：
若a，b，c∈R且a＜1，b＜1，c＜1，则ab+bc+ca＞-1
三、函数思想方法的应用参考答案
【例题】
1．D
2．B
3．
4．解析：作函数y=x2－4x+3的图象，如下图．
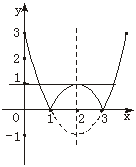
由图象知直线y=1与y=x2－4x+3的图象有三个交点，即方程x2－4x+3=1也就是方程x2－4x+3－1=0有三个不相等的实数根，因此a=1．
答案：1
5．解：设
（y1≥0）
∴ 
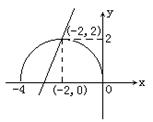
（y1≥0），它表示以（-2，0）为圆心，2为半径的上半圆．
表示和
平行或重合的直线系．分别作出y1与y2的图象，让y2作平行移动，要y1≥y2解集为{x-4≤x≤-2}，显然当且仅当直线通过点（-2，2）时符合要求，此时
∴ 
6．解：将y=3-x代入抛物线方程得：x2-（m+1）x+4=0（*）
（*）应满足条件：在[0，3]内有两个不同的实根．令f（x）=x2-（m+1）x+4．
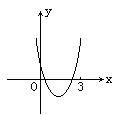由如图，则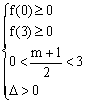
解得：3＜m≤
7．【解】问题可变成关于m的一次不等式：（x－1）m－（2x－1）<0在[-2,2] 恒成立，设f（m）＝（x－1）m－（2x－1）,
则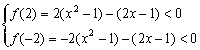 
解得x∈（
,
）
【注】 本题的关键是变换角度，以参数m作为自变量而构造函数式，不等式问题变成函数在闭区间上的值域问题．本题有别于关于x的不等式2x－1>m（x－1）的解集是[-2,2]时求m的值、关于x的不等式2x－1>m（x－1）在[-2,2]上恒成立时求m的范围．
8．【分析】当x∈（-∞,1]时f（x）＝lg有意义的函数问题，转化为1＋2＋4a>0在x∈（-∞,1]上恒成立的不等式问题．
【解】 由题设可知，不等式1＋2＋4a>0在x∈（-∞,1]上恒成立，
即：（
）
＋（）＋a>0在x∈（-∞,1]上恒成立．
设t＝（）, 则t≥，
又设g（t）＝t＋t＋a，其对称轴为t＝－
∴ t＋t＋a＝0在[,+∞）上无实根，
即 g（）＝（）＋＋a>0，得a>－
所以a的取值范围是a>－．
【注】对于不等式恒成立，引入新的参数化简了不等式后，构造二次函数利用函数的图像和单调性进行解决问题，其中也联系到了方程无解，体现了方程思想和函数思想．一般地，我们在解题中要抓住二次函数及图像、二次不等式、二次方程三者之间的紧密联系，将问题进行相互转化．
在解决不等式（）＋（）＋a>0在x∈（-∞,1]上恒成立的问题时，也可使用“分离参数法”：
设t＝（）, t≥，则有a＝－t－t∈（－∞,－
]，所以a的取值范围是a>－．其中最后得到a的范围，是利用了二次函数在某区间上值域的研究，也可属应用“函数思想”．
9．【解】 原方程变形为 
即：
设曲线y
＝（x－2） , x∈（0,3）和直线y
＝1－m，画图可知：
① 当1－m＝0时，有唯一解，m＝1;
②当1≤1－m<4时，有唯一解，即－3<m≤0,
∴ m＝1或－3<m≤0
此题也可设曲线y＝－（x－2）＋1 , x∈（0,3）和直线y＝m后画出图像求解．
【注】 一般地，方程的解、不等式的解集、函数的性质等进行讨论时，可以借助于函数的图像直观解决，简单明了．此题也可用代数方法来讨论方程的解的情况，还可用分离参数法来求（也注意结合图像分析只一个x值）．
10．解：（1）
x＜–3或x＞3．
∵f(x)定义域为［α,β］,∴α＞3
设β≥x1＞x2≥α，有
当0＜m＜1时，f(x)为减函数，当m＞1时，f(x)为增函数．
（2）若f(x)在［α,β］上的值域为［logmm(β–1),logmm(α–1)］
∵0＜m＜1, f(x)为减函数．
∴
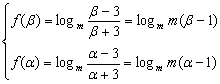
即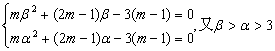
即α,β为方程mx2+(2m–1)x–3(m–1)=0的大于3的两个根
∴
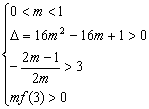∴0＜m＜
故当0＜m＜时，满足题意条件的m存在．
11．解：（读题）由主要关系：运输总成本＝每小时运输成本×时间，
（建模）有y＝（a＋bv
）
（解题）所以全程运输成本y（元）表示为速度v（千米／时）的函数关系式是：
y＝S（
＋bv），其中函数的定义域是v∈（0，c] ．
整理函数有y＝S（
＋bv）＝S（v＋
），
由函数y＝x＋
（k>0）的单调性而得：
当
<c时，则v＝时，y取最小值；
当≥c时，则v＝c时，y取最小值．
综上所述，为使全程成本y最小，当<c时，行驶速度应为v＝；当≥c时，行驶速度应为v＝c．
12．解：（1）由A直接游向B的时间
（秒）
由A经D游向B的时间
（秒）
而
，因此救生员的选择是正确的。
（2）
,则从A经C到B的时间为t,
因此点C应选沿岸边AD距D点
米处,才能使救生员从A经C到B所用的时间最短为
秒
13．已知
，g(x)=x+a
(a>0)．
（1）当a=4时，求
的最小值；
（2）当
时，不等式>1恒成立，求a的取值范围．
13．解（1）当a=4时， ＝
，当
时，即x=4时，取最小值15．
（2）>1
．
记
，比照函数
的图象的性质可知：
（1）当0<a<1时，
(x)在[1,4]上单调递增，min(x)= (1)＝a(a+1)>2,解得a<-2或a>1（舍）；
（2）当a>4时，(x)在[1,4]上单调递减，min(x)= (4)＝
，解得a>4；
（3）当
时，(x)
，解得
．
综上有：a>1．
【习题】
11．解：由题意知，应使h（x）=a（a+1）x2－（3a+1）x+3能取到一切正实数．
①a=0时，h（x）=－x+3，显然能取到一切正实数；
②a=－1时，h（x）=2x+3，也能取到一切正实数；
③a≠0且a≠－1时，∵h（x）=a（a+1）x2－（3a+1）x+3是二次函数，
∴必须有
解得
≤a＜－1或0＜a≤
．
综上所述，a的取值范围是［，－1］∪［0，］．
15．解：（1）∵方程ax2+bx=2x有等根，∴Δ=(b–2)2=0,得b=2．
由f(x–1)=f(3–x)知此函数图象的对称轴方程为x=–
=1得a=–1，故f(x)=–x2+2x．
（2）f(x)=–(x–1)2+1≤1，∴4n≤1，即n≤
而抛物线y=–x2+2x的对称轴为x=1
∴n≤时，f(x)在［m,n］上为增函数．
若满足题设条件的m,n存在，则
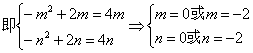
又m＜n≤,∴m=–2,n=0，这时定义域为［–2,0］，值域为［–8,0］．
由以上知满足条件的m、n存在，m=–2,n=0．
16．（1）证明：
当k＞0时，函数f(x)=kx+h在x∈R上是增函数，m＜x＜n，f(x)＞f(m)＞0；
当k＜0时，函数f(x)=kx+h在x∈R上是减函数，m＜x＜n，f(x)＞f(n)＞0
所以对于任意x∈(m，n)都有f(x)＞0成立
（2）将ab+bc+ca+1写成(b+c)a+bc+1，构造函数f(x)=(b+c)x+bc+1则f(a)=(b+c)a+bc+1
当b+c=0时，即b=-c，f(a)=bc+1=-c2+1因为c＜1，所以f(a)=-c2+1＞0
当b+c≠0时，f(x)=(b+c)x+bc+1为x的一次函数
因为b＜1，c＜1，
f(1)=b+c+bc+1=(1+b)(1+c)＞0， f(-1)=-b-c+bc+1=(1-b)(1-c)＞0
由问题(1)对于a＜1的一切值f(a)＞0，即(b+c)a+bc+1=ab+ac+bc+1＞0
说明：问题(2)的关键在于“转化”“构造”把证明ab+bc+ca＞-1转化为证明ab+bc+ca+1＞0，
由于式子ab+bc+ca+1中， a，b，c是对称的，构造函数f(x)=(b+c)x+bc+1，则f(a)=(b+c)a+bc+1，问题转化为在a＜1，b＜1，c＜1的条件下证明f(a)＞0(也可构造 f(x)=(a+c)x+ac+1，证明f(b)＞0)