高一年级上册期中数学试卷
一． 选择题（每小题5分，共50分）
1、若集合
，则
等于
（ ）
（A）｛－1,0，1,2｝ （B）｛0,1，2｝ （C）｛－1,0，1｝ （D）｛0,1｝
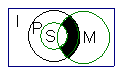
2．如图，I为全集，M、P、S是I的三个子集，则阴影部分所表示的集合是 （ ）
A．
B．
C．
D．
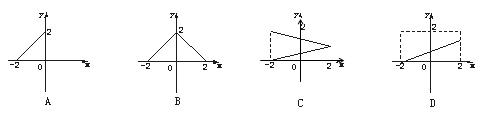
3．设M={x－2≤x≤2}，N={y0≤y≤2}，函数f（x）的定义域为M，值域为N，则f（x）的图象可以是 （ ）
4．设函数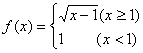
，则
=
（ ）
A．0 B．1 C．2 D．
5、函数
的定义域是
（ ）
A．
B．
C．
D．
6．函数
的值域是
（ ）
A．[0，2] B．[1，2] C．[－2，2] D．[－，]
7．函数
的图象
（ ）
A．关于x轴对称 B．关于y轴对称 C．关于原点对称 D．关于直线
对称
8、函数y=f(x)是单调函数，则方程f(x)=a （ ）
(A)至少一个解 (B)至多一个解 (C)恰一个解 (D)无穷多个解
9．已知1＜m＜n，令a=（lognm）2，b=lognm2，c=logn（lognm），则 （ ）
A.a＜b＜c B.a＜c＜b
C.b＜a＜c D.c＜a＜b
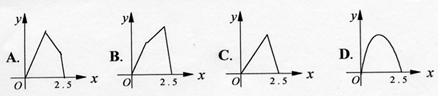
10、如图，点P在边长的1的正方形的边上运动，设M是CD边的中点，当P沿A→B→C→M运动时，以点P经过的路程
为自变量，
的面积为
，则函数
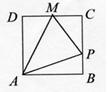的图象大致是 （ ）
二．填空题（每小题5分，共30分）
11．函数y=loga（2－ax）在［0，1］上是减函数，则a的取值范围是
12．已知
是偶函数，且定义域为
，则
，
.
13．一元二次方程
的一根比1大，另一根比－1小，则实数a的取值范围是
14．二次函数y=ax2+bx+c（x∈R）的部分对应值如下表：
| x | －3 | －2 | －1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | －4 | －6 | －6 | －4 | 0 | 6 |
则不等式ax2+bx+c＞0的解集是______________.
15．化简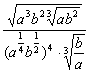
（a＞0，b＞0）的结果是___________________.
16．关于x的方程x2－4x+3－a=0有三个不相等的实数根，则实数a的值是___________________.
三．解答题（80分）
17．已知集合
①若
，求实数m的取值范围；
②若
，求实数m的取值范围。（12分）
18、(本题满分12分)某地对100户农户的生活情况作了调查，交来的统计表上称：有彩电的65户，有电冰箱的84户，二者都有的53户．
（1）问彩电与冰箱至少有一种的有几户？
（2）若二者全无的只有2户，问这一统计数字正确吗？（12分）
19． 设函数f（x）＝
（a＞b＞0），求f（x）的单调区间，并证明f（x）在其单调区间上的单调性. （12分）
20．如下图，在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点（起点）向A点（终点）移动，设P点移动的路程为x，△ABP的面积为y=f（x）.
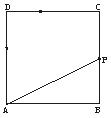
（1）求△ABP的面积与P移动的路程间的函数关系式；
（2）作出函数的图象，并根据图象求y的最大值. （14分）
21．求函数
的定义域和值域。（14分）
22．定义在R上的函数y=f（x），f（0）≠0，当x＞0时，f（x）＞1，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.
（1）求证：f（0）=1；
（2）求证：对任意的x∈R，恒有f（x）＞0；
（3）求证：f（x）是R上的增函数；
（4）若f（x）·f（2x－x2）＞1，求x的取值范围. （16分）
高一年级期中数学试卷答题纸
一.选择题（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题(每小题5分,共30分)
11. 12. 13.
14. 15. 16.
三.解答题(80分)
17.(12分)
18. (12分)
19. (12分)
20. (14分)
21. (14分)
22. (16分)
2007～2008学年度第一学期期中数学试卷
高一年级数学参考答案及评分标准
说明：
1、 本解答仅给出了一种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容对照评分标准制定相应的评分细则。
2、 评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定后续部分的给分，但不得超过该部分正确解答应得分数的一半，如果后续部分的解答有较严重的错误，就不给分。
3、 解答右端所注分数，表示考生正确做到这一步应得的累加分数。
4、 给分或扣分以1分为单位，选择题和填空题不给中间分。
一、选择题：本题考查基本知识和基本运算。每小题5分，满分50分。
1．A 2．D 3．B 4．B 5．D 6．A 7．C 8．B 9．D 10．A
二、填空题：本题考查基本知识和基本运算。每小题5分，满分30分。
11．1＜a＜2；12．
0；13．－2<a<1；14．{xx＞3或x＜－2} ； 15．
；16．a=1
三．解答题（80分）
17．已知集合
①若，求实数m的取值范围；
②若，求实数m的取值范围。
解：
…………………………2分
①
…………………………7分
②
…………………………12分
18、(本题满分12分)某地对100户农户的生活情况作了调查，交来的统计表上称：有彩电的65户，有电冰箱的84户，二者都有的53户．
（1）问彩电与冰箱至少有一种的有几户？
（2）若二者全无的只有2户，问这一统计数字正确吗？
解：（1）（文氏图法）
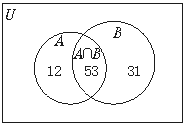
设A={有彩电的农户}，B={有冰箱的农户}，全集U={调查的100户农户}，由题可知A∩B={53户农户}．
∴彩电冰箱至少有一种的农户有96户． …………………………7分
（2）若二者全无的只有2户，加上彩电冰箱至少有一种的农户，共有98户，少于100户，故这一统计数据不正确． …………………………12分
19． 设函数f（x）＝（a＞b＞0），求f（x）的单调区间，并证明f（x）在其单调区间上的单调性.
解：函数f（x）＝的定义域为（－∞，－b）∪（－b，＋∞），
任取x1、x2∈（－∞，－b）且x1＜x2， …………………………3分
则f（x1）－f（x2）＝
－
＝
.…………………………7分
∵a－b＞0，x2－x1＞0，（x1＋b）（x2＋b）＞0，
∴f（x1）－f（x2）＞0，
即f（x）在（－∞，－b）上是减函数. …………………………10分
同理可证f（x）在（－b，＋∞）上也是减函数.
∴函数f（x）=在（－∞，－b）与（－b，＋∞）上均为减函数. ……………12分
20．如下图，在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点（起点）向A点（终点）移动，设P点移动的路程为x，△ABP的面积为y=f（x）.
（1）求△ABP的面积与P移动的路程间的函数关系式；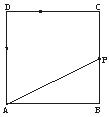
（2）作出函数的图象，并根据图象求y的最大值.
解：（1）这个函数的定义域为（0，12）.
当0＜x≤4时，S=f（x）=
·4·x=2x；
当4＜x≤8时，S=f（x）=8；
当8＜x＜12时，S=f（x）=·4·（12－x）=2（12－x）=24－2x.
∴这个函数的解析式为
f（x）=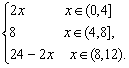
…………………………8分
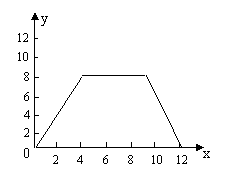
（2）其图形为
由图知，［f（x）］max=8. …………………………14分
21．求函数的定义域和值域。
解：由有意义得
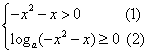
由（1）得
，则
由（2）得，当
时，有
，则
无解；
当
时，有。
则当时，
；当时，
22．定义在R上的函数y=f（x），f（0）≠0，当x＞0时，f（x）＞1，且对任意的a、b∈R，有f（a+b）=f（a）·f（b）.
（1）求证：f（0）=1；
（2）求证：对任意的x∈R，恒有f（x）＞0；
（3）求证：f（x）是R上的增函数；
（4）若f（x）·f（2x－x2）＞1，求x的取值范围.
解：（1）证明：令a=b=0，则f（0）=f 2（0）.
又f（0）≠0，∴f（0）=1. …………………………2分
（2）证明：当x＜0时，－x＞0，
∴f（0）=f（x）·f（－x）=1.
∴f（－x）=
＞0.又x≥0时f（x）≥1＞0，
∴x∈R时，恒有f（x）＞0. …………………………6分
（3）证明：设x1＜x2，则x2－x1＞0.
∴f（x2）=f（x2－x1+x1）=f（x2－x1）·f（x1）.
∵x2－x1＞0，∴f（x2－x1）＞1.
又f（x1）＞0，∴f（x2－x1）·f（x1）＞f（x1）.
∴f（x2）＞f（x1）.∴f（x）是R上的增函数.…………………………10分
（4）解：由f（x）·f（2x－x2）＞1，f（0）=1得f（3x－x2）＞f（0）.又f（x）是R上的增函数，
∴3x－x2＞0.∴0＜x＜3. …………………………16分