高一年级数学三角函数周末练习（1）
（方善泽）
知识要点
1.终边相同的角：与α角终边相同的角的集合（连同α角在内），可以记为{
＝k·360＋α，k∈Z}。
2.象限角：顶点在原点，始边与x轴非负半轴重合，则终边落在第几象限，就称这个角是第几象限的角。
3.各象限角的集合及各轴线角的集合表示。
4.区间角、区间角的集合： 角的量数在某个确定的区间内（上），这角就叫做某确定区间的角．由若干个区间构成的集合称为区间角的集合．
5.弧度与角度互换公式：1rad＝
°≈57.30°=57°18ˊ． 1°＝
≈0.01745（rad）
6.弧长公式：
. 扇形面积公式：
7.三角函数：设
是一个任意角，在的终边上任取（异于原点的）一点P（x,y）P与原点的距离为r，则 
； 
； 
；
8.三角函数在各象限的符号：（一全二正弦，三切四余弦）
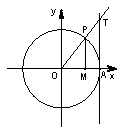
9.三角函数线： 正弦线：MP; 余弦线：OM; 正切线： AT.
基本练习
一、选择题
1. 下列说法正确的是 （ ）
A 第一象限角一定不是负角 B 小于90o的角一定是锐角
C 钝角一定是第二象限角 D 终边相同的角一定相等
2.
与
终边相同的角可以是下列中的 （
）
A 
B
C
D
3.
已知角
则符合条件的最大负角为 （
）
A 
B
C
D
4.
化为弧度是 （
）
A 
B 
C 
D 
5.
则的终边在 （
）
A 第一象限 B 第二象限 C 第三象限 D 第四象限
6. 将时针拨慢10分钟，则分针转过的弧度是 （ ）
A 
B 
C 
D 
7. 圆的半径是6cm，则15o的圆心角与圆弧所对的扇形面积是 （ ）
A 
B
C
D
8.
集合
，
，则 （
）
A、
B、
C、
D、
9.
设是第三、四象限角，
，则
的取值范围是 （
）
A、（－1,1） B、（－1，
C、（－1，
D、
10. 如果
是第一象限角，那么恒有 （
）
A、
＞0 B、
＜1 C、＞
D、＜
二、填空题
11. 设
，将
表示成
的形式是
。
12. 与角
的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。
13. 若是第二象限角，则
是第_____象限角，2的范围是__________，
是第_____象限角。
14. 已知角的终边经过点P(5，－12)，则
的值为＿＿。
15. 在半径为R的圆中，
的中心角所对的弧长为＿＿＿，面积为
的扇形的中心角等于＿＿＿弧度。
16. 的终边与
的终边关于直线
对称，则＝＿＿＿＿＿＿。
17. 函数
的值域是＿＿＿＿＿＿＿。
18. 时钟经过40分钟，时针转过的角度是 。
19. 角是第二象限角，则
是第 象限角；
是第 象限角；
是第 象限角。
20. 一个扇形的面积是
，周长为
，则圆心角的弧度数为 ，弦长为 。
三、解答题
21. 写出与
终边相同的角的集合S，并把S中适合
的元素
写出来。
22. 已知扇形的周长为30cm，当它的半径和圆心角个取什么值时，才能使扇形的面积最大？最大面积是多少？
23. 若
，试判断
的符号。
24. 已知角的顶点在原点，始边与
轴的非负半轴重合，终边为射线
。
（1）求
的值；
（2）若角的终边在直线
上，求的值。
25. 已知一半径为R的扇形，它的周长等于所在圆的周长，那么扇形的中心角是多少弧度？合多少度？扇形的面积是多少？
26. 已知角的终边经过点P(－
)（
），且
，求
的值。
27. 设是第二象限角，试比较，，的大小.
28. A是以O为圆心，半径为1cm的圆周上一定点，动点P从A出发，以每分钟5圈的速度逆时针旋转，
的面积
与旋转时间
秒的函数关系为
，求的解析式。
深圳实验学校高中部高一年级周末练习（1）
三角函数参考答案
1～10.CCABC;ABCCBA;
11.
；
12.
；
；
13.第一或第三；
；第四；
14.
15.
；4；
16.
；
17.｛－2,0，4｝；
18.
；
19.Ⅳ、Ⅲ、Ⅰ；
20．2rad；
；
21.
；
；
22.
、圆心角为2rad时，扇形面积最大，最大值为
；
23.＜0
24.（1）
（2）
25.
弧度；
度约为
；
26.当
时，
，当
时，
27.当
第Ⅰ象限时，＜＜；
当第Ⅲ象限时，＜＜
28.