高一数学模块一综合练习
 班级____________ 姓名____________
班级____________ 姓名____________
Mathematics in Hand:(掌握数学)
张开右手,你将看到你的掌纹。有人称它是命运的密语,其实它是我们熟悉的指数函数、对数函数和幂函数的图像。它每天都在我们的掌中。掌握数学也就是掌握自己的命运!
1.集合![]() ,
,![]() 则
则![]() 为(
)
为(
)
A.![]() B.{0,1} C.{1,2} D.
B.{0,1} C.{1,2} D.![]()
2.已知集合![]() ,
,![]() 则
则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设![]() ,
,![]() ,
,![]() ,则(
).
,则(
).
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.已知函数![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() 时,
时,![]() ,则
,则![]() 在R上的解析式为 (
) A.
在R上的解析式为 (
) A.
![]() B.
B.![]() C.
C.![]() D.
D. ![]()
5.要使![]() 的图象不经过第二象限,则t的取值范围为
(
)
的图象不经过第二象限,则t的取值范围为
(
)
A. ![]() B.
B.
![]() C.
C.![]() D.
D. ![]()
6.已知函数![]() 在区间
在区间![]() 上是
上是![]() 的减函数,则
的减函数,则![]() 的取值范围是(
)
的取值范围是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是 ( )
的取值范围是 ( )
A
![]() B
B ![]() C
C ![]() D
D ![]()
8.设![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值之差为
上的最大值与最小值之差为![]() ,则
,则![]() ( ) www.xkb123.com
( ) www.xkb123.com
A.![]() B.2 C.
B.2 C.![]() D.4
D.4
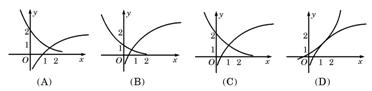
9. 函数![]() 与
与![]() 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
10.定义在R上的偶函数![]() 满足
满足![]() ,且当
,且当![]()
![]() 时
时![]() ,
,
则![]() 等于 (
) A.
等于 (
) A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
11.根据表格中的数据,可以断定方程![]() 的一个根所在的区间是( ).
的一个根所在的区间是( ).
|
| -1 | 0 | 1 | 2 | 3 |
|
| 0.37 | 1 | 2.72 | 7.39 | 20.09 |
|
| 1 | 2 | 3 | 4 | 5 |
A. (-1,0) B. (0,1) C. (1,2) D. (2,3)
12.下表显示出函数值![]() 随自变量
随自变量![]() 变化的一组数据,由此判断它最可能的函数模型是( ).
变化的一组数据,由此判断它最可能的函数模型是( ).
| x | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 15 | 17 | 19 | 21 | 23 | 25 | 27 |
A.一次函数模型 B.二次函数模型 C.指数函数模型 D.对数函数模型
13.若![]() ,
,![]() ,则
,则![]() .
.
14.![]() =________
=________
15.已知函数![]() 同时满足:(1)定义域为
同时满足:(1)定义域为![]() 且
且![]() 恒成立;
恒成立;
(2)对任意正实数![]() ,若
,若![]() 有
有![]() ,且
,且![]() .试写出符合条件的函数
.试写出符合条件的函数![]() 的一个解析式
的一个解析式
16.给出下面四个条件:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,能使函数
,能使函数![]() 为单调减函数的是
.
为单调减函数的是
.
17.已知集合![]() ,集合
,集合![]()
(1)对于区间![]() ,定义此区间的“长度”为
,定义此区间的“长度”为![]() ,若A的区间“长度”为3,试求实数
,若A的区间“长度”为3,试求实数![]() 的值。
的值。
(2)若![]()
![]()
![]() ,试求实数
,试求实数![]() 的取值范围。
的取值范围。
18.试用定义讨论并证明函数![]() 在
在![]() 上的单调性.
上的单调性.
19.已知二次函数![]()
(1)
若函数在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2) 问:是否存在常数![]() ,使得当
,使得当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
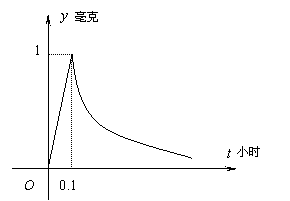
20.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,![]() 与
与![]() 的函数关系式为
的函数关系式为![]() (
(![]() 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题:
(1)写出从药物释放开始,每立方米空气中的含药量![]() (毫克)与时间
(毫克)与时间![]() (小时)之间的函数关系式;
(小时)之间的函数关系式;
 (2)据测定,当空气中每立方米的含药量降低到
(2)据测定,当空气中每立方米的含药量降低到![]() 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
21.已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() ,使得
,使得![]() 成立.
成立.
(1)函数![]() 是否属于集合
是否属于集合![]() ?说明理由; (2)设函数
?说明理由; (2)设函数![]() ,证明:
,证明:![]() .
.
22.已知定义域为![]() 的函数
的函数![]() 是奇函数。 (1)求
是奇函数。 (1)求![]() 的值;
的值;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
参考答案:
DCACA BCDCD CA
13. 3 14. ![]() 15.
15. ![]() 等 16. ①④
等 16. ①④
17.(1)![]() (2)
(2)![]()
18.![]() 时递增,
时递增,![]() 时递减
时递减
19.(1)![]() (2)9
(2)9
20.(1)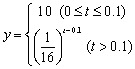 (2)
(2)![]()
21.(1)不属于
(2)转化为研究![]() 的零点问题
的零点问题
22.(1) ![]() (2)
(2) ![]()